 ⋅ 2n such that for every x
⋅ 2n such that for every x  Sn,
it holds that
Sn,
it holds that
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 461b: Foundations of Cryptography | Handout #3 | |
| Professor M. J. Fischer | February 12, 2009 | |
Three Proofs of a Simple Lemma
We give three proofs of a claim from the textbook:
Claim 2.5.2.1: There exists a set Sn ⊆{0,1}n of cardinality at least  ⋅ 2n such that for every x
⋅ 2n such that for every x  Sn,
it holds that
Sn,
it holds that
![s(x) d=f Pr[G (f(x),Rn ) = b(x,Rn )] ≥ 1-+ ε(n)
2 2](ho031x.png)
This claim is stated in a rather awkward way. Instead of existentially quantifying Sn, it is simpler to just define it in terms of s(⋅), namely, Definition:
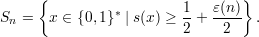
Then the claim we are trying to prove follows from the slightly stronger
Lemma 1
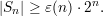
We will need one further fact about s(⋅). Fact
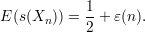
This follows immediately from the definition of ε(n) given in the book.
We give three proofs of the lemma—one algebraic, one geometric, and one using Markov’s inequality.
The algebraic proof relies on the definition of expectation, namely, that
![∑ ∑
E(s(Xn )) = Pr[Xn = x]⋅s(x) = 2-n s(x).
x x](ho035x.png)
The key idea is to split the sum into two parts, those terms where x  Sn and those terms where x ⁄
Sn and those terms where x ⁄ Sn.
Towards this end, define Sn = {0,1}*- Sn. We then have
Sn.
Towards this end, define Sn = {0,1}*- Sn. We then have
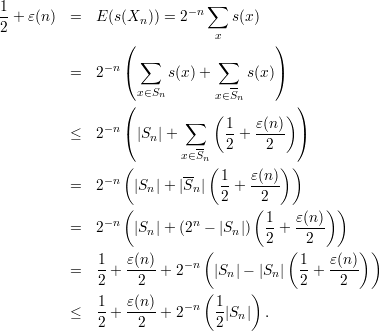
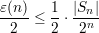
from which it follows that
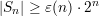
as desired.
The geometric proof is based on an analysis of the graph of the function s(x). Assume that the domain of s(⋅) has been ordered so as to make s(⋅) non-decreasing. Then the graph of s(⋅) looks like the diagram of Figure 1. I have drawn a solid horizontal line at y = 1∕2 + ε(n) = E(s(Xn)). This is the average value of s(⋅) over its domain. Hence, the area above the curve and below this line (regions A and B in the diagram) is the same as the area above the line and below the curve (region C in the diagram).
I have drawn a second horizontal line at y = 1∕2 + ε(n)∕2. This is the defining threshold for the set Sn. I have drawn a vertical dashed line through the point where it intersects the curve. Values of x to the right of this line are in Sn, and those to the left are not. The goal is to prove that the line cannot be too far to the right (so that Sn isn’t too small).
The proof is now fairly straightforward. First of all, as noted before, we have
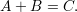
Clearly, region A includes the skinny rectangle between the two horizontal lines. It has height ε(n)∕2 and width 2n -|Sn|. Hence,
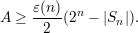
Region C is entirely contained within the upper right hand rectangle of height 1∕2 -ε(n) and width |Sn|. Hence,
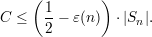
Combining these facts, we have
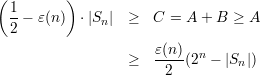
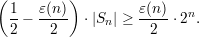
Solving for |Sn|, we get
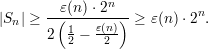
Recall Markov’s inequality:
![E-(X-)
Pr[X ≥ v] ≤ v .](ho0316x.png)
The proof using Markov’s inequality applies the inequality to the random variable 1 - s(Xn) to obtain
![[ 1 ε(n)] E (1- s(Xn ))
Pr 1 - s(Xn) ≥ --- ---- ≤ ---1---ε(n)---.
2 2 2 - -2-](ho0317x.png)
It uses the fact that
![[ ]
1- ε(n) |Sn|
Pr s(Xn ) ≥ 2 + 2 = Pr[Xn ∈ Sn] = 2n .](ho0318x.png)
Hence, to prove our lemma, we establish a lower bound on this quantity.
The calculation is an exercise in change of signs and negation of events.
![[ ] [ ]
Pr s(Xn ) ≥ 1-+ ε(n) = 1- Pr s(Xn ) < 1-+ ε(n-)
2 2 2 2
[ 1 ε(n)]
= 1- Pr 1 - s(Xn ) > 2-- -2-- .](ho0319x.png)
![[ ]
1- ε(n) E-(1--s(Xn-))
1 - Pr 1- s(Xn ) > 2 - 2 ≥ 1 - 1 ε(n)
2 - 2
1 - (1 + ε(n ))
= 1 - -----2-ε(n)---
12 - -2-
ε(n)
= 1--ε(n)-
≥ ε(n).](ho0320x.png)
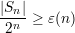
and the lemma follows.