YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE

CPSC 461b: Foundations of Cryptography Notes 6 (rev. 1)
Professor M. J. Fischer January 29, 2009

Lecture Notes 6

18 Goldreich’s “Toy Example”

18.1 Motivation

The goal of the next two lectures is to prove:

Theorem 1 Weakly one-way functions exist iff strongly one-way functions exist.

Proof: [Sketch] The backwards direction is trivial since every strongly one-way function is also weakly one-way.

For the forwards direction, we construct a strongly one-way function g from a weakly one-way function f. The construction is straightforward — g just evaluates f on a large number t(n) of arguments and concatenates together the results. That is, g(x) = (f(x1),…,f(xt(n))), where x = x1,…,xt(n) is viewed as consisting of t(n) length-n strings, and t(n) is a suitably-chosen polynomial. Intuitively, g(x) is hard to invert if f(xi) is hard to invert for at least one i. __

Proving that this intuition correct requires careful attention to detail and a substantial amount of probabilistic reasoning. The full proof will be presented in the next lecture.

18.2 Some key ideas

Because of the complexity of the careful proof of theorem 1, it is useful to look first at a careful proof of a simpler theorem that illustrates many, but not all, of the ideas that go into the full proof.

We introduce some terminology to simplify discussions of the difficulty of inverting functions. We write A′ inverts f(x) to denote the event A′(x,I|x|) ∈ f-1(f(x)), and we write A′ fails on f(x) to denote its complement . With this shorthand, it follows that

′ ′ n - 1 P r[A inverts f (Un )] = P r[A (Un, 1 ) ∈ f (f (Un ))].

Definition: Let ρ ∈ [0,1]. A function f is deterministic ρ-one-way if for all deterministic polynomial time algorithms A′ and all sufficiently large n,

′ P r[A fails on f(Un)] ≥ ρ (n ).

Theorem 2 (Proposition 2.3.3 in text) Suppose f is deterministic 1/3-one-way. Define

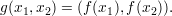
g(x1,x2) = (f(x1),f(x2)).

Then g is deterministic 0.55-one-way.

(Note that 0.55 < 1 - (2∕3)2.)

Proof: Suppose g is not 0.55-one-way. Then there exists a polynomial time algorithm B′ that inverts g(U2n) with success probability > 1 - 0.55 = 0.45 for ∞-many n. Consider such an n and let N = 2n.

Define the N ×N matrix μ by μ(x1,x2) = 1 if B′ succeeds on input g(x1,x2) = (f(x1),f(x2)) and μ(x1,x2) = 0 otherwise, where |x1| = |x2| = n. Then

P r[B ′(U ) inverts g(U )] = # 1’s in μ-> 0.45. 2n 2n N 2
(1)

If B′ operated independently on each component of the pair (f(Un),f(Un)), then μ would have a simple structure. Namely, one could define

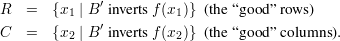
′ R = {x1 | B inverts f(x1)} (the “goo d” rows) C = {x2 | B′ inverts f(x2)} (the “goo d” columns).
It would then follow that B′ succeeds in inverting g(x1,x2) iff it succeeds on both f(x1) and f(x2), so μ(x1,x2) = 1 iff x1 ∈ R and x2 ∈ C. By assumption f is deterministic 1/3-one-way, so |R|,|C|≤ (2∕3)N. Hence,
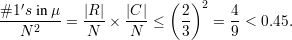
( ) #1-′s in μ |R-| |C-| 2- 2 4- N 2 = N × N ≤ 3 = 9 < 0.45.

which would contradict inequality 1.

However, B′ does not necessarily have to operate in such a way. Perhaps B′ can somehow “solve” the simultaneous equations

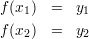
f(x ) = y 1 1 f(x2) = y2
for x1 and x2 given y1 and y2 with higher success probability that it can achieve by solving the two equations independently. We don’t know if this can be done, but we can’t rule it out, either. Hence, we need a more sophisticated argument to derive our contradiction.

Call a row (column) of μ good if at least 0.1% of the entries in it are 1 and bad otherwise.

Claim 1 The fraction of good rows (columns) in μ is ≤ 66.8%.

Proof: [of claim] Suppose the fraction of good rows > 66.8%. Consider the algorithm I′ for inverting f on input y:

  1. Choose x2 uniformly at random in {0,1}n.
  2. Run B′(y,f(x2)) = (x′,x′′).
  3. If f(′x) = y, halt with output x′, and announce “success”.

Now, algorithm A′(y) runs I′(y) repeatedly for 10,000 times. If any of the runs of I′(y) succeeds, then A′ succeeds and gives the same output as I′; otherwise, A′ fails.

For every good x1,

P r[I′ fails on f (x1 )] ≤ 1- 0.001 = 0.999 .

Hence,

′ 10,000 P r[A fails on f(x1)] ≤ 0.999 < 0.001

so

P r[A ′ inverts f(x1)] > 0.999 .

Thus, the overall success probability of A′(f(Un)) is at least

P r[Un is goo d]⋅Pr[A′(Un) inverts f(Un) | Un is good] 2 > 0.668 × 0.999 > --. 3
This contradicts the assumption that f is deterministic 1∕3-one-way. __

To finish the proof of the theorem, we conclude from Claim 1 that there are at most (0.668N)2 1’s in the intersection of the good rows and good columns. The number of 1’s in each bad row and bad column is less than 0.001N. Hence,

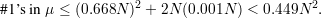
#1’s in μ ≤ (0.668N )2 + 2N (0.001N ) < 0.449N 2.

This contradicts inequality 1 and completes the proof. __