YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 461b: Foundations of Cryptography | Notes 9 (rev. 2) | |
| Professor M. J. Fischer | February 10, 2009 | |
Lecture Notes 9
We continue the proof of Lemma 3 of section 21. Recall that f is a strongly one-way and length preserving function, and that
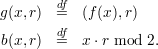
Assume to the contrary that b is not a hard core for g. Then there exists a p.p.t. algorithm G that predicts b with non-negligible advantage εG(n). Thus, there is a polynomial p(⋅) such that
![Pr[G(f (U ),X ) = b(U ,X )] ≥ 1-+--1-
n n n n 2 p(n)](ln091x.png) | (1) |
for all n in an infinite set N.
To complete the proof of Lemma 3, we will do two things:
 at
inverting f on length n inputs for all sufficiently large n in the infinite set N. This contradicts
the assumption that f is strongly one-way.
at
inverting f on length n inputs for all sufficiently large n in the infinite set N. This contradicts
the assumption that f is strongly one-way.We construct A now and defer the analysis of its success probability to the next lecture.
How can G help us to invert f? A priori it doesn’t seem to be much help to have a predictor for only a single predicate when our algorithm A is supposed to correctly output a length-n string in f-1(y). It’s not at all obvious how to use G, and several tricks are involved.
Using b to extract bits of x: Let ei be the unit vector with a 1-bit in position i and 0’s elsewhere. As before, we treat strings in {0,1}* as bit-vectors, so xi is the ith bit of x. It follows from the definition of Boolean dot product that b(x,ei) = x ⋅ ei mod 2 = xi.
Fact
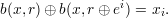 | (2) |
This follows because
Taking s = r ⊕ ei, equation 3 gives
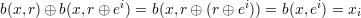 | (4) |
as desired.
First idea for A: For each i = 1,…,n, use G to guess b(x,r) and b(x,r ⊕ei) for random r, then use equation 4 to guess xi, i.e., guess xi = G(y,r) ⊕G(y,r ⊕ei). Repeat this procedure to obtain polynomially many guesses of xi and choose the majority value. Return x = x1…xn as the guess for f-1(y).
If G is correct about b on both calls, then xi is correct. As long the probability that both calls on G are
correct is greater than 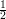 +
+ 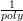 , repetition will amplify this probability to be sufficiently close to 1
so that the probability of all n bits of x being correct is also close to 1. Unfortunately, this
is only the case when G’s success probability is
, repetition will amplify this probability to be sufficiently close to 1
so that the probability of all n bits of x being correct is also close to 1. Unfortunately, this
is only the case when G’s success probability is 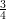 +
+ 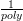 , that is, its advantage is a little bit
greater than
, that is, its advantage is a little bit
greater than 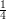 . All we know about our G is that it satisfies inequality 1, so its advantage is only
. All we know about our G is that it satisfies inequality 1, so its advantage is only
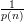 .
.
Second idea for A:
Same as first idea, except instead of using G to guess b(x,r), we just use a random bit
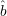 (r). Thus, we guess that xi =
(r). Thus, we guess that xi = 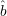 (r) ⊕ G(y,r ⊕ ei). This of course doesn’t work since the
probability of being correct is exactly
(r) ⊕ G(y,r ⊕ ei). This of course doesn’t work since the
probability of being correct is exactly 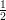 and we get no advantage. But if we somehow had an
oracle that would give us the correct value for
and we get no advantage. But if we somehow had an
oracle that would give us the correct value for 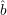 (r) = b(x,r), then this idea would indeed
work since then the advantage at guessing xi would be the same as G’s advantage at guessing
b.
(r) = b(x,r), then this idea would indeed
work since then the advantage at guessing xi would be the same as G’s advantage at guessing
b.
Third idea for A:
We generate a small (O(log n)-sized) set of random strings R0 and corresponding guesses for 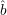 (r) for
each r
(r) for
each r  R0. From R0, we deterministically generate a polynomial set of strings R and corresponding
values for
R0. From R0, we deterministically generate a polynomial set of strings R and corresponding
values for 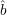 (r), r
(r), r  R. By the way the construction will work, if
R. By the way the construction will work, if 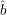 (r) is correct for all r
(r) is correct for all r  R0, then
R0, then 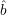 (r) is
correct for all r
(r) is
correct for all r  R. Since the number of strings in R0 for which we require correct guesses is only
O(log n), it follows that the probability of all O(log n) guesses being correct is at least
R. Since the number of strings in R0 for which we require correct guesses is only
O(log n), it follows that the probability of all O(log n) guesses being correct is at least 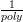 since
2O(log n) = poly(n).
since
2O(log n) = poly(n).
The strings in R are uniformly distributed over {0,1}n, but they are only pairwise independent. However, this turns out to be sufficient for the construction to work.
How to generate R0 and R: Let ℓ = ⌈log 2(2n ⋅ p(n)2 + 1)⌉.
 {0,1}n uniformly and independently. Select σ1,…,σℓ
{0,1}n uniformly and independently. Select σ1,…,σℓ  {0,1} uniformly
and independently. Let R0 = {s1,…sℓ} and
{0,1} uniformly
and independently. Let R0 = {s1,…sℓ} and 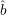 (si) = σi, i = 1,…,ℓ.
(si) = σi, i = 1,…,ℓ.
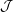 be the family of non-empty subsets of {1,2,…,ℓ}. For all sets J
be the family of non-empty subsets of {1,2,…,ℓ}. For all sets J 
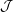 , compute
, compute
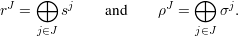
Let R = {rJ∣J 
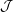 }, and
}, and 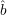 (rJ) = ρJ for all J
(rJ) = ρJ for all J 
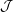 .
.
Note that r{i} = si and ρ{i} = σi, so indeed R ⊇ R0.
Fact If b(x,sj) = σj for all j  {1,…,ℓ}, then b(x,rJ) = ρJ for all J
{1,…,ℓ}, then b(x,rJ) = ρJ for all J 
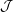 .
.
This follows because
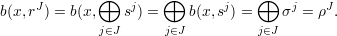
 {1,…,ℓ}, and the final equality is from the definition of
ρJ.
{1,…,ℓ}, and the final equality is from the definition of
ρJ.
Here is the complete algorithm for A. On input y, let n = |y| and ℓ = ⌈log 2(2n ⋅ p(n)2 + 1)⌉.
 {0,1}n and σ1,…,σℓ
{0,1}n and σ1,…,σℓ  {0,1}.
{0,1}.
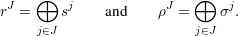
 {1,…,n}, for all non-empty J ⊆{1,…,ℓ}, compute
{1,…,n}, for all non-empty J ⊆{1,…,ℓ}, compute
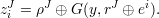
 {1,…,n}, let zi = majorityJ{ziJ}.
{1,…,n}, let zi = majorityJ{ziJ}.