12 Probabilistic analysis of a simplified Caeser cipher

To make the ideas from the previous lecture concrete, we work through a probabilistic analysis of a simplified version of the Caeser cipher restricted to a 3-letter alphabet, so 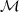= = = {0,1,2}, E_k(m) = (m + k) mod 3, and D_k(m) = (m - k) mod 3.

Assume for starters that the message distribution is given in Figure 1.

Figure 1: A priori message probabilities.

Because the keys are always chosen uniformly, each key has probability 1/3. Hence, we obtain the joint probability distribution shown in Figure 2.

Figure 2: Joint probability distribution.

Next, we calculate the conditional probability distribution prob[m = 1 ∣ c = 2]. To do this, we consider the pairs (m,k) in our joint sample space and compute c = E_k(m) for each. The diagram below shows, the result, where each point is labeled by a triple (m,k,c), and those points for which c = 2 are shown in bold type in Figure 3.

Figure 3: Sample space.

The probability that c = 2 is the sum of these probabilities corresponding to the bold face points, i.e., prob[c = 2] = 1∕6 + 1∕9 + 1∕18 = 6∕18 = 1∕3. The only one of these points for which m = 1 is (1,1,2), and it’s probability is 1∕9, so prob[m = 1 ∧ c = 2] = 1∕9. Hence,

Hence, our simplified Caeser cipher is information-theoretically secure.

Now let’s make a minor change in the cipher and see what happens. The only change is that we reduce the key space to = {0,1}. The a priori message distribution is still given by Figure 1, but the joint probability distribution changes as does the sample space as shown in Figures 4 and 5.

Figure 4: Joint probability distribution when = {0,1}.

Figure 5: Sample space when = {0,1}.

Now, prob[c = 2] = 1∕6 + 1∕12 = 3∕12 = 1∕4, and prob[m = 1 ∧ c = 2] = 1∕6. Hence,

While the a priori probability that m = 1 is still the same as it was before—1/3, the conditional probability given c = 2 is now double what it was. Indeed, there are now only two possibilities for m once Eve sees c = 2. Either m = 1 (and k = 1) or m = 2 (and k = 0). It is no longer possible that m = 0 given that c = 2. Hence, Eve narrows the possibilities for m to the set {1,2}, and her probabilistic knowledge of m changes from the initial distribution (1∕2,1∕3,1∕6) to the new distribution (2∕3,1∕3). She has learned at lot about m indeed, even without finding it exactly!

13 Perfect secrecy

In Section 12, we saw how a seemingly minor change in a cryptosystem changed it from one that had perfect secrecy to one that leaked a considerable amount of information to Eve. Perfect secrecy, while perhaps difficult to obtain, might seem like the ideal that one should strive for. We make two observations to show that even a scheme with perfect secrecy is not without defects and must still be used carefully.

First of all, our simplified Caeser cipher succumbs immediately to a known plaintext attack, since if one knows even a single plaintext-ciphertext pair (m₁,c₁), one can easily solve the equation c₁ = E_k(m₁) = (m₁ + k) mod 3 to find the key k = (c₁ - m₁) mod 3. Hence, any subsequent ciphertext c = E_k(m) is immediately decrypted using D_k() and the system is completely broken.

Second, a system with perfect secrecy can be subject to a modification attack whereby an attacker who can both read and alter message en route can modify the contents of a message in specific semantically-meaningful ways even though he has no idea what the message actually is. We refer to such an active attacker as “Mallory”, and we call such an attack a man-in-the-middle attack.

Here’s what Mallory could do to the one-letter Caeser cipher (where we now return to the original version that works over the full 26-letter alphabet). Suppose Alice sends c to Bob. Mallory intercepts it and changes c to (c + 5) mod 26. Even though he doesn’t know the key and cannot read m, he knows that his change will alter m in a similar way, changing m to (m + 5) mod 26. Why? Let’s do the calculations, where all arithmetic is done modulo 26:

Depending on the application, this could be a devastating attack. Suppose Alice were a financial institution that was making a direct deposit of m thousand dollars to Mallory’s bank account at the Bob bank. By this attack, Mallory could get an extra 5 thousand dollars put into his account each month.

For another application, note that the English vowels are all represented by even numbers in our encoding scheme where we number the letters beginning with 0. Hence, A = 0, E = 4, I = 8, O = 14, and U = 20. Hence, if m is a vowel, then the altered message m′ is guaranteed to not be a vowel. Suppose Alice were a general sending an order to a field commander whether or not to attack. If an attack is to her advantage, she orders an attack by sending a vowel; otherwise, she withholds the attack by sending a consonant. She thinks she is adding yet another layer of security by encoding the attack bit in such a non-obvious way. However, Mallory’s c + 5 transformation changes every attack message to “don’t attack” (and some “don’t attack messages to “attack”). This effectively prevents Alice from attacking in those situations where she could win. The fact that she was using a cryposystem for which perfect secrecy is known did not protect her.

This illustrates once again that the security of a system in practice depends critically on the kinds of attacks available to an attacker. In this case, the cryptosystem that is provably perfectly secure against a passive eavesdropper failed miserably against an active attacker.

14 One-time pad

Before we leave the topic of perfect secrecy, I want to present a well-known information-theoretically secure cryptosystem known as a one-time pad. This is important, both because it is sometimes used in practice, and also because it is the basis for many stream ciphers, where the truly random key is replaced by a pseudo-random bit string.

A one-time pad is a simple information-theoretically secure cryptosystem based on the bitwise exclusive-or operator (XOR), which we write as ⊕. Recall for Boolean values x and y that x ⊕ y is true when exactly one of x and y is true, but is false if x and y are either both false or both true. Exclusive-or is therefore equivalent to sum modulo two, when true is represented by 1 and false by 0. In symbols,

With a one-time pad, the plaintext, ciphertext, and key are all assumed to be binary strings of the same length. The encryption function is E_k(m) = k ⊕ m, where ⊕ is applied componentwise to corresponding bits of k and m. It’s a basic fact of mod 2 addition that addition and subtraction are the same. This implies that E_k is its own inverse; hence D_k(c) = E_k(c) is the decryption function.

Like the one-letter Caeser cipher, the simple XOR cryptosystem has the property that for every ciphertext string c and every plaintext m, there is exactly one key k such that E_k(m) = c (namely, m ⊕ c). Hence, every ciphertext is equally likely no matter what m is, so the one-time pad is information-theoretically secure.

The simple XOR cryptosystem would seem to be the perfect cryptosystem. It works for messages of any length (by choosing a key of the same length). It is simple, easy to encrypt and decrypt, and information-theoretically secure. In fact, it is sometimes used for highly sensitive data. However, it suffers from two major weaknesses that make it not so useful in practice:

1. The key k must be as long as the message to be encrypted. Key management and key distribution are both difficult problems which we will be discussing later in the course. The longer the keys, the more difficult these problems become.
2. The same key must never be used more than once. (Hence the term “one-time”.) The reason is that the simple XOR cryptosystem immediately succumbs to a known plaintext attack. If Eve knows just one plaintext-ciphertext pair (m₁,c₁), then she can easily compute k = m₁ ⊕ c₁, totally breaking the system and allowing her to decrypt all future messages sent with that key. Even in a ciphertext-only situation, if Eve has two ciphertexts c₁ and c₂ encrypted by the same key k, she can gain significant partial information about the corresponding plaintexts m₁ and m₂. In particular, she can compute m₁ ⊕ m₂, since

   That information, together with other information she might have about the likely content of the messages, may be enough for her to seriously compromise the secrecy of the data.

15 Security of the Caeser cipher

We return now to the full Caeser cipher, extended to encrypt string of letters, not just single letters. Recall that if m is an r-letter message m₁…m_r, then

is an r-letter ciphertext c₁…c_r, and

That is, we extend the basic 1-letter Caeser cipher by applying it repeatedly to each letter of the message, using the same key each time.

Although the Caeser cipher is not practical because of its small key space, many practical ciphers share the basic Caeser cipher’s property that they are build to work only on fixed-sized blocks of data (typically bitstrings of some convenient length such as 64 or 128). To send longer messages, the cipher is used repeatedly according to some rule. The simplest is to break the long message into blocks and encrypt each block separately, as we’re doing in the full Caeser cipher. Using a block cipher in this way is called “Electronic Code Book” mode, or ECB.

Consider now the problem of breaking the Caeser cipher. Suppose you intercept the ciphertext JXQ. You quickly discover that E₃(GUN) = JXQ. But can you conclude that k = 3 and GUN is the corresponding plaintext? Upon further investigation, you discover that E₂₃(MAT) = JXQ. So now you are in a quandary. You have two plausible decryptions and no way to tell for sure which is correct. Have you broken the system or haven’t you? According to the “definition” above, you haven’t since you haven’t found the plaintext with certainty. But you’ve certainly inflicted serious damage. You’ve reduced the possible set of 3-letter words that the message might have been down to a small set of possibilities. In many contexts, this is nearly as good as having completely broken the system. This suggests that a formal definition of security must take into account the possibility of “partially breaking” a system, as we did here.

The longer the message, the more likely that only one key will lead to a sensible message. For example, if the ciphertext were “EXB JXQ”, you would know that k = 3, since D₃(EXB JXQ) = BUY GUN, whereas D₂₃(EXB JXQ) = HAE MAT is nonsense.

Thus, we see that the Caeser cipher can be information-theoretically secure when r = 1, but for longer r it is only partially secure or completely breakable, depending on the length of the message to which it is applied and the redundancy present in that message.¹

16 Brute force attacks

A brute force attack is one that tries all possible keys k. For each k, Eve computes m_k = D_k(c) and tests if m_k is meaningful. If so, then m_k is a plausible decryption of c. If exactly one m_k is found that is meaningful, then Eve knows that m_k = m.

Given long enough messages, the Caeser cipher is easily broken by brute force—one simply tries all 26 possible keys and sees which leads to a sensible plaintext. The Caeser cipher succumbs because the key space is so small.

With modern computers, it is quite feasible for an attacker to try millions (~ 2²⁰) or billions (~ 2³⁰) of keys. Of course, the attacker also needs some automated test to determine when she has a likely candidate for the real key, but such tests are often easy to produce given a little knowledge of the probable message space.

How big is big enough? The DES (Data Encryption Standard) cryptosystem (which we will talk about shortly) has only 56-bit keys for a key space of size 2⁵⁶. A special DES Key Search Machine was built as a collaborative project by Cryptography Research, Advanced Wireless Technologies, and EFF. (See http://www.cryptography.com/resources/whitepapers/DES.html for details.) This machine was capable of searching 90 billion keys/second and discovered the RSA DES Challenge key on July 15, 1998, after searching for 56 hours. The entire project cost was under $250,000.

Today, 80-bit keys are probably still safe, but only barely so. 2⁸⁰ is only about 16 million times as large as the DES key space, and tens of thousand of machine on the Internet could conceivably be deployed in breaking a code. If not quite feasible using today’s PC’s (and I’m not saying it isn’t), it’s not that far-fetched to imagine searching an 80-bit key space in the foreseeable future. Much better are systems like triple DES (with 112-bit keys) and AES (with 128-bit keys), which will probably always be safe from brute-force attacks (but not necessarily from other kinds of attacks).