YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467b: Cryptography and Computer Security | Handout #3 | |
| Professor M. J. Fischer | January 20, 2010 | |
Random Number Generation
When writing programs, it is often necessary to generate random numbers in a given range or with a given distribution. The basic tool provided by Unix/Linux systems for generating a random number is the function rand(), which returns a uniformly distributed non-negative integer r with a value between 0 and RAND_MAX. Typically RAND_MAX == INT_MAX, the largest integer that can be represented by an int. In this document, we describe how to convert the value returned by rand() into a random value according to certain other useful distributions.
Suppose one wants to choose an integer k uniformly at random from the set {0,…,n - 1}. That is, each number should be chosen with probability exactly 1∕n.
A commonly-used method in C is to compute rand()%n. This produces a number in the desired range, but the probabilities aren’t quite correct. The reason is that if n does not exactly divide RAND_MAX, then some numbers are slightly more likely than others. To see this, suppose r is chosen uniformly from the set {0,…,RAND_MAX}, and suppose RAND_MAX = 8. Then r%3 = 0 when r is 0, 3, or 6, r%3 = 1 when r is 1, 4, or 7, and r%3 = 2 when r is 2 or 5. Thus 0 and 1 are each chosen with probability 3/8, but 2 is chosen with probabily only 2/8.
One way to fix this problem is to reject values of r that are 6 or 7 and to choose r again. Then the acceptable values of r are in the set {0,…,5}, and each occurs with probability 1/6.
In general, we’d like to use values of r that lie in the range {0,…,m - 1}, where m is the greatest multiple of n such that m - 1 ≤ RAND_MAX. We might be tempted to try to compute m = ((RAND_MAX + 1)∕n) * n. Unfortunately, this will lead to integer overflow problems since RAND_MAX+1 and possibly also m are too large to represent as int’s. Instead, we compute top = m- 1, the largest acceptable value of r, in a roundabout way:
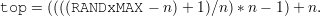
The order of evaluation is important to ensure that no intermediate result will overflow (assuming that n is reasonable), so we use parentheses to make the desired order of evaluation explicit.
Here is some code that should work:
Now we look at the problem of choosing a point x uniformly at random from the unit semi-open interval [0,1). Here, x will be of type double, so we need to convert the integer returned by rand() to a double and scale to the correct range. Again, the na´ve formula rand()/(RAND_MAX+1) fails because of integer overflow problems, but here the fix is simpler: just compute rand()/(RAND_MAX+1.0). The addition of the double constant 1.0 will cause RAND_MAX to be converted to a double before performing the addition, and the value RAND_MAX+1 is exactly representable as a double. Of course, this doesn’t really give the uniform distribution since most of the real numbers in [0,1) can never be chosen, but it is a good enough approximation for most applications.
Let U = {0,…,n- 1} and let P : U → [0,1] be a finite probability distribution, that is, ∑ k=0n-1P(k) = 1. We consider the problem of choosing an integer k from U according to the distribution P . Note that this is a generalization of the problem in section 2, but here we are willing to accept a small error in the derived probabilities.
The method here is to divide up the unit interval into n non-overlapping segments, where the length of segment j is P(j). Then we generate a random real x in the unit interval using the method of section 3, find the index k of the segment that contains x, and return k. We leave the coding of this method to the reader.