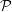 (n) be the multi-set that includes all prime factors of n. For example,
(n) be the multi-set that includes all prime factors of n. For example, 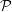 (8) = {2,2,2}
and
(8) = {2,2,2}
and 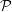 (12) = {2,2,3}.
(12) = {2,2,3}.
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467b: Cryptography and Computer Security | Handout #13 | |
| Xueyuan Su | April 4, 2010 | |
Solutions to Problem Set 4
Due on Wednesday, March 24, 2010.
In the problems below, “textbook” refers to Wade Trapp and Lawrence C. Washington, Introduction to Cryptography with Coding Theory, Second Edition, Prentice-Hall, 2006.
Textbook, exercise 3-7.
Solution: Let 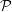 (n) be the multi-set that includes all prime factors of n. For example,
(n) be the multi-set that includes all prime factors of n. For example, 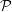 (8) = {2,2,2}
and
(8) = {2,2,2}
and 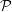 (12) = {2,2,3}.
(12) = {2,2,3}.

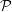 (a) or p
(a) or p 
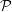 (b)
(or both). In the first case, p∣a and thus a ≡ 0 (mod p). In the second case, p∣b and thus
b ≡ 0 (mod p).
(b)
(or both). In the first case, p∣a and thus a ≡ 0 (mod p). In the second case, p∣b and thus
b ≡ 0 (mod p).
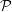 (n) ⊆
(n) ⊆ 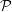 (ab). gcd(a,n) = 1 implies that
(ab). gcd(a,n) = 1 implies that 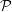 (n) ⁄⊂
(n) ⁄⊂ 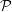 (a). Therefore, it
follows that
(a). Therefore, it
follows that  (n) ⊆
(n) ⊆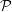 (b), and thus n∣b.
(b), and thus n∣b.Problem 2: Chinese Remainder theorem
Textbook, exercise 3-10.
Solution: Assume the smallest number is x. Then we set up the following formulas according to the available information.
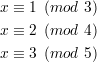
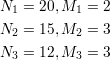
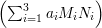 mod n = 58.
mod n = 58.
Let y be the next smallest number. We know that y = 58 + 60 = 118, because x ≡ y mod 60.
Textbook, exercise 3-12.
Solution: Because 101 is prime, we have ϕ(101) = 100. Since 2 is relatively prime to 101, 2  Z101*.
By Euler’s theorem,
Z101*.
By Euler’s theorem,
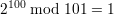
Let x be the remainder of dividing 210203 by 101. Then
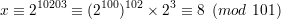
Thus, x = 8.
Textbook, exercise 3-20.
Solution:
 Zn*. By Euler’s theorem, aϕ(n) ≡ 1 (mod n). Thus
r ≤ ϕ(n), because r is the smallest positive integer such that ar ≡ 1 (mod n).
Zn*. By Euler’s theorem, aϕ(n) ≡ 1 (mod n). Thus
r ≤ ϕ(n), because r is the smallest positive integer such that ar ≡ 1 (mod n).
Textbook, exercise 3-27.
Solution:
 Zn* and thus x has 4 square roots module n. Thus, each
time the machine has a probability of 1∕4 returning the meaningful message m. The
expected number of trials is thus 4.
Zn* and thus x has 4 square roots module n. Thus, each
time the machine has a probability of 1∕4 returning the meaningful message m. The
expected number of trials is thus 4.
 Zn* and thus has 4 different square roots module n. Therefore, a + 1
and a - 1 are both non-zero. Since
Zn* and thus has 4 different square roots module n. Therefore, a + 1
and a - 1 are both non-zero. Since
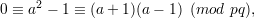
we have either p∣(a + 1) or q∣(a + 1). Without loss of generality, assume p∣(a + 1). Then Eve computes p = gcd(a + 1,n) and q = n∕p.
Problem 6: Adaptive chosen ciphertext attack against RSA
Textbook, exercise 6-7.
Solution: We know that 2 is relatively prime to n because n is a product of two odd primes. Therefore,
2  Zn*. By Euler’s theorem, 2ϕ(n) ≡ 1 (mod n). By the definition of RSA algorithm, ed ≡ 1
(mod ϕ(n)). Thus, we have
Zn*. By Euler’s theorem, 2ϕ(n) ≡ 1 (mod n). By the definition of RSA algorithm, ed ≡ 1
(mod ϕ(n)). Thus, we have
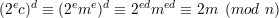
Let x = Dd(2ec mod n), where D is the decryption function used by Nelson. After obtaining x from Nelson, Eve computes the inverse of 2 module n by the extended Euclidean algorithm. Then Eve computes m = (2-1x) mod n.
Problem 7: Same modulus attack on RSA
Textbook, exercise 6-16.
Solution: Since eA and eB are relatively prime, gcd(eA,eB) = 1 and thus xeA + yeB = 1 for some integers x and y. Using extended Euclidean algorithm to solve this linear Diophantine equation, Eve gets a working pair (x,y). Then we have
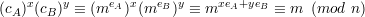
Thus, after intercepting cA and cB, Eve computes m = [(cA)x(cB)y] mod n.
Textbook, exercise 6-23.
Solution: Since gcd(e,12345) = 1, ex + 12345y = 1 for some integers x and y. Using extended Euclidean algorithm to solve this linear Diophantine equation, we get a working pair (x,y). Since m12345 ≡ 1 (mod n), we have
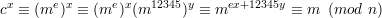
Thus, we decrypt m by computing cx mod n.