 Z*
761 that fails to be a primitive root of p, and use the Lucas test to prove your
answer correct.
Z*
761 that fails to be a primitive root of p, and use the Lucas test to prove your
answer correct.YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467b: Cryptography and Computer Security | Handout #8 | |
| Professor M. J. Fischer | March 19, 2012 | |
Problem Set 4
Due on Wednesday, March 28, 2012.
Work the problems below, prepare your answers in electronic form, and submit your solutions using the submit script on the Zoo. Remember to specify “3” for the problem number argument to submit.
Some of the problems require computation. You may use a calculator or computer for the calculations, but you must show your work. For example, in problem 1, your answer should contain a table of the relevant values of g(p-1)∕q mod p to demonstrate that the Lucas test gives the result you claim.
Some of the problems use terminology that we have not covered in class, even though we have talked about the concepts. You may use external resources to find out what these terms mean. As always, you must properly cite all resources that you use to solve the problems.
 Z*
761 that fails to be a primitive root of p, and use the Lucas test to prove your
answer correct.
Z*
761 that fails to be a primitive root of p, and use the Lucas test to prove your
answer correct.Problem 2: Security of Digital Signatures
Problem 3: Quadratic Residues and the Legendre Symbol
 {-1,1}, find a number xi,j
{-1,1}, find a number xi,j  Z*n
such that
Z*n
such that
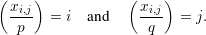
Let n = 703. Find a witness a for which the Miller-Rabin test succeeds in showing the compositness of n. Show the sequence of values b0,b1,b2,… that the test generates from a, and explain clearly why you can conclude from this sequence that n is not a prime.
Problem 5: Properties of Hash Functions
Hash functions are frequently used for cryptographic applications. A cryptographic hash function must have at least the properties listed below in order to withstand known attacks. For each of these properties, (1) say what it is, (2) give a plausible scenario whereby an attack exploiting a hash function lacking such property might be carried out, and (3) say whether there is an efficient hash function that has that property. (If yes, list that hash function; if no, explain why.)