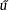Z and n
Z and n  Z+, there exist unique integers q,r such that a = nq + r and
0 ≤ r < n. We denote the quotient q by ⌊a∕n⌋ and the remainder r by a mod n. We say n
divides a (written n∣a) if a mod n = 0. If n∣a, n is called a divisor of a. If also 1 < n < |a|, n
is said to be a proper divisor of a.
Z+, there exist unique integers q,r such that a = nq + r and
0 ≤ r < n. We denote the quotient q by ⌊a∕n⌋ and the remainder r by a mod n. We say n
divides a (written n∣a) if a mod n = 0. If n∣a, n is called a divisor of a. If also 1 < n < |a|, n
is said to be a proper divisor of a.
 Z. For rapid convergence, take q = ⌊a∕b⌋, in which case
a - qb = a mod b.
Z. For rapid convergence, take q = ⌊a∕b⌋, in which case
a - qb = a mod b.
 Z and n
Z and n  Z+, we write a ≡ b (mod n) iff n∣(b-a). Note a ≡ b (mod n)
iff (a mod n) = (b mod n).
Z+, we write a ≡ b (mod n) iff n∣(b-a). Note a ≡ b (mod n)
iff (a mod n) = (b mod n).
 Z+. Let Zn = {0,1,…,n - 1} and let Z*n = {a
Z+. Let Zn = {0,1,…,n - 1} and let Z*n = {a  Zn∣gcd(a,n) =
1}. For integers a,b, define a ⊕ b = (a + b) mod n and a ⊗ b = ab mod n. ⊕ and ⊗
are associative and commutative, and ⊗ distributes over ⊕. Moreover, mod n distributes
over both + and ×, so for example, a + b × (c + d) mod n = (a mod n) + (b mod n) ×
((c mod n) + (d mod n)) = a⊕b⊗ (c⊕d). Zn is closed under ⊕ and ⊗, and Z*n is closed
under ⊗.
Zn∣gcd(a,n) =
1}. For integers a,b, define a ⊕ b = (a + b) mod n and a ⊗ b = ab mod n. ⊕ and ⊗
are associative and commutative, and ⊗ distributes over ⊕. Moreover, mod n distributes
over both + and ×, so for example, a + b × (c + d) mod n = (a mod n) + (b mod n) ×
((c mod n) + (d mod n)) = a⊕b⊗ (c⊕d). Zn is closed under ⊕ and ⊗, and Z*n is closed
under ⊗.
 Z, n
Z, n  Z+. Let d = gcd(a,n). If d∣b, then there are d solutions x
in Zn to the congruence equation ax ≡ b (mod n). If d ~ ∣ b, then ax ≡ b (mod n) has no
solution.
Z+. Let d = gcd(a,n). If d∣b, then there are d solutions x
in Zn to the congruence equation ax ≡ b (mod n). If d ~ ∣ b, then ax ≡ b (mod n) has no
solution.
 Z. For
rapid convergence, choose q = ⌊g∕g′⌋, and retain always last two triples. Note: Sequence of
generated g-values is exactly the same as the sequence of numbers generated by the Euclidean
algorithm.
Z. For
rapid convergence, choose q = ⌊g∕g′⌋, and retain always last two triples. Note: Sequence of
generated g-values is exactly the same as the sequence of numbers generated by the Euclidean
algorithm.
 Z+, a
Z+, a  Z. There exists unique b
Z. There exists unique b  Z such that ab ≡ 1 (mod n) iff
gcd(a,n) = 1. Such a b, when it exists, is called an inverse of a modulo n. We write a-1 for
the unique inverse of a modulo n that is also in Zn. Can find a-1 mod n efficiently by using
Extended Euclidean algorithm to solve ax ≡ 1 (mod n).
Z such that ab ≡ 1 (mod n) iff
gcd(a,n) = 1. Such a b, when it exists, is called an inverse of a modulo n. We write a-1 for
the unique inverse of a modulo n that is also in Zn. Can find a-1 mod n efficiently by using
Extended Euclidean algorithm to solve ax ≡ 1 (mod n).
 Z+, a
Z+, a  Z*n. Then aϕ(n) ≡ 1 (mod n). As a consequence, if r ≡ s
(mod ϕ(n)) then ar ≡ as (mod n).
Z*n. Then aϕ(n) ≡ 1 (mod n). As a consequence, if r ≡ s
(mod ϕ(n)) then ar ≡ as (mod n).
 Z+, a
Z+, a  Z*n. We define ord(a), the order of a modulo n, to be the
smallest number k ≥ 1 such that ak ≡ 1 (mod n). Fact: ord(a)∣ϕ(n).
Z*n. We define ord(a), the order of a modulo n, to be the
smallest number k ≥ 1 such that ak ≡ 1 (mod n). Fact: ord(a)∣ϕ(n).
 Z+, a
Z+, a  Z*n. a is a primitive root of n iff ord(a) = ϕ(n). For a primitive
root a, it follows that Z*n = {a mod n,a2 mod n,…,aϕ(n) mod n}. If n has a primitive
root, then it has ϕ(ϕ(n)) primitive roots. Primitive roots exist for every prime p (and for some
other numbers as well). a is a primitive root of p iff a(p-1)∕q ⁄≡ 1 (mod p) for every prime
divisor q of p - 1.
Z*n. a is a primitive root of n iff ord(a) = ϕ(n). For a primitive
root a, it follows that Z*n = {a mod n,a2 mod n,…,aϕ(n) mod n}. If n has a primitive
root, then it has ϕ(ϕ(n)) primitive roots. Primitive roots exist for every prime p (and for some
other numbers as well). a is a primitive root of p iff a(p-1)∕q ⁄≡ 1 (mod p) for every prime
divisor q of p - 1.
 Z*p such that b ≡ ak (mod p) for some
k, 0 ≤ k ≤ p - 2. We say k is the discrete logarithm of b to the base a.
Z*p such that b ≡ ak (mod p) for some
k, 0 ≤ k ≤ p - 2. We say k is the discrete logarithm of b to the base a.
 Zn such that x ≡ ai
(mod ni) for all 1 ≤ i ≤ k. To compute x, let Ni = n∕ni and compute Mi = Ni-1 mod ni,
1 <= i <= k. Then x = (∑
i=1kaiMiNi) mod n.
Zn such that x ≡ ai
(mod ni) for all 1 ≤ i ≤ k. To compute x, let Ni = n∕ni and compute Mi = Ni-1 mod ni,
1 <= i <= k. Then x = (∑
i=1kaiMiNi) mod n.
 Z, n
Z, n  Z+. a is a quadratic residue modulo n if there exists y such
that a ≡ y2 (mod n). a is sometimes called a square and y its square root.
Z+. a is a quadratic residue modulo n if there exists y such
that a ≡ y2 (mod n). a is sometimes called a square and y its square root.
 Z*p be a quadratic residue. Then a(p-1)∕2 ≡ (y2)(p-1)∕2 ≡ yp-1 ≡ 1 (mod p),
where y a square root of a modulo p. Let g be a primitive root modulo p. If a ≡ gk (mod p),
then a is a quadratic residue modulo p iff k is even, in which case its two square roots are
gk∕2 mod p and -gk∕2 mod p. If p ≡ 3 (mod 4) and a
Z*p be a quadratic residue. Then a(p-1)∕2 ≡ (y2)(p-1)∕2 ≡ yp-1 ≡ 1 (mod p),
where y a square root of a modulo p. Let g be a primitive root modulo p. If a ≡ gk (mod p),
then a is a quadratic residue modulo p iff k is even, in which case its two square roots are
gk∕2 mod p and -gk∕2 mod p. If p ≡ 3 (mod 4) and a  Z*p is a quadratic residue modulo
p, then a(p+1)∕4 is a square root of a, since (a(p+1)∕4)2 ≡ aa(p-1)∕2 ≡ a (mod p).
Z*p is a quadratic residue modulo
p, then a(p+1)∕4 is a square root of a, since (a(p+1)∕4)2 ≡ aa(p-1)∕2 ≡ a (mod p).
 Z*n is a quadratic residue modulo n
iff it is a quadratic residue modulo p and modulo q. The four square roots of a can be found
from its two square roots modulo p and its two square roots modulo q using the Chinese
remainder theorem.
Z*n is a quadratic residue modulo n
iff it is a quadratic residue modulo p and modulo q. The four square roots of a can be found
from its two square roots modulo p and its two square roots modulo q using the Chinese
remainder theorem.
 = 1 if a is a quadratic residue modulo p, -1
if a is a quadratic non-residue modulo p, and 0 if p∣a. Fact:
= 1 if a is a quadratic residue modulo p, -1
if a is a quadratic non-residue modulo p, and 0 if p∣a. Fact: 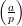 = a(p-1)∕2.
= a(p-1)∕2.
 = ∏
i=1k
= ∏
i=1k ei. (By convention, this product is 1 when k = 0, so
ei. (By convention, this product is 1 when k = 0, so 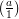 = 1.) The
Jacobi and Legendre symbols agree when n is an odd prime. If
= 1.) The
Jacobi and Legendre symbols agree when n is an odd prime. If  = -1 then a is definitely
not a quadratic residue modulo n, but if
= -1 then a is definitely
not a quadratic residue modulo n, but if  = 1, a might or might not be a quadratic residue.
= 1, a might or might not be a quadratic residue.
 can be computed efficiently by a straightforward recursive
algorithm, based on the following identities:
can be computed efficiently by a straightforward recursive
algorithm, based on the following identities: 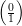 = 1;
= 1;  = 0 for n≠1;
= 0 for n≠1; 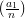 =
= 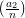 if a1 ≡ a2 (mod n);
if a1 ≡ a2 (mod n);  = 1 if n ≡ ±1 (mod 8);
= 1 if n ≡ ±1 (mod 8);  = -1 if n ≡ ±3 (mod 8);
= -1 if n ≡ ±3 (mod 8);
 =
= 
 ;
;  =
=  if a ≡ 1 (mod 4) or n ≡ 1 (mod 4);
if a ≡ 1 (mod 4) or n ≡ 1 (mod 4);  = -
= - if
a ≡ n ≡ 3 (mod 4).
if
a ≡ n ≡ 3 (mod 4).
 Z+. If n is composite, then for roughly 1/2 of
the numbers a
Z+. If n is composite, then for roughly 1/2 of
the numbers a  Z*n,
Z*n,  ⁄≡ a(n-1)∕2 (mod n). If n is prime, then for every a
⁄≡ a(n-1)∕2 (mod n). If n is prime, then for every a  Z*n,
Z*n,
 ≡ a(n-1)∕2 (mod n).
≡ a(n-1)∕2 (mod n).
 Z+ and write n-1 = 2km, where m is odd. Choose
1 ≤ a ≤ n - 1. Compute bi = am2i
mod n for i = 0,1,…,k - 1. If n is composite, then for
roughly 3∕4 of the possible values for a, b0≠1 and bi≠ - 1 for 0 ≤ i ≤ k - 1. If n is prime,
then for every a, either b0 = 1 or bi = -1 for some i, 0 ≤ i ≤ k - 1.
Z+ and write n-1 = 2km, where m is odd. Choose
1 ≤ a ≤ n - 1. Compute bi = am2i
mod n for i = 0,1,…,k - 1. If n is composite, then for
roughly 3∕4 of the possible values for a, b0≠1 and bi≠ - 1 for 0 ≤ i ≤ k - 1. If n is prime,
then for every a, either b0 = 1 or bi = -1 for some i, 0 ≤ i ≤ k - 1.