Instructions

Work the problems below, prepare your answers in electronic form, and submit your solutions using the submit script on the Zoo. Remember to specify “5” for the problem number argument to submit.

Some of the problems require computation. You may use a calculator or computer for the calculations, but you must show your work.

Some of the problems use terminology that we have not covered in class, even though we have talked about the concepts. You may use external resources to find out what these terms mean. As always, you must properly cite all resources that you use to solve the problems.

Problem 1: Quadratic Residues and the Legendre Symbol

1. Let p = 19, q = 37, and n = p×q = 703. For each i,j {-1,1}, find a number x_i,j Z* _n such that

2. Use the Euler criterion to justify your answers to part (a).

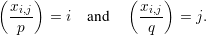
Problem 2: Properties of Hash Functions

Hash functions are frequently used for cryptographic applications. A cryptographic hash function must have at least the properties listed below in order to withstand known attacks. For each of these properties, (1) say what it is, (2) give a plausible scenario whereby an attack exploiting a hash function lacking such property might be carried out, and (3) say whether there is an efficient hash function that has that property. (If yes, list that hash function; if no, explain why.)

1. Preimage resistance
2. Second-preimage resistance
3. Collision resistance

Problem 3: ElGamal Authentication

Once Happy understood ElGamal signatures, he was excited to use them for authentication. He wants to send an authenticated message m to Bob so that Bob can verify that m came from him.

Here’s his idea. Assume that Happy has an ElGamal signing key (g,p,x) and Bob has the corresponding verification key (g,p,a). We denote the signing algorithm using that key pair by S and the verification algorithm by V .

	Happy		Bob
1.		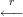	Choose random string r.
2.	Compute s = SA(r)		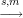Check V A(r,s).
			Accept m as coming from Happy if check succeeds.

1. Mallory wants to get Bob to accept a message m′ of his choosing. Describe in detail how he can do this using a man-in-the-middle attack.
2. Suggest a way to fix this protocol to thwart Happy’s attack. Your suggestion should not use any more rounds of communication nor assume any other encryption system or secret keys.
   [Hint: Think about using a secure hash function H to somehow “bind” m to the signature.]