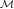 and ⊙
and ⊙ , where ⊙
, where ⊙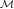 = ⊙
= ⊙ is:
is:
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467b: Cryptography and Computer Security | Handout #10 | |
| Professor M. J. Fischer | April 19, 2013 | |
Problem Set 7
Due on Wednesday, May 1, 2013.
Note that the due date falls on the last day of Reading Period. Late submissions can not be accepted without specific authorization from your Residential College Dean.
Instructions Work the problems below, prepare your answers in electronic form, and submit your solutions using the submit script on the Zoo. Remember to specify “7” for the problem number argument to submit. As always, you must properly cite all resources that you use to solve the problems.
Problem 1: Homomorphic Encryption
Consider the Caesar cipher extended to strings. Using the definition of homomorphic encryption given
in lecture 22, show whether or not the encryption function Ek is homomorphic with respect to operations
⊙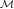 and ⊙
and ⊙ , where ⊙
, where ⊙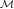 = ⊙
= ⊙ is:
is:
In each case, carefully define the message and ciphertext spaces that make sense for the operation, and give a
careful definition of the operation. Then argue why Ek is or is not homomorphic with respect to ⊙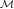 and
⊙
and
⊙ .
.
(over)
Problem 2: Anonymous Authentication
Consider the following proof of knowledge that allows Peggy to convince Victor that she knows either the discrete logarithm of y1 = gx1 or the discrete logarithm of y2 = gx2. Assume that Peggy knows x2. Peggy and Victor execute the following protocol.
| Peggy | Victor | ||
| 1. | Choose random v1,v2 and w | ||
| Compute t1 = y1wgv1, t2 = y2wgv2 | 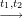 | ||
| 2. |  | Choose a random c | |
| 3. | Calculate c1 = w, c2 = c - c1, | ||
| r1 = v1 and r2 = v2 - x2c2 + x2c1 | 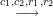 | Check t1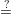 y1c1gr1, t2 y1c1gr1, t2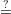 y2c2gr2, c1 + c2 y2c2gr2, c1 + c2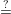 c c |
|
| Accept if checks succeed. | |||