Problem 0: Review old programming assignments, lectures, and readings. Use Piazza to suggest a question you feel is missing from this collection of practice problems.
Problem : Comment on the quality of the two suggested hash functions for arrays of integers, considering the conditions that are required for hash table operations to work in $O(1)$ expected time.
- the hash value is the bitwise exclusive-or of all the integers in the array
- the hash value is the sum of all the integers in the array
Problem : Consider the problem of, given a list of integers, checking whether they are all different. Give an algorithm for this problem with an average case of $O(n)$ under reasonable assumptions. Give an algorithm that has a worst case $O(n \log n)$.
Problem : Suppose we have the following hash function:
| s | hash(s) |
|---|---|
| ant | 43 |
| bat | 23 |
| cat | 64 |
| dog | 19 |
| eel | 26 |
| fly | 44 |
| gnu | 93 |
| yak | 86 |
Problem : Write pseudocode for a non-recursive version of an inorder traversal of a binary search tree. (Hint: for any node, where is the node with the next highest value?)
Problem : Draw the binary search tree that results from adding SEA, ARN, LOS, BOS, IAD, SIN, and CAI in that order. Find an order to add those that results in a tree of minimum height. Find an order to add those that results in a tree of maximum height. For your original tree, show the result of removing SEA, then show the order in which the nodes would be processed by an inorder traversal.
Problem : Repeat the original adds and delete from the previous problem for an AVL tree.
Problem : Repeat the original adds from the previous problem for a Red-Black tree.
Problem : Repeat the original adds and delete from the previous problem for a Splay tree using bottom-up splaying.
Problem :
Write pseudocode for the kdtree_for_each_range function.
This function has three parameters: a k-d tree,
a rectangular range specified by lower-left
and upper-right corners, and a function f
that takes a location as its
parameter and doesn't return anything.
The kdtree_for_each_range function passes each point in the
tree that is in the given range to the given function. The running time
should be $o(n) + k$ for a balanced tree, where $k$ is the number
of points in the range (so you should do something more efficient
than traversing the entire tree when $k$ is small).
Problem :
Consider the remove_incoming operation, which takes a
vertex $v$ in a directed graph and removes all incoming edges to that
vertex. Explain how to implement remove_incoming when the
graph is represented using an adjacency matrix and then for an adjacency list.
What is the asymptotic running time of your implementations in terms of
the number of vertices $n$ and the total number of edges $m$?
Problem : Show the result of running breadth-first search on the following directed graph. Start at vertex $a$ and after dequeueing a vertex, consider its neighbors in alphabetical order.
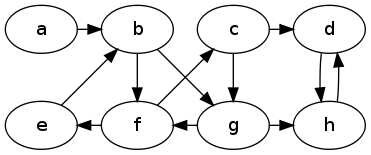
Problem : Show the result of running depth-first search on the graph in the previous problem. Start at vertex $a$ and when you get to a vertex, consider its neighbors in alphabetical order.