Objectives

• to use array-based lists
• to use dynamic memory allocation
• to resize arrays

Introduction

There are 52 cards in a standard French-suited deck. Each card consists of a rank (of which there are 13 in total) and a suit (of which there are 4 in total), as shown below.

An important aspect of most (if not all) of these games is randomization, or shuffling to increase the state space of the game and/or ensure that players don't know everything about other players' positions in the game. A good shuffle has two important properties: 1) the starting state has no bearing on the result of the shuffle, and 2) the shuffle produces all possible sequences of cards with equal probability. Consider a "perfect" shuffle, where a deck is split into two half-decks of equal size and cards are interleaved in a perfectly alternating fashion. An example is illustrated below with a toy deck consisting of eight cards.

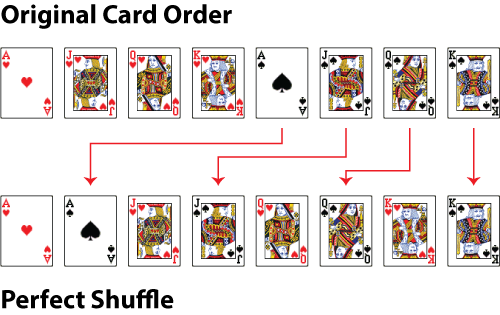
As one might expect, shuffling in this way isn't particularly good. The starting state does indeed influence the resulting state, and, for a 52 card deck, only a small number of possible sequences can result, even if the perfect shuffle is applied iteratively.

Now let's consider a popular shuffling technique, the "riffle." It's essentially a perfect shuffle, but, because it's performed by a human being, random imperfections in the shuffler's technique translate to randomness in the ordering of cards. This randomness is welcome given our two-fold goal, and, as it turns out, we can get a pretty good shuffle by applying the riffle technique six or seven times (depending on whom you ask).

But we can do better, significantly better. Enter the Fisher-Yates shuffle, an algorithm that can satisfy both of our goals in a single pass of the cards. As applied to our particular use case, it mandates that, for each card in the deck, we perform a swap with some randomly selected card that has not yet been swapped. Or, as a computer scientist might prefer to say, we iterate over each card c, and for c at index i we swap c with a randomly selected card whose index is between i and 51, inclusive.

Of course, we can claim that the shuffle is truly random if and only if we are able to select swap cards, well, randomly. Unfortunately for us, computers largely rely on pseudorandom number generators, or algorithms that generate sequences of numbers whose properties approximate the properties of sequences of random numbers. They are deterministic, and, in many cases, incapable of generating all possible sequences of cards (of which there are 52!, which is quite a large number). More on this problem later.

Assignment

Write a program called Deck that initializes a deck of playing cards, performs either some number of perfect shuffles or a Fisher-Yates shuffle, and prints each card of the deck to stdout. Each Card is a typedefed struct consisting of a rank and a suit. Output should be formatted as a sequence of ranks and suits delimited by singular spaces (e.g. AS KS TD ...). The mode under which the program operates is given by the flags -p or -fy for "perfect" and "Fisher-Yates," respectively. If both modes are specified, the program should print an error message to stdout and exit.

Under mode -p a single integer is given to specify the number of perfect shuffles performed. If a negative value is specified, an error is printed and the program exits. Under mode -fy a filename is provided, the contents of said file being integers (presumably selected randomly) representing swap indices for the shuffle. Consider the following example of a Fisher-Yates shuffle with an 4-card toy deck:

Deck: AC 2C 3C 4C

Swap indices: 2 2 1

Result after applying the first swap: 3C 2C AC 4C

Result after applying the second swap: 3C 4C AC 2C

Result after applying the final swap: 3C 4C 2C AC

As mentioned above, sometimes PRNGs aren't all that good, but a user may wish to nonetheless use one of these subpar PRNGs in Deck. Let's assume that the major deficiency of a given user's PRNG is that it cannot generate every sequence of cards with one simple pass. Similarly to how applying the riffle technique to a deck multiple times gives us a better shuffle, we can apply the Fisher-Yates shuffle with swap indices generated by the deficient PRNG to an arbitrary number of cards over an arbitrary number of iterations to give us a better shuffle.*

You can find template deck.h, deck.c, and deck_driver.c files with some basic functionality in /c/cs223/hw4/Optional/. Ultimately, your goal is to modify the provided code so as to be compatible with the function declarations given in /c/cs223/hw4/Required/deck.h.

To begin, notice that the function signatures given in /c/cs223/hw4/Required/deck.h differ drastically from those in the template files. More specifically, you'll find that only pointers to Decks are specified as return types. This convention is adopted because it enables the use of opaque structs. Under this paradigm, we can place the actual definition for the struct deck in deck.c and give a generic forward declaration in deck.h: typedef struct deck Deck;. Doing so encapsulates the struct away from outside programs, forcing them to interact with the functions defined for our Deck instead of directly manipulating its members. This behavior is desirable, as now we can modify the implementation for our abstract data type as we please without having to worry about breaking programs that rely on the details of its implementation. Getting back to the change in function signature, returns of type Deck * must be made instead of type Deck because our vague forward declaration doesn't tell the compiler anything about how big the struct actually is, and the compiler needs to allocate space for that return value. Because Deck * is a pointer, the compiler knows exactly how much space to allocate––it's the same as for all other pointers.

Also note that a Deck is defined as a statically allocated array of NCARDS cards. While, for this exercise, we won't need to grow the deck to some arbitrary size, we would nonetheless like to allocate cards on the heap to allow for games with larger decks like n-deck blackjack. For this reason, you'll want to change the mode of allocation for this array-based list from static to dynamic. In doing so, you'll need to change the implementation of deck_create to allocate space for the newly created deck and iteratively copy new cards into that space. In populating your new deck with cards, I'd recommend iterating over characters given in RANKS and SUITS. You'll also have to write a deck_destroy function to free the space allocated for the deck.

Additionally, consider that in deck_driver.c, the array swap_indices is statically allocated. Because our protocol is PRNG-agnostic, we'd like to leave it up to the user to indicate however many swap indices he or she feels will be necessary to make a Fisher-Yates shuffle truly random. So, it might be a good idea to dynamically allocate swap_indices and grow it as necessary, depending on the number of swap indices provided.

Finally, implement deck_fisher_yates_shuffle and deck_perfect_shuffle. Note that if the user provides a swap index that is out-of-bounds, Deck should interpret said index as either a 0 or 51 - i, where i gives the current index of the shuffle. Note that when reaching the 52nd, 104th, etc. swap index, the process restarts with card 0.

You should create a makefile with the executable Deck as the default target.

Submissions

[crb84@hawk hw4]$ /c/cs223/bin/submit 4 deck.c deck_driver.c makefile log
Copying deck.c
Copying deck_driver.c
Copying makefile
Copying log
[crb84@hawk hw4]$ /c/cs223/bin/testit 4 Deck
/home/classes/cs223/Hwk4/test.Deck
Copying deck.hExecuting /home/classes/cs223/Hwk4/test.Deck

Public test script for Deck (09/24/2020)

***** Checking for warning messages *****
Making -B ./Deck
gcc -g3 -Wall -std=c99 -pedantic   -c -o deck.o deck.c
gcc -g3 -Wall -std=c99 -pedantic   -c -o deck_driver.o deck_driver.c
gcc -g3 -Wall -std=c99 -pedantic -o Deck deck.o deck_driver.o

Each test is either passed or failed; there is no partial credit.

To execute the test labelled IJ, type one of the following commands
depending on whether the file /c/cs223/hw4/Tests/tIJ is executable or not
     /c/cs223/hw4/Tests/tIJ
     ./Deck < /c/cs223/hw4/Tests/tIJ
The answer expected is in /c/cs223/hw4/Tests/tIJ.out.


           Perfect Shuffling
PASSED  001. One shuffle
PASSED  002. Two shuffles
PASSED  003. Four shuffles
PASSED  004. 100 shuffles

           Perfect Shuffling: 4 points

           Fisher-Yates
PASSED  005. Swapping a few cards
PASSED  006. Swapping the first with the fifth
PASSED  007. Swapping the first with the last
PASSED  008. Performing more than 52 swaps
PASSED  009. Swapping nothing
PASSED  010. Running a few swaps under valgrind

           Fisher-Yates: 6 points

               Deductions for Violating Specification (0 => no violation)

End of Public Script

 10 points Total for Deck

           Possible Deductions (assessed later as appropriate)
               -10 Deficient style (comments, identifiers, formatting, ...)
                -5 Does not make
                -5 Makefile missing
                -5 Makefile incorrect
                -1 Log file incorrectly named
                -1 Log file lacks estimated time
                -1 Log file lacks total time
                -1 Log file lacks statement of major difficulties

***** Checking log file *****
Estimate: 2:00 ESTIMATE
Total: 2:00 TOTAL
  

*It should be noted, however, that the exact mechanisms by which shuffling is improved are very different.