Exercise 12: Heapsort
Objectives
- to implement a heap
- to implement an in-place $O(n \log n)$ sorting algorithm
Assignment
Code
Heap Functions (heapsort.c)
The heap_reheap_up function is intended to be used
when a new element $x$ is added at the last leaf or when an element $x$
is changed to a value larger than its previous value.
The function is passed the index where that new or modified element
$x$ is in the array.
In these situations, the array passed to heap_reheap_up
satisfies the max-heap property everywhere except possibly
between $x$ and the parent of $x$ (if there is one).
The function restores the max-heap order property by starting at
$x$ and, if $x$ is not the root and is larger
than its parent, swapping $x$ with its parent. The process
then continues at the location $x$ was swapped
into. The process stops when $x$ is not greater
than its parent or has been moved to the root.
Complete the heap_reheap_down function so that it
restores the max-heap order property in an array-based max-heap. At the
beginning of the function, the elements in the array will obey
the max-heap order except possibly at one element $x$ and any children
of $x$ – this would be the situation
after the value of $x$ was decreased or when the last element $x$
is moved to the root to fill the hole created when removing
the maximum element.
To restore the max-heap order property when it is violated,
heap_reheap_down should start at $x$
and swap $x$ with its largest child.
The process then continues at the location where $x$
was swapped to, stopping when
there is no longer a violation of the order property –
when $x$ has no children or is larger than all its children.
The heapsort function then uses heap_reheap_up
and heap_reheap_down to sort the array passed to it.
First, it repeatedly calls heap_reheap_up to add each
element to the array to create a heap.
Second, it repeatedly removes the largest
element from the heap, replaces that element with the element in the
last leaf, and calls heap_reheap_down to restore the
order property. The elements are then removed in reverse order and
are added back to the array starting at the end and going backwards
to put them in sorted order. Since there are $n-1$ calls to each of
heap_reheap_up and heap_reheap_down and
each call takes $O(\log n)$ time, the overall running time
of heapsort is $O(n \log n)$. (You can also use
heap_reheap_down working from the end of the array forward
in the first step, which reduces the time for the first step to
$O(n)$; since the second step still takes $O(n \log n)$ time, then
overall running time is still $O(n \log n)$, but with a smaller constant
hidden by the $O$.)
Unit Tests and TSP
Unit tests for the heap functions are implemented in
heap_unit.c.
Your makefile must include a target HeapUnit that is built
from the unit tests and your heapsort.c. The resulting
program will take a command-line argument to select the function
to test (-sort, -up, or -down,
an index into an array, and the elements to put in the array).
The elements in the array should be specified starting with the root
and going left to right within each successive level of the heap.
The index gives the location in the array of the only violation of
the max-heap order property.
There are two places in the implementation of the TSP program
that sort: the initialize_city_database function sorts the
array of cities and their locations by city code, and the
route_greedy sorts pairs of cities in order of increasing
distance. These two
functions have been modified to use heapsort instead
of merge_sort.
You will
need your implementation of union_find and
lugraph in order for the given
implementation of route_greedy in the TSP
executable to work, although you may
modify that implementation so that it does not use one or both
of those modules as long as you don't change the call to
heapsort that sorts the city pairs in order of increasing
distance.
Examples
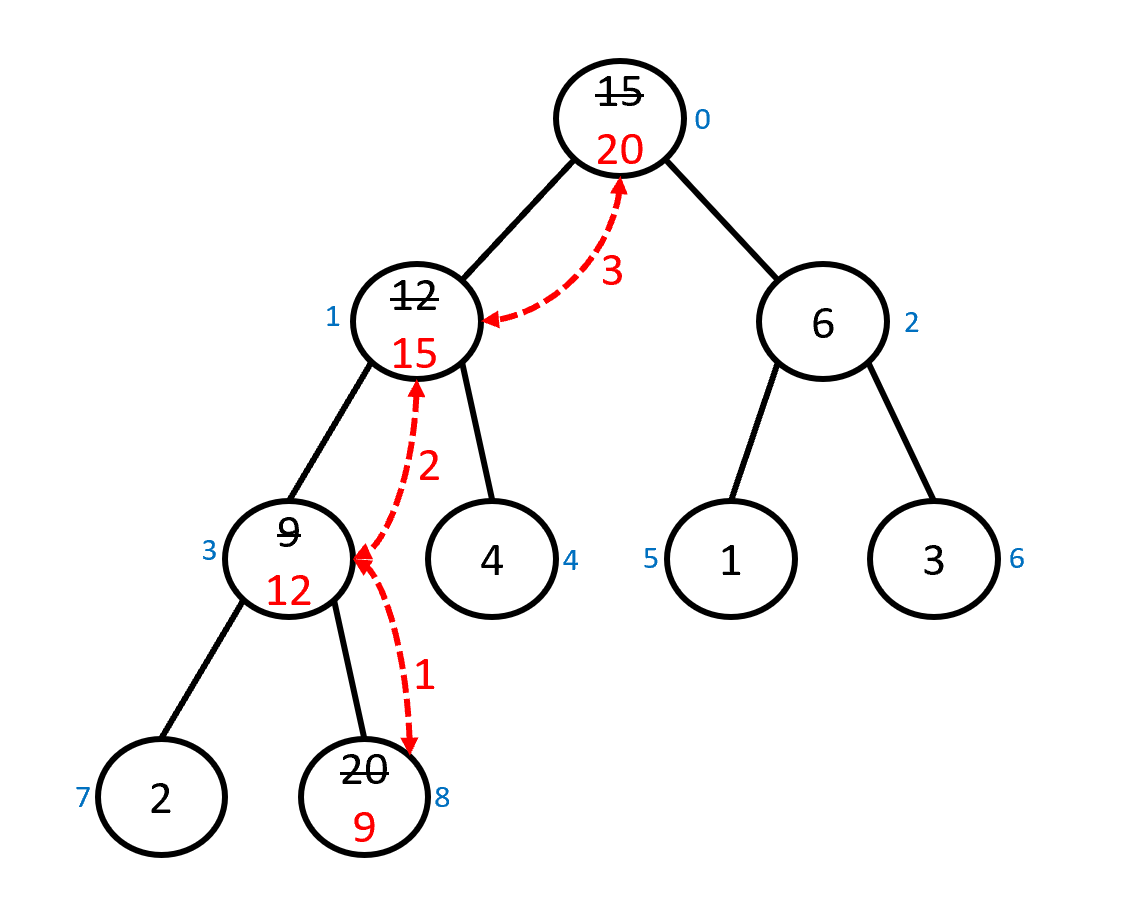
heap_reheap_up example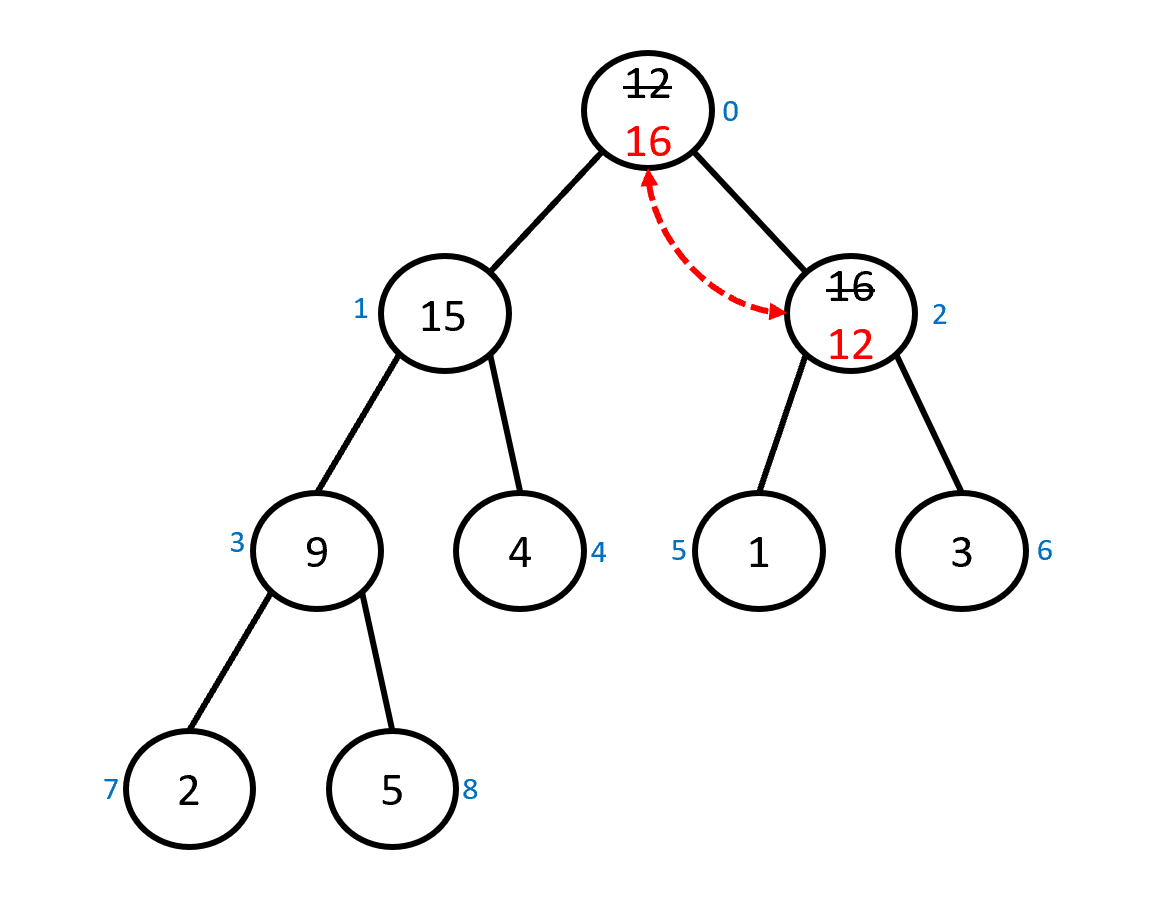
heap_reheap_down example
(base) [jrg94@cicada code]$ ./HeapUnit -up 8 15 12 6 9 4 1 3 2 20 PASSED (base) [jrg94@cicada code]$ ./HeapUnit -down 0 12 15 16 9 4 1 3 2 5 PASSED (base) [jrg94@cicada code]$ ./HeapUnit -sort X 3 9 1 15 6 12 5 2 4 PASSED (base) [jrg94@cicada code]$ ./TSP -greedy sea_6_dal.in -greedy: 9711.84 SEA IAH DAL MCI STL DCA BWI YVR SEA
Submissions
Submit as assignment 12 your modifiedheapsort.c,
your completed union_find.c from Exercise 6 (if necessary),
your completed lugraph.c from Exercise 11 (if necessary),
your tsp.c if you modified it,
any other files you created,
your makefile, and your log.
Your makefile should have the TSP executable as the default
target and HeapUnit as an additional target.
You need not submit the heapsort.h header
file, or any of the other supporting files
(and if you do, they will be ignored).