Project 4: Feedback Arc Set

Objectives

• to implement graph algorithms
• to choose data structures

Introduction

The feedback arc set problem is the problem of, given a directed graph, finding the smallest subset $S$ of the edges such that removing $S$ makes the graph acyclic. For example, the following graph has cycles UNC, FSU, Duke, UNC and UNC, Wake, FSU, Duke, UNC.

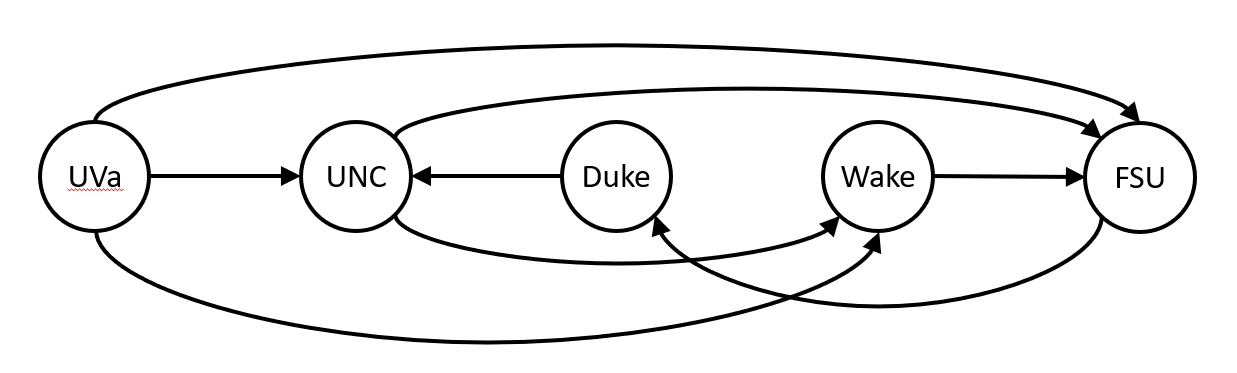
But removing the edges from UNC to FSU and from Wake to FSU breaks both of those cycles.

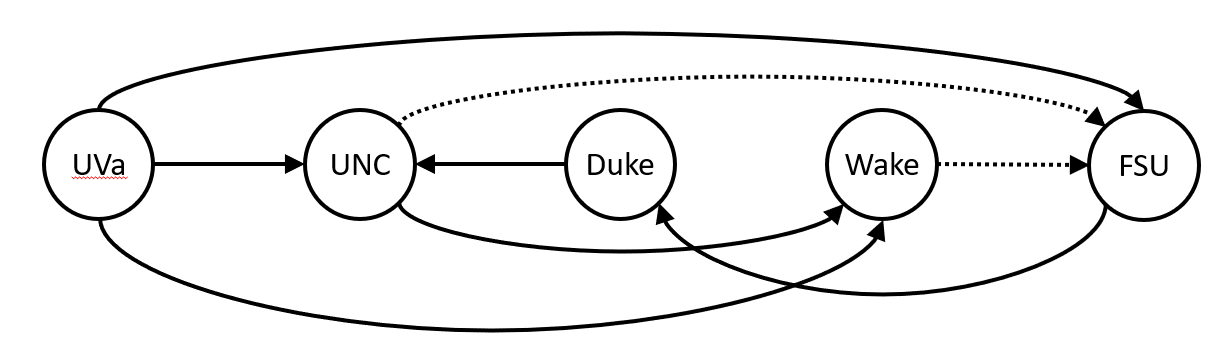
However, there is also a single edge that, when removed, leaves an acyclic graph.

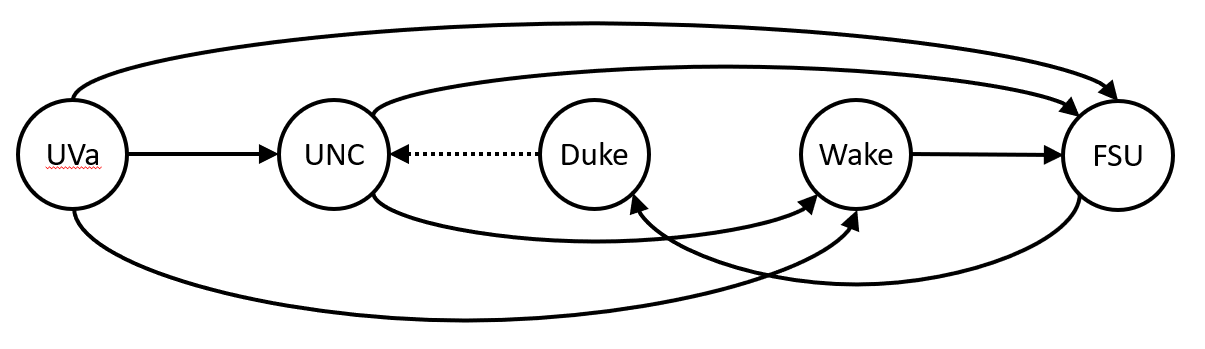
We can now move the vertices around so that all of the edges, except the edge from Duke to UNC, go left to right.

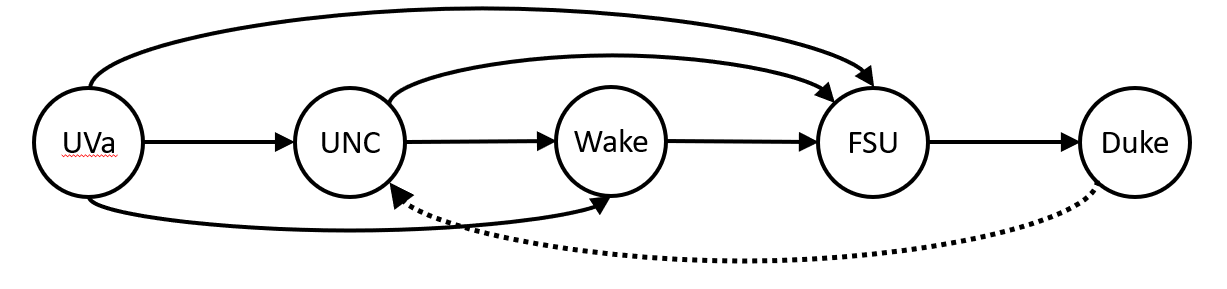
This illustrates that the feedback arc set problem is equivalent to the problem of ordering the vertices from left to right to minimize the number of edges that go right to left – removing those wrong-way edges would make the graph acyclic.

The graphs shown above reflect the results of a sequence of head-to-head matches between teams: the vertices represent teams and there is an edge from team A to team B if A beat B head-to-head. A minimum feedback arc set corresponds to a ranking that minimizes the number of upsets (results where a team listed earlier in the ranking lost to a team listed later).

In addition to sports, the feedback arc set problem has applications in many other areas, including graph visualization, clearing misinformation from social networks, and economics.

Like the travelling salesperson problem, the feedback arc set problem is NP-complete^* – if there were a polynomial-time algorithm for the feedback arc set problem, then there would also be a polynomial-time algorithm for the travelling salesperson problem and all other NP-complete problems. But no one has come up with a polynomial-time algorithm (the simple brute-force solution of checking every possible ordering of the vertices would have to check $n!$ orderings, which is not polynomial), and no one has been able to prove that no such algorithm exists.

We can, however, tell whether the graph is acyclic already (so no edges need to be removed) in $O(n + m)$ time using depth-first search – if we examine an edge and find that it goes to a vertex marked ACTIVE (one whose recursive call is still on the stack) then there is a cycle. If there are no cycles, then we can find an ordering that makes all the edges go from left to right (a topological sort).

If the graph has cycles, we can apply some heuristics in an attempt to find reasonably small sets of edges to remove. We will consider two heuristics: one based on the ratio of outdegree (the number of outgoing edges from a vertex) to total degree (the number of incoming + outgoing edges); and one based on depth-first search in which we traverse the outgoing edges of a vertex in order of decreasing outdegree of the destination, breaking ties in favor of lower indegree.

For example, for the first heuristic, we would order the vertices UVa (3/3), UNC (2/4), Duke (1/2), Wake (1/3), FSU (1/4).

For the second heuristic, we could start at UVa, visit UNC next since it has outdegree 2 and the other out-neighbors of UVa (Wake and FSU) have outdegree 1; then from UNC we can visit Wake (which has the same outdegree as FSU but lower indegree), then FSU, and finally Duke. The vertices in order of visitation are then UVa, UNC, Wake, FSU, Duke. We can repeat that process with every other possible starting point and choose the resulting ordering that minimizes the number of wrong-way edges.

(*) Formally, the related decision problems are NP-complete and the optimization problems we've been working on are NP-hard. The decision problem for feedback arc set is the problem of, given a directed graph and a nonnegative integer $k$, determining whether there is a subset of at most $k$ edges whose removal makes the graph acyclic. You will learn more about decision problems, NP-complete problems, and NP-hard problems in CPSC 365 or CPSC 366.

Assignment

Write a program called Rank that reads from standard input a list of game results and produces an ordering of the teams using either topological sort or one of the two heuristics for the feedback arc set problem. Which method to use will be specified by the first command-line argument: -topo for topological sort, -degree for the outdegree ratio heuristic, and -dfs for the DFS-based heuristic.

Standard input will contain the results of one game per line, with the winning team listed first and the losing team listed second. The winning team and losing team will be different (teams do not play themselves). Each team name will be enclosed in double quotes and may contain embedded whitespace (but not leading or trailing whitespace) and any other character aside from double quotes. Team names are case- and whitespace-sensitive (so "A Team", "A team", and "A  team" are all considered different). The two teams will be separated with a comma. There will be no whitespace aside from that between quotes and the newline at the end of each line. There may be multiple games between the same pair of teams, and in such cases there should only be one edge between the teams in the graph you apply the algorithms to; that edge should be from the team that won the most head-to-head games between the two, with no edge if each won the same number of games. For example, if the input is

"A","B"
"B","C"
"B","A"
"C","B"
"D","C"
"B","A"

then the resulting graph would have one edge from B to A and no edges between B and C (and an edge from D to C). Ties will be broken in some algorithms based on the order in which teams appeared in the input, and in such cases the first appearance on standard input counts even if the corresponding edge was cancelled out by a later game. In the above example, the order of appearance is A, B, C, D.

The output should be written to standard output and (except as noted) should consist of one line containing the number of wrong-way edges followed by one team name per line with the teams given in the order resulting from the selected algorithm. There should be nothing else written to standard output. If standard input was empty then the output should be empty as well.

For the -topo option, if the graph has cycles then there should be no output. If the graph is acyclic then there may be many possible topological sorts. The one output should be the one resulting from the following algorithm.

• Find all vertices with indegree 0 and output them in order of decreasing outdegree, with ties broken in favor of vertices that appear earlier in the input.
• Remove those vertices and all outgoing edges from those vertices.
• Find all vertices that have indegree 0 and output them in order of decreasing degree ratio in the original graph (outdegree divided by total degree), breaking ties in favor of higher outdegree and then in favor of vertices that appear earlier in the input.
• Remove those vertices and all outgoing edges from those vertices.
• Repeat the previous two steps until no vertices remain.

The -degree option should order the teams by decreasing degree ratio, listing vertices with degree 0 (neither incoming nor outgoing edges) last, and breaking ties as for the -topo option: in favor of vertices with higher outdegree and then in favor of vertices that appear earlier in the input.

The -dfs option should perform a depth first search starting with each vertex, and traversing edges in order of decreasing outdegree of the destination, breaking ties in favor of vertices with lower indegree and then in favor of vertices that appear earlier in the input. If there are unvisited vertices after running depth-first search from one starting point, then restart the search on the remaining unvisited vertices starting with the unvisited vertex with the highest outdegree, breaking ties as for selecting edges to traverse. Repeat that process until all vertices are visited before resetting the search for the next starting point. This will result in $n$ possible orderings – one for each possible starting point. The ordering that is output should be the one among those that minimizes the wrong-way (right-to-left) edges, breaking ties in favor of starting points that appear earlier in the input.

Running Time

• The -topo option must run in expected $O(k + n \log n)$ time, where $k$ is the number of lines of input.
• The -degree option must run in expected $O(k + n \log n)$ time, where $n$ is the number of distinct teams in the input.
• The -dfs option must run in expected $O(k + n^2 + nm \log m)$ time, where $m$ is the number of edges in the graph built from the input.

All running times are under the assumption that the length of the teams names is bounded, the team names are uniformly randomly distributed, and that malloc and free run in $O(1)$ time.

Error Handling

You may assume that the number of teams is small enough for a recursive implementation of depth-first search to work without running out of stack space. If any of the input (command-line arguments or standard input) is invalid for any other reason, then your program must behave gracefully (it must not crash or hang).

In all cases, your Rank program must execute with no valgrind errors.

ADTs

There is no starter code for this project. But you can and should make use of the implementations of ADTs used throughout the semester. You may modify them as necessary as long as you don't have any non-opaque structs that implement ADTs.

Example

(base) [jrg94@giraffe code]$ ./Rank -topo
"UVa","UNC"
"UVa","FSU"
"UVa","Wake"
"UNC","FSU"
"UNC","Wake"
"Duke","UNC"
"Wake","FSU"
"FSU","Duke"
(base) [jrg94@giraffe code]$ ./Rank -topo
"UVa","UNC"
"UVa","FSU"
"UVa","Wake"
"UNC","FSU"
"UNC","Wake"
"Wake","FSU"
"FSU","Duke"
0
UVa
UNC
Wake
FSU
Duke
(base) [jrg94@giraffe code]$ ./Rank -degree
"UVa","UNC"
"UVa","FSU"
"UVa","Wake"
"UNC","FSU"
"UNC","Wake"
"Duke","UNC"
"Wake","FSU"
"FSU","Duke"
2
UVa
UNC
Duke
Wake
FSU
(base) [jrg94@giraffe code]$ ./Rank -dfs
"UVa","UNC"
"UVa","FSU"
"UVa","Wake"
"UNC","FSU"
"UNC","Wake"
"Duke","UNC"
"Wake","FSU"
"FSU","Duke"
1
UVa
UNC
Wake
FSU
Duke

Submissions

Submit your makefile, your log file, and your source code necessary to build the Rank executable using your makefile as assignment 94. You must submit all code for any ADTs you use, even if you have not changed them from code provided for previous assignments. Your makefile should have the Rank executable as the default target.