Notes:

• For this class is is generally not necessary to validate input in your pseudocode: if a problem says the input will be in a certain form then write your pseudocode under the assumption that the input is in that form.
• "Find/devise/give an efficient algorithm" means "find an algorithm that is as efficient as possible, and you have to figure out for yourself whether your solution can be improved."

Problem : Devise an efficient algorithm that, given an sequence of integers $a_1, a_2, \ldots, a_n$, the length of the sequence ($n$), and a nonnegative $k$, determines if there is a run of at least $k$ consecutive equal values in the sequence. For example, if the sequence is $1, 3, 3, 1, 1, 2, 2, 2, 37$ and $k = 3$ then the result should be true because there are 3 2's in a row, but if $k = 4$ then the result should be false. Use an invariant to prove that your algorithm is correct.

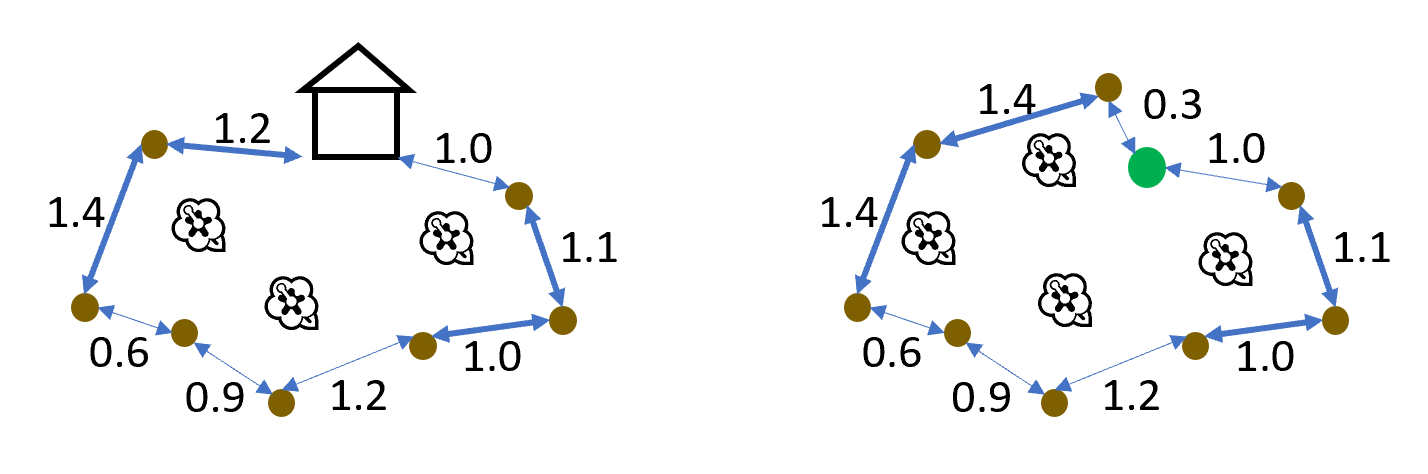
Problem :

• Prof. and Mrs. Glenn need to build a fence around their yard to keep the deer from eating their azaleas. The fence will start at one corner of their house and end at another. The perimeter of their yard is marked by trees, and the fence must follow that perimeter. Furthermore, the fencing is sold in lengths of $L$ and, to avoid setting fenceposts, each segment of fencing must start and end at either a corner of the house or a tree; the next segment then starts at the tree where the previous segment ended. Segments less than $L$ are possible, but the scraps may not be reused in other parts of the fence.

  Devise a $\Theta(n)$ algorithm to determine the minimum number of fencing segments the Glenns must buy to complete their fence, and prove that your algorithm is correct. The inputs should be as follows: 1) $d$, a non-empty list of the distances along the perimeter of the yard to each tree in increasing order, starting with 0.0 for the first corner of the house, with no two consecutive elements more than $L$ apart, and ending with the total length of the perimeter; 2) $L$, the length of the segments of fencing; and 3) $n$, the number of trees along the perimeter (so the number of elements in $d$ is $n + 2$). The output should be the ordered list of $k+1$ segment endpoints, where $k$ is the number of segments used. You may use a simple sequential search as part of your algorithm without proving that the sequential search is correct (although that is a good exercise).

• Consider the above problem, except: 1) there is no house where the fence must start and end, so the fence may start at any tree and must go all the way around the perimeter and end at the starting tree; 2) there is an additional input $q$ giving the minimum number of trees within any length of $L$ around the perimeter that starts at a tree; and 3) the index $k$ in list $d$ of a tree that is at the beginning of a length of $L$ that contains $q$ trees (that interval possibly wraps around back to tree 0 and beyond).

  Find an efficient algorithm to find the minimum number of segments of fence required (the input and output are as before, but $d$ ends with $P$, the total length of the perimeter, and the output should end with $s+P$, where $s$ is the value it starts with). Explain what the worst-case running time of your algorithm is. You need not prove that your algorithm is correct.

Problem : Consider the problem of scheduling overnight stops for a hiker on a long-distance trek. Each overnight stop must be in a cabin; the distances from the start of the trek to each cabin is given in an array called loc (so the difference between two elements in the array gives the distance between the corresponding cabins). The hiker can travel up to max_d units each day. And with some extra effort, the hiker can travel a little more. But the extra effort takes a toll on the hiker: the total extra effort over the entire trek must not exceed max_e; resting by travelling less than max_d does not affect this.

For example, if the locations of the cabins are [0.0, 1.0, 1.1, 2.0, 2.2, 3.0, 3.5] with max_d = 1.0 and max_e=0.5, then the hiker can complete the trek in 3 days by expending 0.1 extra effort to reach the cabin at 1.1 on the first day, expending another 0.1 extra effort to reach the cabin at 2.2 on the second day, and then expending the remaining 0.3 extra effort to get to the destination, exhausted, on the third day.

The following algorithm schedules the hiker's stops greedily by finding the furthest cabin the hiker can travel to on each day by possibly expending all the remaining extra effort.

Prove that this algorithm returns a shortest possible list of stopping points, or find an example of input parameters that are consistent with the preconditions for which the output is not optimal, explaining what the output is for those inputs and what an optimal schedule is.

FUNCTION schedule_travel(loc, max_d, max_e)
# Preconditions:  
# loc is the list of distances from the starting point of each potential
# stopping points; the first element will be 0.0 (for the distance from
# the starting point to itself), and no two consecutive elements will have
# a difference of more than max_d
#
# max_d is a positive number giving the maximum distance that can be
# travelled in a day without extra effort
#
# max_e is a nonnegative number giving the maximum allowed sum of extra effort

# start at beginning
start <- 0                    # start at beginning
stop_points <- []             # list of stopping points is initially empty
remaining_extra <- max_e      # have all our extra effort left to use
	 
# loop until starting point for current day is the destination
while start < len(loc) - 1:
    stop <- start + 1         # first potential stop to try is one just after start

    # advance stopping point for current day until at destination or the
    # next stopping point is invalid, even with extra effort	       
    while stop < len(loc) - 1 and loc[stop + 1] - loc[start] <= max_d + remaining_extra:
        stop <- stop + 1

    # account for extra effort if travelled more than max_d on current day
    if loc[stop] - loc[start] > max_d:
        remaining_extra <- remaining_extra - (loc[stop] - loc[start] - max_d)

    start <- stop             # starting point for next day is stoping point for current day 
    stop_points.append(stop)  # add stop to end of list of stopping points

return stop_points

Problem :

• Consider the following job scheduling problem. We are given all at once $n$ jobs with positive lengths $t_1, t_2, \ldots, t_n$. We can schedule only one job at a time and once we start a job we must run it to completion. A schedule for a set of jobs is then the starting time for each job $s_1, s_2, \ldots, s_n$. Find an efficient algorithm to schedule the jobs to minimize the total wait time, where the wait time for a job is the difference between the time the job arrived and when it finished. Since all jobs arrive at the same time $t=0$, the wait time for job $i$ simplifies to $s_i + t_i$ and so the problem is to schedule the jobs to minimize $\sum_{i=1}^n(s_i + t_i)$. Prove that your algorithm is correct.
• Consider the above problem, but associate with the jobs positive values of importance $w_1, \ldots, w_n$, and minimize $\sum_{i=1}^n w_i(s_i + t_i)$. Find an efficient algorithm to determine an optimal schedule in this case. You need not prove that your algorithm is correct.