Notes:

• For this class is is generally not necessary to validate input in your pseudocode: if a problem says the input will be in a certain form then write your pseudocode under the assumption that the input is in that form.
• "Find/devise/give an efficient algorithm" means "find an algorithm that is as efficient as possible, and you have to figure out for yourself whether your solution can be improved."

Problem : Prove or disprove: for any connected graph $G$ with vertex set $V$ and edge set $E$ and non-negative, not necessarily distinct weights on the edges, for all minimum spanning trees $T$ of $G$, each edge $(v, w)$ in $T$ is a minimum-weight edge across some cut that some subset of $T$ respects.

Problem : Consider the following algorithm for computing a minimum spanning tree in a connected graph $G$ with vertex set $V = \{0, 1, \ldots, n-1\}$ and edge set $E$, in which the edges have distinct non-negative weights.

• $A \leftarrow \emptyset$
• while the graph $(V, A)$ has more than one connected component
  • $L \leftarrow \emptyset$
  • for each connected component $C$ in $(V, A)$
    • find the minimum-weight edge $(u, v)$ where $u \in C$ and $v \not\in C$
    • $L \leftarrow L \cup \{(u, v)\}$
  • for each $(u, v) \in L$,
    • $A \leftarrow A \cup \{(u, v)\}$

• Show how to implement this algorithm in worst-case $O(m \log n)$ time and explain why your implementation runs in $O(m \log n)$ time. (This will involve choosing data structures, including for $V$ and $E$, and reasoning about the number of iterations of the loop. You need not prove that your particular implementation is correct. You may optimize the pseudocode somewhat; the test for whether you are implementing the given algorithm faithfully is whether the sequence of values of $A$ at the beginning of the outer loop is the same as what would be given by the pseudocode.)

Problem : Imagine a transportation network in which cities are linked by two modes of transportation: fast but expensive Hyperloop tubes and slow but cheap on-demand self-driving cars. Two cities may or may not be linked directly (without requiring a transfer in another city), but if they are linked by one mode they are linked by the other as well. For any pair of linked cities, the travel time is known and consistent (no congested traffic!) for both modes of transportation, and the Hyperloop is always at least as fast as the self-driving cars (and neither mode can send you back in time). Wait times and transfer times are negligible.

Suppose you have plenty of money for self-driving cars but can't afford any Hyperloop trips – except you have a one-time promotional code good for free travel between any pair of cities linked directly to each other. You need to find the fastest way to travel from your home city to some other given city (Baltimore, for example, has a great aquarium, baseball stadium, free art museums, restaurants...). Model this problem as a graph problem, describe an efficient algorithm to solve it, and prove that your algorithm is correct (hint: if you use an existing algorithm then you don't have to repeat the proof that it is correct, but you do have to explain how your use of it results in the correct output).

Problem : Consider an undirected graph with non-negative weights on the edges and with a special property: it can be broken down into a 2-D grid of cells with $k$ cells total where each cell has 4 special "corner" vertices shared with its neighbors plus $k$ other "interior" vertices, the degree of all vertices is bounded by a constant $c$, and none of the edges go between interior vertices in different cells or between non-adjacent grid corners.

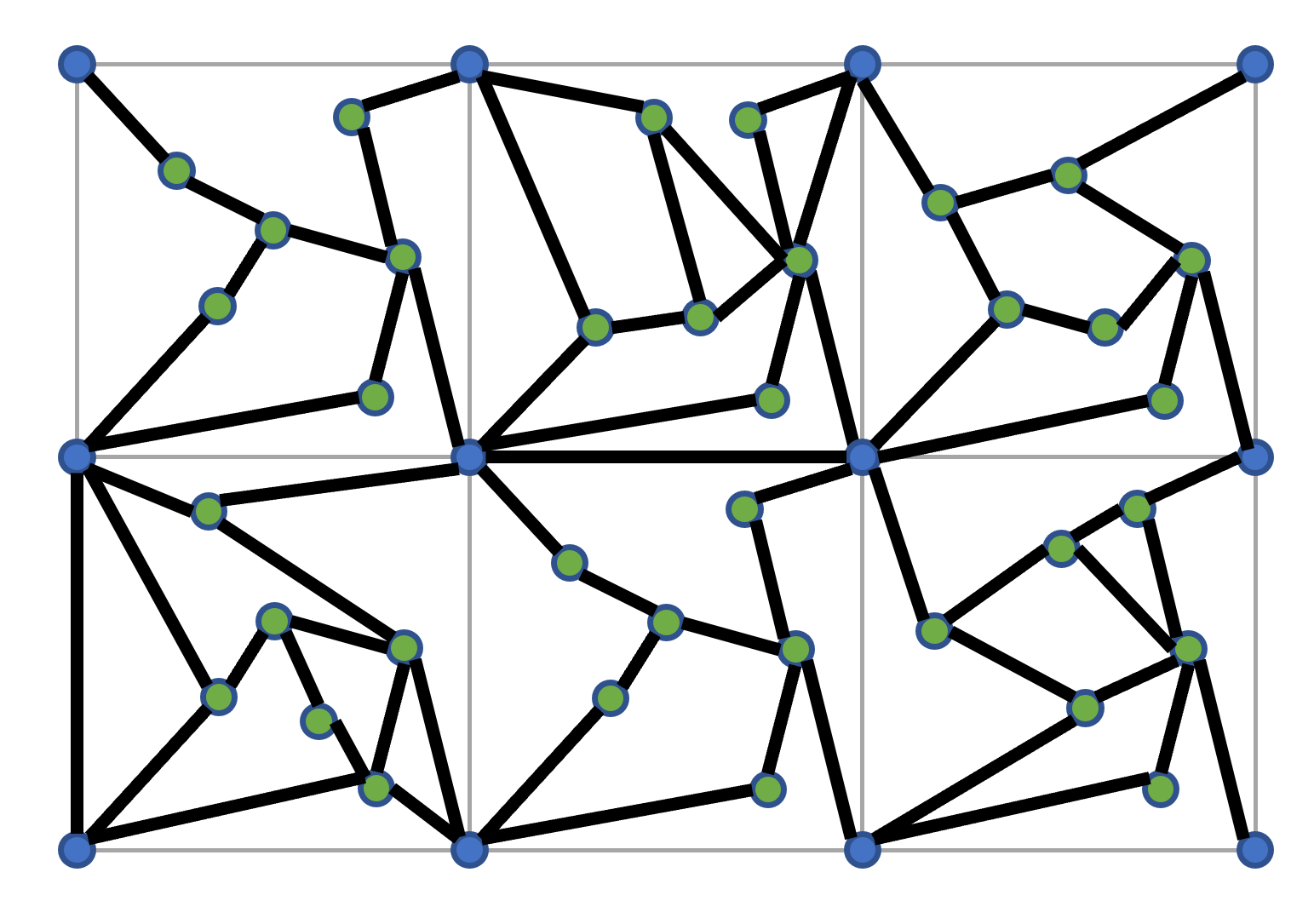
Devise a worst-case $O(k^2 \log k)$ algorithm that, given the graph represented using adjacency lists, the width and height of the grid, and a list of $k$ pairs of vertices in the graph, outputs for each pair the total weight of the minimum-weight path between the pair. Explain why your algorithm meets the time bound. You may assume that each corner vertex is labelled with $(r, c)$ giving its position in the grid (with $(0, 0)$ being the upper left corner of the upper left cell), and each interior vertex is labelled with $(r, c, i)$ giving which grid cell it is in and its 0-based index within that cell (with cell $(0, 0)$ being the upper left cell, so that cells are labelled the same as their upper left corners), and that you can distinguish between the two different label types and extract their components in constant time.