Notes:

• For this class is is generally not necessary to validate input in your pseudocode: if a problem says the input will be in a certain form then write your pseudocode under the assumption that the input is in that form.
• "Find/devise/give an efficient algorithm" means "find an algorithm that is as efficient as possible, and you have to figure out for yourself whether your solution can be improved."

---

Problem : The following function finds, for each element of a sorted array, the the largest element that is within a certain distance beyond it.

More formally, it takes as input

• $A$, a nonempty array of real numbers in strictly increasing order (indexed starting from 0),
• $n$, the size of the array A, and
• $L$, a positive number,

and returns an array $B$ of length $n$ so that, for $0 \le i \lt n$, $$B[i] = \max_{\substack{0 \le k \lt n \\ A[k] \le A[i] + L}} A[k]$$.

For example, if $A = [1.0, 1.5, 2.1, 2.6, 2.9, 3.0, 4.2, 5.0, 5.2, 6.3, 7.0, 8.0, 8.5, 9.1, 9.6, 9.9, 10.0]$ (so $n=17$) and $L = 3$, then the returned array would be $B = [3.0, 4.2, 5.0, 5.2, 5.2, 5.2, 7.0, 8.0, 8.0, 9.1,10.0,10.0,10.0,10.0,10.0,10.0,10.0]$.

def farthest_reachable(A, n, L):
    Q = a new deque containing only A[0]
    B = an empty list
    i = 1
    while i < n or length(Q) > 0:
        if i < n and (size(Q) == 0 or A[i] <= peek_front(Q) + L):
            append(Q, A[i])
            i = i + 1
        else:
            append(B, peek_back(Q))
            delete_front(Q)
    return an array containing the elements of B

Write the loop invariant for the loop inside this function. Your invariant should be complete, so that we could prove that the function is correct using your invariant, but you needn't actually complete the proof yourself. (Pedants: you may omit "$A$ (and $n$ and $L$) contain their original values" since there are no assignments that modify those parameters. You may omit "$i$ is an integer" [but not other conditions on $i$, no matter how trivial] since the only arithmetic used in an assignment to $i$ is addition of integers, which will always yield an integer. You may omit similar claims in future problems.)

There is a Python implementation available that can be run on the Zoo with python3 /home/httpd/html/zoo/classes/cs365/s2020/Homework/farthest_reachable.py to help you see the relationships between i, B, and Q as the algorithm progresses.

---

Problem : The following function finds the element in a sorted array that has the fewest elements within a certain distance after it.

More formally, it takes as input

• $A$, a nonempty array of real numbers in strictly increasing order (indexed starting from 0),
• $n$, the size of the array $A$,
• $L$, a positive number less than or equal to $A[n - 1] - A[0]$, and
• $m$, the largest integer such that $0 \le m \lt n$ and $A[m] + L \le A[n-1]$ (note that $m$ is determined by the other inputs but we are assuming it is given instead of computing it ourselves, and $m$ exists because the precondition on $L$ means that $A[0] + L \le A[n-1]$), so there is at least one integer thast satisfies the condition)

and returns the index $k$ into $A$ such that $0 \le k \le m$ and size of the set $\{A[i] \mid A[k] \lt A[i] \le A[k] + L\}$ is minimized, breaking ties in favor of smaller $k$s

For example, if $A = [1.0, 1.5, 2.1, 2.6, 2.9, 3.0, 4.2, 5.0, 5.2, 6.3, 7.0, 8.0, 8.5, 9.1, 9.6, 9.9, 10.0, 11.2]$ and $L = 3$, then $n = 18$, $m = 11$, and the returned index would be 5 because the elements in $A$ within $3$ after $A[5]$ are $\{4.2, 5.0, 5.2\}$ and that is the smallest possible.

def fewest_within(A, n, L, m):
    i = 0
    j = 0
    c = 0
    min_span = n
    k = None
    while i <= m:
        if j + 1 < n and A[j + 1] <= A[i] + L:
            # advance j as far as it can go for the current i
            j = j + 1
        else:
            # j is now as far as it can go;
            # j - i is the number of elements with L after A[i]
            span = j - i
            if span < min_span:
                min_span = span
                k = i
            i = i + 1
        c = c + 1
    return k

Prove that the function is correct with respect to its preconditions and postconditions using the following loop invariant. You only need to prove that the first, fourth, and fifth parts are maintained by the loop body (but complete all of the basis, termination, and postcondition parts of the proof).

• $i + j = c$
• $i \le m + 1$
• $0 \le j \le c, n - 1$
• $A[j] \le A[i] + L$
• $k$ is the index of the element in the first $i$ places in $A$ that minimizes the number of elements within $L$ after it, with ties broken in favor of lower indices, or both $k$ is None and $i = 0$
• if $k$ is not None then $min\_span$ is the number of elements after $A[k]$ within $L$ of it; otherwise $min\_span = n$

(We take as given that the inputs aren't changed and that $c$ counts the number of iterations of the loop.)

---

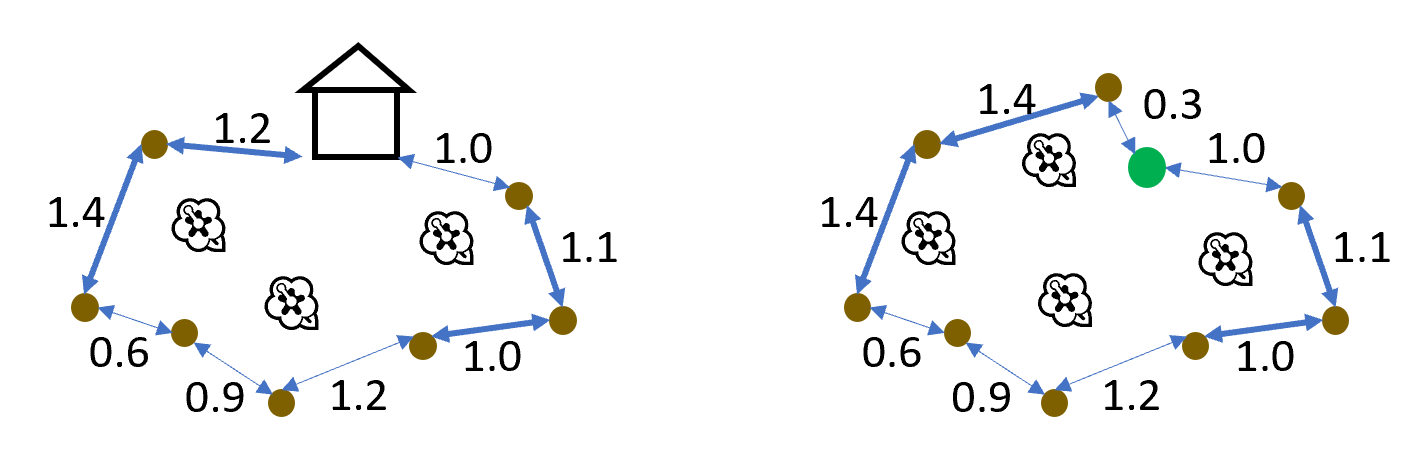
Problem : Prof. and Mrs. Glenn need to build a fence around their yard to keep the deer from eating their azaleas. The fence will start at one corner of their house and end at another. The perimeter of their yard is marked by trees, and the fence must follow that perimeter. Furthermore, the fencing is sold in lengths of $L$ and, to avoid setting fenceposts, each segment of fencing must start and end at either a corner of the house or a tree; the next segment then starts at the tree where the previous segment ended. Segments less than $L$ are possible, but the scraps may not be reused in other parts of the fence.

Devise a $\Theta(n)$ algorithm to determine the minimum number of fencing segments the Glenns must buy to complete their fence, and prove that your algorithm is correct. The inputs should be as follows:

• $d$, a non-empty list of the distances along the perimeter of the yard to each tree in increasing order, starting with 0.0 for the first corner of the house, with no two consecutive elements more than $L$ apart, and ending with the total length of the perimeter;
• $L$, the length of the segments of fencing; and
• $n$, the number of trees along the perimeter (so the number of elements in $d$ is $n + 2$).

The output should be the ordered list of $k+1$ segment endpoints, where $k$ is the number of segments used. You may use a simple sequential search as part of your algorithm without proving that the sequential search is correct (although that is a good exercise).

---

Problem : Consider the previous problem, with the following modification: there is no house where the fence must start and end, so the fence may start at any tree and must go all the way around the perimeter and end at the starting tree.

Find an efficient algorithm to find the minimum number of segments of fence required (the input and output are as before, but $d$ ends with $P$, the total length of the perimeter, and the output should end with $s+P$, where $s$ is the value it starts with). Explain what the worst-case running time of your algorithm is. You need not prove that your algorithm is correct.