Notes:
- For this class is is generally not necessary to validate input in your pseudocode: if a problem says the input will be in a certain form then write your pseudocode under the assumption that the input is in that form.
- "Find/devise/give an efficient algorithm" means "find an algorithm that is as efficient as possible, and you have to figure out for yourself whether your solution can be improved."
Problem : Consider the clean bicycle routing problem: finding a route from a starting point to a destination that minimizes total distance over dirt roads, breaking ties by total distance. For example, a route of 50 total miles with no dirt roads would be favored over a 2 mile route with 1 mile on dirt roads.
Formally, the problem is: given a starting vertex and a destination vertex in a directed graph in which each edge is labelled with the total distance and the distance on dirt roads (where $d_{tot} \ge d_{dirt} \ge 0$ for each edge), find a "best" route from the start to the destination, where path $P$ is better than path $P'$ if either
- $P$ has a lower sum of dirt road distance over all its edges than $P'$, or
- the dirt road distances are the same and $P$ has a lower sum of total distances than $P'$.
- Prove that if $P$ is a best route from $u$ to $v$ and a best route $P'$ from $x$ to $y$ goes through $u$ and then $v$ (so $P'$ can be split into three parts: $P_1$ from $x$ to $u$, $P_2$ from $u$ to $v$, and $P_3$ from $v$ to $y$), then $P_1PP_3$ is also a best route from $x$ to $y$.
- Give an efficient algorithm for finding best routes. The input is an adjacency list representation of the graph with the total and dirt distances of each edge recorded in the adjacency list elements, the starting point $u$, and destination $v$. Compute the asymptotic running time of your algorithm, explaining your computation. Include in your explanation what choices you've made for representing other ADTs used in your solution. You need not prove that your algorithm is correct.
Problem : Devise an efficient algorithm for determining the location of food deserts. The input is
- an undirected, connected, weighted graph $G$ with vertices $1, \ldots, n$; this graph represents a sparse street network ($m \in \Theta(n)$), where the vertices are intersections and the weights are distances between the intersections;
- an array $pop$ where $pop[i]$ gives the population at each intersection (for simplicity we imagine people living at the intersections instead of along the edges);
- a non-empty list $S$ of the intersections where a sufficient variety of nutritious foods can be purchased, and $k$, the length of that list (there may be non-zero population at those intersections too);
- $b$, which defines our notion of what a food desert is: for each intersection we find the shortest path to any intersection in $S$. Any intersection that is strictly farther away from all intersections in $S$ than the $b$ closest people are considered to be in a food desert.
The output should be a list of the intersections that are food deserts. Compute the asymptotic running time of your algorithm, explaining your computation. Include in your explanation your choice of representation for the graph and other ADTs used in your solution. You need not prove that your algorithm is correct.
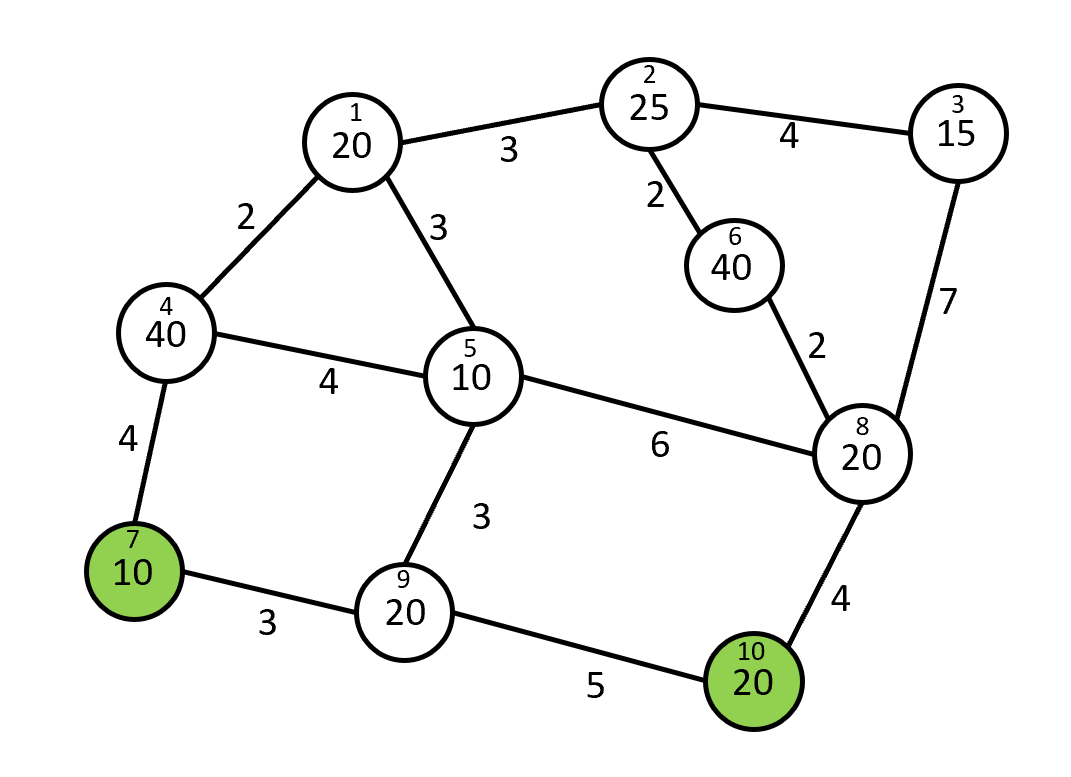
| Vertex | Closest Food | Dist. | Pop. | Cumulative Pop. |
|---|---|---|---|---|
| 7 | 7 | 0 | 10 | 10 |
| 10 | 10 | 0 | 20 | 30 |
| 9 | 7 | 3 | 20 | 50 |
| 4 | 7 | 4 | 40 | 90 |
| 8 | 10 | 4 | 20 | 110 |
| 5 | 7 | 6 | 10 | 120 |
| 1 | 7 | 6 | 20 | 140 |
| 6 | 10 | 6 | 40 | 180 |
| 2 | 10 | 8 | 25 | 205 |
| 3 | 10 | 11 | 15 | 220 |
The small number in each vertex is its index; the large number is its population. The table shows vertices sorted by distance to closest food source, with cumulative population. $S$ is $[7, 10]$. When $b = 130$, the output would be $[2, 3]$ or $[3, 2]$ since the closest 130 people live within 6 or closer of an intersection in $S$ and the people who live at $2$ and $3$ are strictly farther than that (8 and 11 respectively). Note that the people at vertex 6 are at the same distance as those at vertices 1 and 5, so they are not in a food desert – the "strictly farther" condition disambiguates cases like this where reordering vertices that are all at the threshold distance (5, 1, and 6 in this example) would result in different sets containing the closest $b$.
Problem : Prove that if there is no unique minimum spanning tree for a weighted, undirected graph (with not necessarily distinct weights) then for any minimum spanning tree $T$ there is another minimum spanning tree $T'$ that differs from $T$ in only one edge (so, when $T$ and $T'$ are considered as sets of edges, $\mid T \setminus T'\mid = \mid T' \setminus T\mid = 1$).
Problem : Give an efficient algorithm to determine if a given minimum spanning tree is unique. The inputs to your algorithm are
- $n$, the number of vertices in the graph (the vertices are then numbered $0, \ldots, n-1$);
- the set of edges in the graph, as an adjacency list or adjacency matrix (specify which one you are using);
- a subset $T$ of the edges that forms a minimum spanning tree, using the same data structure as the complete set of edges.