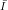 ” on the
right side of the definition of g is
” on the
right side of the definition of g is 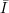 , not I, but it takes sharp eyes to spot the difference in the printed version
of the book. Here,
, not I, but it takes sharp eyes to spot the difference in the printed version
of the book. Here, 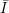 is intended to denote the set difference {1,2,…,|x|}- I.
is intended to denote the set difference {1,2,…,|x|}- I.
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 461b: Foundations of Cryptography | Handout #4 | |
| Professor M. J. Fischer | February 19, 2009 | |
Problem Set 2
Due in class on Thursday, February 26, 2009.
Problem 1 One-way functions and collections of one-way functions
[Textbook, Chapter 2, Exercise 18.]
Problem 2 Hard core of one-way function
[Textbook, Chapter 2, Exercise 24, as modified below.]
Note that the “Guideline” is poorly printed and easy to misinterpret. The second subscript “x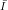 ” on the
right side of the definition of g is
” on the
right side of the definition of g is 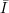 , not I, but it takes sharp eyes to spot the difference in the printed version
of the book. Here,
, not I, but it takes sharp eyes to spot the difference in the printed version
of the book. Here, 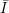 is intended to denote the set difference {1,2,…,|x|}- I.
is intended to denote the set difference {1,2,…,|x|}- I.
Also, we are used to dealing with functions on strings, yet the guideline defines g to take a set
argument. There are many ways of representing finite sets by strings. For this problem, represent the set
I ⊆{1,2,…,|x|} by the length-|x| bit-vector u, where ui = 1 iff i  I. It follows that
I. It follows that 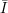 is represented by
¬u, the bitwise complement of u.
is represented by
¬u, the bitwise complement of u.
Finally, we define x[u] = xi1…xik, where ij is the position of the jth 1-bit in u, and k is the number of 1-bits in u. Thus, if u represents the set S, then x[u] denotes the string xS defined in the guideline.
Using these conventions, the intended function g is defined by
![g(x,u ) = (f(x[u]),x [¬u ],u).](ho044x.png)
You may ignore the part of the guideline that talks about more “dramatic” predictability.
Amplification is the technique for reducing errors in probabilistic algorithms by repeating the computation many times. We have used amplification both for reducing the error probability in algorithms attempting to invert one-way functions and also for increasing the advantage of algorithms attempting to guess hard core predicates. However, the way it is used differs markedly in the two cases.
For inverting functions, we assume an algorithm A(y) succeeds with probability at least ϵ(n) at
returning a value x  f-1(y). To amplify, we repeat A(y) for r(n) times and succeed if any
of the runs succeed. This depends on our ability to feasibly test whether the value returned
by A(y) in a given run is correct or not. Hence, the amplified success probability is at least
f-1(y). To amplify, we repeat A(y) for r(n) times and succeed if any
of the runs succeed. This depends on our ability to feasibly test whether the value returned
by A(y) in a given run is correct or not. Hence, the amplified success probability is at least
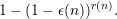
For guessing the value of a hard core predicate, we assume an algorithm D(y) with advantage ϵ(n) at predicting b(x). To amplify, we repeat D(y) for r(n) times. Because we do knot know which runs of D(y) return correct answers, we select our final answer to be the majority of all returned answers. The advantage of the resulting algorithm D′ is not easy to compute directly, so we use the Chernoff bound or other statistical techniques to get a lower bound on it.
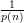 .
.