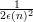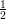YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 461b: Foundations of Cryptography | Handout #6 |
| Yitong Yin | | March 1, 2009 |
|
|
|
| |
Solutions to Problem Set 2
Originally due Thursday, February 26, 2009.
Problem 1 One-way functions and collections of one-way functions
[Textbook, Chapter 2, Exercise 18.]
Solution
- The sampling algorithm (I,D) on input 1n can be seen as a function mapping q(n) bits (the
internal coin tosses) to a pair (i,x), where q(n) is polynomial of n (number of internal coin
tosses), i

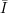 ∩{0,1}n and x
∩{0,1}n and x  Di. Denoting this function as Sn, it is easy to see that
Di. Denoting this function as Sn, it is easy to see that
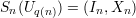
where In is the output distribution of algorithm I on input 1n, and Xn is the output of
algorithm D on input In.
A new function g can be defined as such: for each z  {0,1}q(n), represent that Sn(z) =
(i,x), thus g(z) = (i,fi(x)). It also follows that g(Uq(n)) = (In,fIn(Xn)).
{0,1}q(n), represent that Sn(z) =
(i,x), thus g(z) = (i,fi(x)). It also follows that g(Uq(n)) = (In,fIn(Xn)).
We will show that the above g is a one-way function.
Function g is polynomial-time computable since Sn can be computed by the polynomial-time
algorithms I and D and fi can be computed by the polynomial-time algorithm F .
Suppose that g is polynomial-time invertable, namely, there exists a polynomial-time
algorithms A such that for some polynomial p(n),
![Pr[A(1q(n),g(Uq(n))) ∈ g-1(g(Uq(n)))] ≥--1- .
p (n )](ho062x.png)
Define a new algorithm B as such: for each input y = (i,fi(x)) where i 
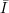 ∩{0,1}n and
x
∩{0,1}n and
x  Di, represent that Sn(A(1q(n),y)) = (j,z), where j
Di, represent that Sn(A(1q(n),y)) = (j,z), where j  {0,1}n and such that B(y) = z.
We show that B inverts the collection (I,D,F).
{0,1}n and such that B(y) = z.
We show that B inverts the collection (I,D,F).
Since g(Uq(n)) = (In,fIn(Xn)), the event that A(1q(n),g(Uq(n)))  g-1(g(Uq(n)))
is equivalent to the event that A(1q(n),(In,fIn(Xn)))
g-1(g(Uq(n)))
is equivalent to the event that A(1q(n),(In,fIn(Xn)))  g-1(In,fIn(Xn)), which
according to the definition of B, holds only if B(In,fIn(Xn))
g-1(In,fIn(Xn)), which
according to the definition of B, holds only if B(In,fIn(Xn))  f-1(fIn(Xn)). Therefore,
f-1(fIn(Xn)). Therefore,
which is contra to the assumption that (I,D,F) is a one-way collection.
- Given a one-way function f, a one-way collection (I,D,F) can be defined as such: I(1n) always
outputs 0n, D(0n) samples uniformly over the domain of f, and F(0n,x) = f(x).
Problem 2 Hard core of one-way function
[Textbook, Chapter 2, Exercise 24, as modified below.]
Note that the “Guideline” is poorly printed and easy to misinterpret. The second subscript “x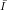 ” on the
right side of the definition of g is
” on the
right side of the definition of g is 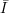 , not I, but it takes sharp eyes to spot the difference in the printed version
of the book. Here,
, not I, but it takes sharp eyes to spot the difference in the printed version
of the book. Here, 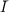 is intended to denote the set difference {1,2,…,|x|}- I.
is intended to denote the set difference {1,2,…,|x|}- I.
Also, we are used to dealing with functions on strings, yet the guideline defines g to take a set
argument. There are many ways of representing finite sets by strings. For this problem, represent the set
I ⊆{1,2,…,|x|} by the length-|x| bit-vector u, where ui = 1 iff i  I. It follows that
I. It follows that 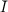 is represented by
¬u, the bitwise complement of u.
is represented by
¬u, the bitwise complement of u.
Finally, we define x[u] = xi1…xik, where ij is the position of the jth 1-bit in u, and k is the number
of 1-bits in u. Thus, if u represents the set S, then x[u] denotes the string xS defined in the
guideline.
Using these conventions, the intended function g is defined by
![g(x,u ) = (f(x[u]),x [¬u ],u).](ho069x.png)
You may ignore the part of the guideline that talks about more “dramatic” predictability.
Solution
We take the function g(x,u) = (f(x[u]),x[¬u],u) defined in the problem guideline. For each input (x,u),
let bi(x,u) denote the ith bit of the input.
Let Ai be such an algorithm: for each input in the form of (f(x[u]),x[¬u],u) if i > |u|
(size of the set u), return the (i -|u|)th bit of the binary representation of u; if i ≤|u| and
i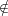 u, return xi which is contained in x[¬u]; and if otherwise, flip a fair coin and return the
outcome.
u, return xi which is contained in x[¬u]; and if otherwise, flip a fair coin and return the
outcome.
It is easy to see that it always holds that Ai(g(x,u)) = bi(x,u) for i > |u|, i.e. Pr[Ai(g(Un)) = bi(x,u)] = 1
for i > |u|.
For i ≤|u|, Ai(g(x,u)) = bi(x,u) when i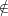 u, or if i
u, or if i  u and Ai makes a correct guess. According to
the total probability, for i ≤|u|,
u and Ai makes a correct guess. According to
the total probability, for i ≤|u|,
where u is a uniform random string of length |x|, thus Pr[ui = 1] = Pr[ui = 0] = 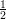 . The above probability
is 3∕4.
. The above probability
is 3∕4.
Problem 3 Amplification
Amplification is the technique for reducing errors in probabilistic algorithms by repeating the
computation many times. We have used amplification both for reducing the error probability in algorithms
attempting to invert one-way functions and also for increasing the advantage of algorithms
attempting to guess hard core predicates. However, the way it is used differs markedly in the two
cases.
For inverting functions, we assume an algorithm A(y) succeeds with probability at least ϵ(n) at
returning a value x  f-1(y). To amplify, we repeat A(y) for r(n) times and succeed if any
of the runs succeed. This depends on our ability to feasibly test whether the value returned
by A(y) in a given run is correct or not. Hence, the amplified success probability is at least
f-1(y). To amplify, we repeat A(y) for r(n) times and succeed if any
of the runs succeed. This depends on our ability to feasibly test whether the value returned
by A(y) in a given run is correct or not. Hence, the amplified success probability is at least
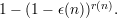
For guessing the value of a hard core predicate, we assume an algorithm D(y) with advantage ϵ(n) at
predicting b(x). To amplify, we repeat D(y) for r(n) times. Because we do knot know which runs of D(y)
return correct answers, we select our final answer to be the majority of all returned answers. The advantage
of the resulting algorithm D′ is not easy to compute directly, so we use the Chernoff bound or other
statistical techniques to get a lower bound on it.
Questions:
Suppose ϵ(n) = 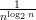 =
= 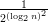 .
.
- Show that for all positive polynomials p(⋅) and all sufficiently large n that ϵ(n) <
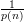 .
.
- Suppose ϵ(n) is the success probability for algorithm A. Find as small a function r(n) as you
can such that repeating A for r(n) times results in a success probability greater than 1∕2 for
all sufficiently large n.
- Suppose ϵ(n) is the advantage of algorithm D. Find as small a function r(n) as you can such
that repeating D for r(n) times and taking the majority gives an advantage greater than 1∕4
for all sufficiently large n.
Solution
- Let LHS(n) = -log 2ϵ(n) = (log 2n)2, and RHS(n) = -log 2p(n). Since p(⋅) is a
polynomial, RHS(n) ≥ C log 2n for some constant C which is independent of n.
For all n > 2C, it holds that log 2n > C, thus RHS(n) = (log 2n)2 < C log 2n ≤
RHS(n). Since -log 2(⋅) is monotonically decreasing, it must holds all the above n that
ϵ(n) = 2-LHS(n) < 2-RHS(n) = 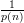 .
.
- Since the runnings of algorithm are independent, the probability that all r = r(n) trails fail is
(1 - ϵ)r. We want this probability to be less than 1∕2. To have (1 -ϵ)r < 1∕2, it requires that exp
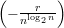 < 1∕2. Solving this inequality we have that
r(n) > nlog 2n ⋅ ln2.
< 1∕2. Solving this inequality we have that
r(n) > nlog 2n ⋅ ln2.
- Let Xi be the random variable which indicates ith trial of D succeeds, it holds that Xi = 1 with
probability
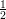 + ϵ and Xi = 0 with probability
+ ϵ and Xi = 0 with probability 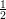 - ϵ. The probability that the majority fails is
The advantage is 1∕4, thus the probability that bad thing happens is less than 1∕2 - 1∕4 = 1∕4
i.e. q < 1∕4. To make q <
- ϵ. The probability that the majority fails is
The advantage is 1∕4, thus the probability that bad thing happens is less than 1∕2 - 1∕4 = 1∕4
i.e. q < 1∕4. To make q < 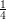 , it requires that r(n) > (
, it requires that r(n) > (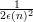 - 2)ln8 = (
- 2)ln8 = (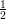 n2 log 2n - 2)ln8.
n2 log 2n - 2)ln8.

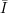 ∩{0,1}n and x
∩{0,1}n and x  Di. Denoting this function as Sn, it is easy to see that
Di. Denoting this function as Sn, it is easy to see that
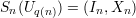
 {0,1}q(n), represent that Sn(z) =
(i,x), thus g(z) = (i,fi(x)). It also follows that g(Uq(n)) = (In,fIn(Xn)).
{0,1}q(n), represent that Sn(z) =
(i,x), thus g(z) = (i,fi(x)). It also follows that g(Uq(n)) = (In,fIn(Xn)).
![Pr[A(1q(n),g(Uq(n))) ∈ g-1(g(Uq(n)))] ≥--1- .
p (n )](ho062x.png)

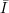 ∩{0,1}n and
x
∩{0,1}n and
x  Di, represent that Sn(A(1q(n),y)) = (j,z), where j
Di, represent that Sn(A(1q(n),y)) = (j,z), where j  {0,1}n and such that B(y) = z.
We show that B inverts the collection (I,D,F).
{0,1}n and such that B(y) = z.
We show that B inverts the collection (I,D,F).
 g-1(g(Uq(n)))
is equivalent to the event that A(1q(n),(In,fIn(Xn)))
g-1(g(Uq(n)))
is equivalent to the event that A(1q(n),(In,fIn(Xn)))  g-1(In,fIn(Xn)), which
according to the definition of B, holds only if B(In,fIn(Xn))
g-1(In,fIn(Xn)), which
according to the definition of B, holds only if B(In,fIn(Xn))  f-1(fIn(Xn)). Therefore,
f-1(fIn(Xn)). Therefore,
![Pr[B (I ,f (X ))]
nq(n)In n - 1
≥ Pr[A (1 ,g(Uq(n))) ∈ g (g (Uq (n)))]
-1--
≥ p(n),](ho064x.png)
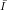 ” on the
right side of the definition of
” on the
right side of the definition of 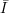 , not
, not 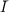 is intended to denote the set difference
is intended to denote the set difference 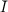 is represented by
is represented by
![g(x,u ) = (f(x[u]),x [¬u ],u).](ho069x.png)
![Pr[Ai(g(Un )) = bi(x,u)]
= Pr[the outcom e of coin flipp ing is 1]Pr[ui = 1]+ 1 ⋅Pr[ui = 0]
= 1-Pr[ui = 1]+ Pr[ui = 0]
2](ho0612x.png)
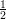 . The above probability
is
. The above probability
is 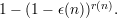
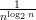
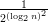 .
.
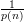 .
.
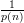 .
.
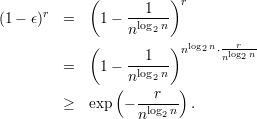
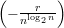
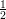
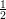
![[ r ]
1-∑ 1-
Pr r ≤ 2
[ i=1 ( ) ]
1-∑r 1-
= Pr r - 2 + ϵ ≤ - ϵ
[| i=1 ( ) | ]
||1 ∑r 1 ||
≤ Pr ||r- - 2 + ϵ || ≥ ϵ
( i=1 )
- ϵ2r
≤ 2 exp (1-----2) (due to C herno ff bou nd)
2 - 2ϵ
= q.](ho0623x.png)
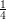 , it requires that
, it requires that