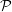4 Turing Machine Descriptions and Simulations

4.1 Universal Turing machines

Each Turing machine has a finite description. A usual treatment of Turing machines develops a description language for Turing machines whereby a machine M is uniquely described by a string e_M. There is nothing particularly remarkable about Turing machine programs compared to C programs or any other familiar programming language. The important property is that given a Turing machine program e_M, you can “run” the program and see what it does on a particular input string.

More precisely, there is a Turing machine U, called a universal machine, such that for every Turing machine M, if e_M describes M, then U(e_M,x) and M(x) are the same, meaning that either both halt and give the same outputs, or neither halts. Moreover, there is a fixed polynomial function p(t,e,x) such that Time_U(e_M,x) ≤ p(Time_M(x),e_M,x). Thus, not only can U simulate any other Turing machine, but there is at most a polynomial time slowdown in the simulation. Hence, if M(x) runs in polynomial time, then so does U(e_M,x).

4.2 What can we do with a program?

A natural question is, “What we can tell from looking at a program?” The short answer is “nothing” except for what can be learned by simulating it step by step. The famous theorem about the unsolvability of the halting problem says that there is no algorithm (Turing machine) H(e_m) that always halts and correctly outputs 1 if M(e_M) halts and 0 if M(e_M) does not halt. Thus, one cannot look at a program and in a finite amount of time say for sure whether or not that program will halt when given its own description as input.

Many other surprising results are known as well. For example, given a program e_M, you can’t even find another program e_M′ that is guaranteed to differ from e_M. No matter how you try to modify the code of e_M, you might just end up with an equivalent program.

On the positive side, there exists a Turing machine M such that M(␣) = e_M, that is, M when run on a blank tape, writes its own description on the tape and then halts. This is true for any reasonable programming language and does not depend on special features of the language – only that it is adequately powerful to describe any algorithm.

As a fun exercise, you can try to write a C program self.c, such that, when compiled and run, the text written to standard output is identical to the contents self.c. Of course, you could write a program that opened self.c and copied it to standard output, but the program I have in mind doesn’t cheat and will work correctly even if the source file is deleted before the executable is run.

5 A Hard Problem

Our interest in Turing machines and time complexity is to allow us to distinguish “feasible” from “infeasible” computations. We have already said that we regard anything computable in polynomial time as being feasible to compute, so the membership problem for all languages in 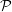is feasible. On the other hand, we need problems that are infeasible for cryptography. For example, we want it to be infeasible for an adversary to recover the plaintext of a message from its ciphertext.

We now show that hard problems really do exist. We do this by diagonalization. We’ll begin with a construction that almost works and then show how to fix it to give us the function of theorem 1.

The following is an immediate corollary since p(n) ≤ 2ⁿ for every polynomial p(n) and all sufficiently large n.

We begin our construction by defining a function g(x) as follows: Given an input string x, determine whether or not x is a syntactically valid description of some Turing machine M. If not, halt and output g(x) = 0. Otherwise, use the universal machine U to simulate 2^|x| steps of M(x). Suppose M halts on x within that many steps and produces output string y. If y = 0, let g(x) = 1. If y≠0, let g(x) = 0. Either way, g(x)≠y = M(x).

Suppose M is any Turing machine that computes g. We show that M(e_M) runs for more than 2^|e_M| steps. Suppose to the contrary that M(e_M) halts in at most 2ⁿ steps and outputs y. Then by definition of g, g(e_M)≠y. But this contradicts the assumption that M (correctly) computes g.

We have thus shown that any machine M that computes g(x) must run for a long amount of time (i.e., more than 2ⁿ steps) on at least one input x, namely, on the input x = e_M. But this alone isn’t enough to conclude that M does not run in polynomial time. For that, we need a function f(x) satisfying the stronger property that any machine that computes f(x) runs for more than 2ⁿ steps on infinitely many inputs x of length n.

A very slight modification of the above construction gives us the desired function f(x). Let γ(x) be a polynomial-time computable function such that for every string z, there are infinitely many x such that γ(x) = z. Given an input string x, compute z = γ(x) and determine whether or not z is a syntactically valid description of some Turing machine M. If not, halt and output f(x) = 0. Otherwise, use the universal machine U to simulate 2^|x| steps of M(x). Suppose M halts on x within that many steps and produces output string y. If y = 0, let f(x) = 1. If y≠0, let f(x) = 0.¹

Now, suppose M is any Turing machine that computes f. Then by an argument similar to that above for g(x), we show that M(x) runs for more than 2^|x| steps for every input x for which γ(x) = e_M. Suppose to the contrary that M on such an input x halts in at most 2^|x| steps and outputs y. Then by definition of f, f(x)≠y. But this contradicts the assumption that M (correctly) computes f.

It remains to describe how to build such a function γ. A pairing system is a collection of three polynomial-time computable functions ρ, π₁, and π₂ such that

1. ρ is a 1-1 mapping from pairs of strings to strings.
2. The projection functions π₁ and π₂ satisfy π₁(ρ(u,v)) = u and π₂(ρ(u,v)) = v.

Given a pairing system, we define γ(x) = π₁(x). This has the desired properties since for every x such that x = ρ(z,v) we have γ(x) = π₁(x) = z, and there are infinitely many such x as v varies over all possible values.

Finally, we must construct a pairing system. Many are possible, but one simple one is to define ρ′(x,y) = x2y as a string over the 3-letter alphabet {0,1,2} and then define ρ(x,y) = σ(ρ′(x,y)), where σ encodes each letter of the new alphabet as pairs of bits, so ‘0’ is encoded as 00, ‘1’ as 01, and ‘2’ as 10. Thus, ρ(01,101) = σ(012101) = 000110010001.

6 An Alternative View of

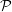
In section 3.5, we define the class 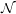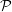(for “non-deterministic polynomial time) as those languages whose members have short, easily checkable witnesses. We now give an alternative view in terms of non-deterministic Turing machines.

A configuration of a Turing machine is the complete description of the progress of a computation, including the entire contents of the non-blank portion of the tape, the current head position, and the internal state of the Turing machine’s finite memory. One can imagine an infinite graph G where the nodes are all possible Turing machine configurations, and two nodes u and v are connected by a directed edge (u,v) iff the Turing machine, when started in configuration u, reaches configuration v in one step. This graph has out-degree at most one. Halting nodes have no outgoing edges; non-halting nodes have a single outgoing edge.

A Turing machine can be thought of as a device that constructs a path in G starting from the initial configuration. The path terminates in a halting configuration if the machine halts; otherwise, the path is infinite.

A non-deterministic Turing machine is the same as a (deterministic) Turing machine except that a node u in the configuration graph can have two outgoing edges (u,v₁) and (u,v₂). This arises when the machine has a choice of two possible next moves; namely, it can choose to go to v₁ or to v₂. We do not specify how the machine makes such a choice, so a non-deterministic machine is not a “machine” in the usual sense of something that could be implemented in the real world. Rather, think of its actions as being incompletely specified, so in certain configurations, it can take either of two possible actions. (This is as if C programs had a construct choose {<block1>} or {<block2>}.)

The graph G of a non-deterministic Turing machine M can have many different paths starting from the initial configuration, and each of these is a possible “computation” of the machine. We say that an input x is accepted by M in at most t steps if there exists a path in G of length at most t from the initial configuration of M on input x to some halting configuration. The set of all x that are accepted by M (in any number of steps) is the language L_M accepted by M.

We say that a language L is in 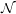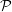if there is a non-deterministic Turing machine M and a polynomial p(n) such that M accepts every x L in at most p(|x|) steps, and M does not accept any x ⁄ L (in any number of steps).

To relate this to the definition given in section 3.5, we externalize the choices made by a non-deterministic machine. Imagine we give M a second input string y which we call a choice sequence. Every time M has a choice to make, it reads the next bit of y and makes the first or second possible choice depending on that bit. This turns M into an ordinary deterministic Turing machine with two inputs, x and y. If the original non-deterministic machine accepts x within t steps, then there exists a choice sequence y of length at most t such that M(x,y) halts in at most t steps. Conversely, if the non-deterministic machine does not accept x, then M(x,y) does not halt for any y. Thus, y becomes a witness to the membership of x in L, and the deterministic machine M becomes a verifier for proofs of membership in L.

There are some technical details which I won’t go into here having to do with non-halting computations, for our definitions in section 3.5 assume that the relation R_L is computable in deterministic polynomial time, which means that the machine computing it always halts within the allowed time bound and correctly answers whether or not R_L(x,y) is true. However, this isn’t a serious difference, for given a machine M(x,y) that either halts in at most p(|x| + |y|) steps for some polynomial p(n) or never halts, we can convert it into a machine that always halts by first computing t = p(|x| + |y|) and then simulating the original machine for t steps. If the original machine halts within that time bound, the new machine halts and says true. If not, the new machine halts and says false.

The notion of splitting a non-deterministic computation into a deterministic part and a choice sequence becomes particularly convenient in the next section where we consider probabilistic Turing machines – machines with choices where the choices are made according to random flips of an unbiased coin.