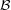

 ⊆
⊆ ∕poly
∕polyYALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 461b: Foundations of Cryptography | Notes 4 (rev. 2) | |
| Professor M. J. Fischer | January 22, 2009 | |
Lecture Notes 4
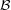

 ⊆
⊆ ∕poly
∕polyWe supply the missing piece to the proof of Theorem 4 in section 11 that 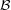

 ⊆
⊆ ∕poly. Namely, if
L
∕poly. Namely, if
L 
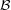

 , there exists a ppTM M′ recognizing L with error probability less than 2-n for all inputs x of
length n.
, there exists a ppTM M′ recognizing L with error probability less than 2-n for all inputs x of
length n.
Lemma 1 Let L 
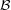

 . There is a probabilistic polynomial-time Turing machine M′ such
that
. There is a probabilistic polynomial-time Turing machine M′ such
that
 L,Pr[M′(x) = 1] > 1 - 2-|x|;
L,Pr[M′(x) = 1] > 1 - 2-|x|;
 L,Pr[M′(x) = 0] > 1 - 2-|x|.
L,Pr[M′(x) = 0] > 1 - 2-|x|.
Proof: By definition of 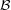

 , there exists a ppTM M that recognizes L with error probability at
most 1∕3 for each input x. We can assume without loss of generality that M always outputs either
0 or 1.
, there exists a ppTM M that recognizes L with error probability at
most 1∕3 for each input x. We can assume without loss of generality that M always outputs either
0 or 1.
Let r be an odd positive integer to be determined later. The ppTM M′ on input x of length n runs M(x) a total of r times and gives as its output the majority value among the multiset of r outputs from M. We use the Chernoff bound (see lecture 1)
![[|∑ | ]
||---Xi || - 2εp(21r-p)-
P r | r - p| ≥ ε ≤ 2e .](ln040x.png) | (1) |
plus additional probabilistic reasoning to bound the error probability of M′.
Define a random variable:
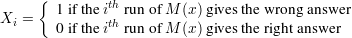
The number of wrong answers in computing M′(x) is ∑ Xi, so M′(x) gives the wrong answer iff ∑ Xi > r∕2.
We now calculate an upper bound on the error probability for M′(x). Let p be the probability that M(x) gives the wrong answer.1 By assumption, p ≤ 1∕3.
Equation 4 follows since 1∕2 - p ≥ 1∕6, and equation 5 follows since the absolute value brackets only increase the cardinality of the event.Taking ε = 1∕6 and using the fact that p(1 - p) < 2∕9, equation 1 yields
![[|∑ | ]
||---Xi || 1- -r∕16
P r | r - p| > 6 ≤ 2e .](ln043x.png) | (6) |
It is easily verified that
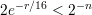 | (7) |
for all r > 16(1 + n)∕log 2e.
We now fix r to be the least odd positive integer satisfying equation 7. Combining equations 2–7 gives the desired error bound:
![P r[M ′(x) gives wrong answ er] < 2-n.](ln045x.png) | (8) |
Moreover, M′ runs in polynomial time since M does and r = O(n). This establishes the lemma. __
One-way functions are at the heart of cryptography. Intuitively, a function f : {0,1}*→{0,1}* is one-way if it is “easy” to compute and “hard” to “invert”. We next give precise technical definitions of these concepts.
Definition: The function f is strongly one-way if it satisfies the following conditions:
![′ n -1 1
P r[A (f(Un ),1 ) ∈ f (f(Un ))] < p(n).](ln046x.png) | (9) |
Intuitively, condition 2 says that any algorithm A′ that attempts to invert f has success probability less than one over any positive polynomial for all but finitely many n. Moreover, this fact remains true even when A′ is given additional information about the inverse that it is trying to find.
The notation of equation 9 is very compressed and deserves some explanation. First of all, Un is the uniformly distributed random variable on binary strings of length n. Each occurrence of Un refers to the same length-n random string x, so each occurrence of f(Un) refers to same random string y = f(x). While x is uniformly distributed among all strings of length n, y is not so distributed. We are not assuming at this point that f is length preserving or that all strings x of length n map onto y’s of the same length. Moreover, f is not assumed to be one-to-one, so Pr[f(Un) = y] = m2-n, where m is the number of length n strings that f maps to y.
Because we don’t assume f is one-to-one, the notation f-1(y) refers to a set rather than to a particular string. By definition,
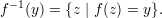
This set is called the pre-image of y. Note that if y = f(x), then x  f-1(y), but there may be other
strings in the pre-iamge as well.
f-1(y), but there may be other
strings in the pre-iamge as well.
With this background, we see that the event within the square brackets of equation 9 is the event that A′ succeeds in outputting some member of the pre-image f-1(y) for a randomly chosen string y as described above. Condition 2 then says that this probability that this event occurs is negligible (according to the definition of “negligible” in section 10). Note that A′ is not required to output the string x that was used to generate y; any string in the pre-image will do.
Note also that A′ is told the length of x as its second input. Even with this additional help, A′ has only negligible success probability. This is done to prevent functions from being considered one-way only because their inverses are too long to output in a polynomial amount of time, e.g., the function g(x) = ℓ, where ℓ is the length of x written as a binary number. For example, g(111010111) = 1001 since |111010111| = 9, and (1001)2 = 9.
Here are two obvious algorithms for inverting a function f.
Of course, to be strongly one-way, every p.p.t. algorithm A′ to invert f must have only a negligible probability of success, not just these two algorithms. But these examples provide a lower bound on what we can expect from a one-way function. In particular, no function can have an inversion success probability smaller than 2-n.
We now define a much weaker version of a one-way function. While uninteresting for cryptographic purposes, we will show that the existence of weakly one-way functions implies the existence of strongly one-way functions.
Definition: The function f is weakly one-way if it satisfies the following conditions:
![1
P r[A ′(f(Un ),1n ) ⁄∈ f-1(f(Un ))] >----.
p(n)](ln048x.png) | (10) |
Note the subtle change in the order of quantifiers and in equation 10. This says that any algorithm A′ that attempts to invert f will take a noticeable amount of the time on inputs of length n for all sufficiently large n.
A function μ(n) is noticeable if μ(n) > 1∕p(n) for some fixed positive polynomial p(⋅) and all sufficiently large n. A function cannot be both noticeable and negligible, but it is possible for a function to be neither. For example, the function μ(n) = n mod 2 that equals 1 on all odd numbers and 0 on all even numbers is neither negligible nor noticeable. It is not negligible because it fails to be smaller than 1∕p(n) for infinitely many n, where p(n) = 2. It is not noticeable because it fails to be larger than 1∕q(n) > 0 for infinitely many n and all positive polynomials q(n).