YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 461b: Foundations of Cryptography | Notes 5 (rev. 1) |
| Professor M. J. Fischer | | January 27, 2009 |
|
|
|
| |
15 Other Classes of One-Way Functions
Our definitions of strongly and weakly one-way functions are liberal in the functions that may be
considered one-way, but they are restrictive in requiring that one-way functions be hard to invert on almost
all lengths n. We explore variations in the definitions, both to achieve properties that are desirable in
practice and to gain practice in working with the definitions.
15.1 One-way functions on certain lengths
Natural candidate one-way functions might be defined only on strings of certain lengths. For
example, a graph-theoretic function that might be conjectured to be one-way might take as input
the adjacency matrix of an N-node graph, which is naturally encoded as a binary string of
length N2. Such a function would only be defined for strings whose length is a perfect square,
and we would not care what it did or whether it was hard to invert for inputs that were not
perfect squares. We are therefore led to consider functions that are defined only for certain
lengths.
Let I ⊆ ℕ -{0} be an infinite set of lengths. Define sI(n) to be the smallest integer n′ > n such that
n′ I. We say that I is polynomial-time enumerable if there is a polynomial time algorithm that on input n
writes sI(n) 1’s on its output tape and halts. It follows that sI(n) is polynomially bounded since a
polynomial-time computation cannot produce an output string that is longer than its running
time.
Note also that by excluding 0 from I, we have I = {sI(n)∣n
I. We say that I is polynomial-time enumerable if there is a polynomial time algorithm that on input n
writes sI(n) 1’s on its output tape and halts. It follows that sI(n) is polynomially bounded since a
polynomial-time computation cannot produce an output string that is longer than its running
time.
Note also that by excluding 0 from I, we have I = {sI(n)∣n  ℕ}.
ℕ}.
For example, suppose I = {n2∣n  ℕ-{0}}. Then sI(3) = 4 and sI(4) = sI(5) = sI(6) = sI(7) = sI(8) = 9.
We can compute sI(n) as follows: Test n + 1, n + 2, …, until a number m is reached that is a perfect square,
and output m in unary. This algorithm is easily seen to be computable in polynomial time since testing if a
number m is a perfect square can be done in polynomial time, and at most n numbers need to be tested
before encountering a perfect square. (More precisely, the worst case comes when n = k2 itself is a
perfect square, in which case at most (k + 1)2 - k2 = 2k + 1 = O(
ℕ-{0}}. Then sI(3) = 4 and sI(4) = sI(5) = sI(6) = sI(7) = sI(8) = 9.
We can compute sI(n) as follows: Test n + 1, n + 2, …, until a number m is reached that is a perfect square,
and output m in unary. This algorithm is easily seen to be computable in polynomial time since testing if a
number m is a perfect square can be done in polynomial time, and at most n numbers need to be tested
before encountering a perfect square. (More precisely, the worst case comes when n = k2 itself is a
perfect square, in which case at most (k + 1)2 - k2 = 2k + 1 = O(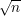 ) numbers must be
tested.)
Definition: Let I ⊆ ℕ be a polynomial-time enumerable set. The function f is strongly one-way on
lengths in I if it satisfies the following conditions:
) numbers must be
tested.)
Definition: Let I ⊆ ℕ be a polynomial-time enumerable set. The function f is strongly one-way on
lengths in I if it satisfies the following conditions:
- f is computable in polynomial time.
- For all probabilistic polynomial-time algorithms A′, all positive polynomials p(⋅), and all
sufficiently large n
 I,
I,
![′ n -1 1
P r[A (f(Un ),1 ) ∈ f (f(Un ))] < p(n).](ln051x.png) | (1) |
Definition: Let I ⊆ ℕ be a polynomial-time enumerable set. The function f is weakly one-way on lengths
in I if it satisfies the following conditions:
- f is computable in polynomial time.
- There exists a positive polynomial p(⋅) such that for all probabilistic polynomial-time algorithms A′
and all sufficiently large n
 I,
I,
![P r[A ′(f(Un ),1n ) ⁄∈ f-1(f(Un ))] >-1--.
p(n)](ln052x.png) | (2) |
Note that these definitions become identical to the respective original definitions for strongly and
weakly one-way functions if one takes I = ℕ, so they are strict generalizations of the former
concepts.
One can easily transform a strongly (weakly) one-way function f on lengths in I into an ordinary
strongly (weakly) one-way function g.
Theorem 1 Let I ⊆ ℕ be polynomial-time enumerable, and let f be strongly (weakly) one-way
on lengths in I. Define g(x) = f(x′), where x′ is the longest prefix of x such that |x′|  I, and
g(x) = 0 if x itself is shorter than any string in I. Then g is strongly (weakly) one-way.
I, and
g(x) = 0 if x itself is shorter than any string in I. Then g is strongly (weakly) one-way.
Proof: We first describe a polynomial-time algorithm to compute g. Note that m  I iff
sI(m-1) = m, so we can test membership in I in polynomial time. On input x, we test the lengths
of successively shorter prefixes x′ of x, beginning with x itself, until one is obtained that is in I
or we determine that none are in I. We then output f(x′) or 0 depending whether such a prefix is
found. This takes time O(np(n) + q(|x′|)), where p(⋅) bounds the time to compute sI and q(⋅) the
time to compute f. It follows that g can be computed in polynomial time.
I iff
sI(m-1) = m, so we can test membership in I in polynomial time. On input x, we test the lengths
of successively shorter prefixes x′ of x, beginning with x itself, until one is obtained that is in I
or we determine that none are in I. We then output f(x′) or 0 depending whether such a prefix is
found. This takes time O(np(n) + q(|x′|)), where p(⋅) bounds the time to compute sI and q(⋅) the
time to compute f. It follows that g can be computed in polynomial time.
We now show that g is hard to invert. Suppose to the contrary that there is a p.p.t. algorithm A′ and a
polynomial p(⋅) such that for infinitely many n,
![1
P r[A ′(g(Un ),1n) ∈ g-1(g(Un))] ≥---- .
p(n)](ln053x.png) | (3) |
That is, A′ successfully inverts g a noticeable amount of the time on an infinite set of lengths
I′.
We construct an algorithm A and show that it successfully inverts f a noticeable amount of
the time on an infinite subset of I. Here’s how A works. A(y,1m) runs A′(y,1n) for each n
such that m ≤ n < sI(m). Suppose A′(y,1n) produces output x′. A tests if y = f(x′), and if
so, it outputs x′ and halts. If it fails to invert f for all values of n, then it outputs failure and
halts.
Let J = {m  I∣{m,m + 1,…,sI(m) - 1}∩ I′≠∅}, that is, J consists of those m
I∣{m,m + 1,…,sI(m) - 1}∩ I′≠∅}, that is, J consists of those m  I such that the
interval [m,sI(m) - 1] includes a number n
I such that the
interval [m,sI(m) - 1] includes a number n  I′, the infinite set of lengths for which equation 3 holds.
We argue that
I′, the infinite set of lengths for which equation 3 holds.
We argue that
![P r[A(f(Um ),1m) ∈ f-1(f(Un))] ≥ P r[A′(g (Un ),1n) ∈ g-1(g(Un ))]](ln054x.png) | (4) |
holds for all m  J and n
J and n  [m,sI(m)].
[m,sI(m)].
First, we claim that f(Um) and g(Un) are identically distributed random variables. This is because if x
has length n, then the longest prefix x′ of x with |x′| I is the prefix of length m, and the length-m
prefixes of uniformly distributed strings of length n are themselves uniformly distributed. Moreover, by
definition of g, g(x) = f(x′), so the claim follows.
I is the prefix of length m, and the length-m
prefixes of uniformly distributed strings of length n are themselves uniformly distributed. Moreover, by
definition of g, g(x) = f(x′), so the claim follows.
Let y = g(x) = f(x′). A(y,1m) succeeds in inverting f on y if A′(y,1n) succeeds in inverting g on y
for any n  [m,sI(m)] since it tries them all. Hence, it’s probability of success is at least as great as that of
A(y,1n).
[m,sI(m)] since it tries them all. Hence, it’s probability of success is at least as great as that of
A(y,1n).
Finally, combining inequalities 3 and 4 gives that
![m -1 1
P r[A(f(Um ),1 ) ∈ f (f(Un))] ≥ p(n-)](ln055x.png) | (5) |
holds for all m  J ⊆ I, contradicting the hypothesis that f is strongly one-way on lengths in
I. __
J ⊆ I, contradicting the hypothesis that f is strongly one-way on lengths in
I. __
The proof for weakly one-way functions is similar and is omitted.
16 Regular and length-preserving functions
A function f on strings is length regular if |x| = |y|⇒|f(x)| = |f(y)|. Thus, the length of the argument
determines the length of the result. f is length preserving if |f(x)| = |x|.
We first remark that if the function f of Theorem 1 above is length preserving, a slight modification of
the construction of g can make it length preserving as well. Namely, if x′ is the longest prefix of x with
|x′| I, let x′′ be the remainder of x, so x = x′x′′, and define g(x) = f(x′)x′′. The proof would have to
be adjusted accordingly and is left as an exercise.
I, let x′′ be the remainder of x, so x = x′x′′, and define g(x) = f(x′)x′′. The proof would have to
be adjusted accordingly and is left as an exercise.
We now show that if f is an arbitrary strongly (weakly) one-way function, we can construct a
length-preserving strongly (weakly) one-way function f′′. We do it in two stages:
- Let p(⋅) be a polynomial such that |f(x) ≤ p(|x|). Such a p(⋅) exists since f is polynomial-time
computable. Then
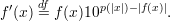 | (6) |
Clearly f′ is length regular since |f′(x)| = p(|x|) + 1 for all x.
- Let I = {p(n) + 1∣n
 ℕ}. We define f′′ on strings of lengths in I. Let |x| = p(n) + 1
ℕ}. We define f′′ on strings of lengths in I. Let |x| = p(n) + 1  I. Write
x = x′x′′, where |x′| = n and |x′′| = p(n) + 1 - n. Then
I. Write
x = x′x′′, where |x′| = n and |x′′| = p(n) + 1 - n. Then
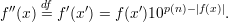 | (7) |
|f′′(x)| = |f′(x′)| = p(|x′|) + 1 = |x|, so f′′ is length regular.
The proofs that f′ and f′′ are strongly (weakly) one-way given that f is are similar to the proof of
Theorem 1 and are left as exercises.
17 Non-uniform one-way functions
A function f is non-uniformly strongly (weakly) one-way if it satisfies the definition for being
strongly (weakly) one-way, where the inverting algorithm is allowed to be a non-uniform family
{M0,M1,M2,…} of polynomial-time Turing machines with polynomial-size descriptions, or equivalently,
a family of polynomial-size circuits {Cn}n ℕ. One can show that anything computed by a Turing
machine in polynomial time can also be computed by a non-uniform family of polynomial-time
polynomial-size Turing machine or by a polynomial-size family of circuits. As a result, we have:
ℕ. One can show that anything computed by a Turing
machine in polynomial time can also be computed by a non-uniform family of polynomial-time
polynomial-size Turing machine or by a polynomial-size family of circuits. As a result, we have:
Theorem 2 If f is non-uniformly strongly (weakly) one-way, then f is strongly (weakly) one-way.
The converse is not known, and there remains the possibility that strongly (weakly) one-way functions exist but
non-uniformly strongly (weakly) one-functions do not.
It is also conceivable that weakly one-way functions exist but strongly one-way functions do not.
However, we prove that is not the case, which will be the next topic.
 I. We say that I is polynomial-time enumerable if there is a polynomial time algorithm that on input n
writes sI(n) 1’s on its output tape and halts. It follows that sI(n) is polynomially bounded since a
polynomial-time computation cannot produce an output string that is longer than its running
time.1
Note also that by excluding 0 from I, we have I = {sI(n)∣n
I. We say that I is polynomial-time enumerable if there is a polynomial time algorithm that on input n
writes sI(n) 1’s on its output tape and halts. It follows that sI(n) is polynomially bounded since a
polynomial-time computation cannot produce an output string that is longer than its running
time.1
Note also that by excluding 0 from I, we have I = {sI(n)∣n  ℕ}.
ℕ}.
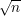
![′ n -1 1
P r[A (f(Un ),1 ) ∈ f (f(Un ))] < p(n).](ln051x.png)
![P r[A ′(f(Un ),1n ) ⁄∈ f-1(f(Un ))] >-1--.
p(n)](ln052x.png)
![1
P r[A ′(g(Un ),1n) ∈ g-1(g(Un))] ≥---- .
p(n)](ln053x.png)
![P r[A(f(Um ),1m) ∈ f-1(f(Un))] ≥ P r[A′(g (Un ),1n) ∈ g-1(g(Un ))]](ln054x.png)
![m -1 1
P r[A(f(Um ),1 ) ∈ f (f(Un))] ≥ p(n-)](ln055x.png)