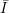 and a family of functions
{fi}i
and a family of functions
{fi}i
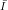 . For each i
. For each i 
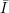 , the domain of fi is a finite set Di.
, the domain of fi is a finite set Di.
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 461b: Foundations of Cryptography | Notes 8 (rev. 1) | |
| Professor M. J. Fischer | February 5, 2009 | |
Lecture Notes 8
Although we have defined one-way functions on the infinite domain of all binary strings, for cryptographic applications we are often interested in strings of of a fixed length n, where n is determined by a security parameter. We have already seen in section 15.1 of lecture 5 that a one-way function defined only on lengths in a set I can be used to build a one-way function defined on all lengths, provided that I is polynomial-time enumerable. Intuitively, this just means that I is not too sparse and there are feasible algorithms for enumerating I and deciding membership in I—all the things you would expect from a “nice” set, for example, the set of all even numbers.
Later, when we want to talk about trapdoor functions, we’ll again need to consider lengths separately, since a trapdoor string (think RSA private key for now) only works for a finite set of inputs (the numbers in Z* n for RSA). Because of this, we shift gears slightly and consider infinite collections of finite functions instead of a single infinite functions.
Definition: A collection of functions consists of an infinite set of indices 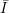 and a family of functions
{fi}i
and a family of functions
{fi}i
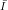 . For each i
. For each i 
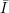 , the domain of fi is a finite set Di.
, the domain of fi is a finite set Di.
For cryptographic applications, we need some additional properties. Namely, given an index
(description) i 
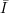 , we need to be able to compute fi(x) given i
, we need to be able to compute fi(x) given i 
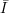 and x
and x  Dn. In addition, we need to
be able to be able to randomly sample (not necessarily uniformly) from both
Dn. In addition, we need to
be able to be able to randomly sample (not necessarily uniformly) from both 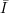 ∩{0,1}n and
fromDi.
∩{0,1}n and
fromDi.
Definition: A collection of functions 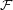 = {fi}i
= {fi}i
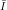 indexed by
indexed by 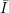 is said to be useful if there are
probabilistic polynomial-time algorithms I and D and deterministic algorithm F that satisfy the
following:
is said to be useful if there are
probabilistic polynomial-time algorithms I and D and deterministic algorithm F that satisfy the
following:
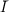 ∩{0,1}n.
∩{0,1}n.

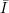 is a random variable ranging over Di.
is a random variable ranging over Di.

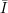 and x
and x  Di.
Di.We say that 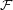 is described by
is described by 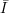 , I, D, and F .
, I, D, and F .
Now we can define the strongly one-way property for useful collections of functions.
Definition: Let 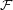 be a useful collection of functions described by
be a useful collection of functions described by 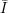 , I, D, and F . We say
, I, D, and F . We say 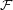 is
strongly one-way if for every probabilistic polynomial-time algorithm A′, every positive polynomial
p(⋅), and all sufficiently large n,
is
strongly one-way if for every probabilistic polynomial-time algorithm A′, every positive polynomial
p(⋅), and all sufficiently large n,
![P r[A ′(In,fI (Xn)) ∈ f-1(fI (Xn ))] <--1- ,
n In n p(n )](ln0813x.png)
where In is the random variable I(1n), and Xn is the random variable D(In). Following the usual convention, all occurrences of In refer to the same randomly chosen value i = I(1n), so in particular, In and Xn are not assumed to be independent; rather, Xn = D(i) for the chosen i.
In words, an experiment consists of choosing random values i = I(1n) and x = D(i) using the
probabilistic algorithms I and D, computing y = F(i,x), and choosing random x′ = A′(i,y).
The experiment is said to succeed if and only if F(i,x′) = y. The strongly one-way property
requires that the overall probability of success of an experiment be at most 1∕p(n). Note that this
probability is averaged over several sources of randomness: the choice of i, the choice of x, and
the randomness in the algorithm A′. Because the requirement is only on the average success
probability, it does not preclude higher success probabilities for particular values of i 
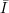 or
x
or
x  Di.
Di.
RSA collection of functions
The index set 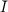 consists of pairs (N,e), where N = PQ for distinct primes P , Q of equal length and
e
consists of pairs (N,e), where N = PQ for distinct primes P , Q of equal length and
e  Z*N. For i = (N,e)
Z*N. For i = (N,e) 
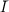 , we have Di = Z*N and fi(x) = xe (mod N).
, we have Di = Z*N and fi(x) = xe (mod N).
To show that the RSA collection satisfies the definition for a useful collection of functions, we
must give algorithms IRSA, DRSA, and FRSA. Briefly, IRSA(1n) selects uniformly distinct
primes P and Q of length n, sets N = PQ, selects uniformly an integer e  Z*N, and returns
the pair (N,e). Algorithm DRSA((N,e)) simply selects uniformly an element from Z*N.
FRSA((N,e),x) = xe (mod N). All three of these algorithms were presented in CPSC 467 in the
context of RSA. IRSA is the key generation algorithm, which also uses the algorithm DRSA for
sampling from Z*N in order to select e. FRSA is the algorithm for computing the RSA encryption
function.
Z*N, and returns
the pair (N,e). Algorithm DRSA((N,e)) simply selects uniformly an element from Z*N.
FRSA((N,e),x) = xe (mod N). All three of these algorithms were presented in CPSC 467 in the
context of RSA. IRSA is the key generation algorithm, which also uses the algorithm DRSA for
sampling from Z*N in order to select e. FRSA is the algorithm for computing the RSA encryption
function.
It is an open problem if RSA is strongly one-way, or even if it is as hard to invert as factoring, but no feasible algorithm for inverting it has yet been discovered.
Other collections See the textbook for other examples of one-way collections, namely, the Rabin Function, the Factoring Permutations, and Discrete Logarithms.
A collection of strongly one-way trapdoor permutations is similar to the collection of strongly one-way
functions defined in section 20.1, except that the functions are required to be permutations (i.e.,
one-to-one and onto), and the index set is expanded to include the index of an algorithm for
computing the inverse f-1(y) = x. Namely, 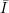 =
= 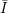 1 ×
1 ×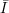 2, where
2, where 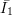 is the set of indices of
permutations in the collection, and
is the set of indices of
permutations in the collection, and 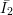 is the set of indices of the inverses of functions in the
collection.
is the set of indices of the inverses of functions in the
collection.
The algorithm I(1n) returns a pair (i,t) 
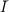 1 ×
1 ×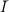 2, where i has length n, and t has length
polynomial in n. The index i describes a permutation fi in the collection and is interpreted by
the algorithm F as before, namely, F(i,x) = fi(x) for all x
2, where i has length n, and t has length
polynomial in n. The index i describes a permutation fi in the collection and is interpreted by
the algorithm F as before, namely, F(i,x) = fi(x) for all x  Di. The index t describes the
inverse fi-1 of fi and is interpreted by a fourth required algorithm, F-1, with the property that
F-1(t,y) = fi-1(y).
Di. The index t describes the
inverse fi-1 of fi and is interpreted by a fourth required algorithm, F-1, with the property that
F-1(t,y) = fi-1(y).
See the textbook for more details as well as variations on this definition that allow the required algorithms to have small probability of failure (as for example the RSA key generation algorithm does in the unlikely case that the probabilistic primality test fails and uses a non-prime for P or Q).
Example
The RSA collection of functions is easily extended to the RSA collection of trapdoor permutations.
Namely, 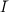 2 consists of pairs (N,d), and IRSA(1n) = ((N,e),(N,d)), where (N,e) is the public RSA key,
(N,d) is the private key, and F-1((N,d),y) = yd (mod N).
2 consists of pairs (N,d), and IRSA(1n) = ((N,e),(N,d)), where (N,e) is the public RSA key,
(N,d) is the private key, and F-1((N,d),y) = yd (mod N).
Let f be a strongly one-way function. By definition, no algorithm can invert f with a non-negligible success probability, but this doesn’t preclude algorithms that can “partially” invert f in the sense of recovering a lot of information about the inverse. For example, we observed earlier that if f is strongly one-way, then so is
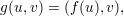
where |u| = |v|, even though given y = (f(u),v), we can easily recover half of the bits of an x′ = (u′,v′) for which f(x′) = y, namely, we know that y′ = y.
We’d like to know the answers to questions such as the following:
To begin thinking about these questions, we define the notion of a “hard-core” predicate b of a strongly
one-way function f. The idea is that b is a predicate that depends on x, but b cannot be predicted with better
than 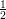 + ε accuracy given only y = f(x).
+ ε accuracy given only y = f(x).
There are two reasons why this might be the case. One is that if f is not one-to-one, then f loses
information, so we might have y = f(x′) = f(x′′) for x′≠x′′, yet b(x′)≠b(x′′). In this case, our chance of
correctly guessing b given y is exactly 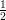 , since it is equiprobable given y whether x = x′ or
x = x′′.
, since it is equiprobable given y whether x = x′ or
x = x′′.
On the other hand, if f is one-to-one, then the only thing that makes b hard to compute is if f is hard to invert. Hence, we are primarily interested in the case of functions f that are both strongly one-way and also one-to-one. Nevertheless, we state the definition of hard-core in the more general form without the requirement that f be 1-1.
Definition: Let f be a function. A polynomial-time computable predicate b : {0,1}*→{0,1} is a hard core of f if, for every probabilistic polynomial-time algorithm A′, every positive polynomial p(⋅), and all sufficiently large n,
![Pr[A ′(f(Un )) = b(Un)] < 1+ -1--.
2 p(n )](ln0828x.png)
Given any such algorithm A′, we define the advantage of A′ (at predicting b(x) given f(x)) to be the quantity
![εA ′(n) = P r[A ′(f(Un )) = b(Un)]- 1-
2](ln0829x.png)
Thus, b is a hard core of f if εA′(n) is a negligible function for every p.p.t. algorithm A′.
Our goal in the next two lectures is to prove the theorem
Theorem 1 If strongly one-way functions exist, then there exists a strongly one-way function that has a hard-core predicate.
We proceed by considering strongly one-way functions g of a special kind. Let f be strongly one-way and length-preserving. For |x| = |r|, define
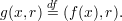
Proof: The fact that g is strongly one-way on even lengths is obvious, since the first half x of any inverse (x,r) of g(y,r) is also an inverse of f(y). Hence, an algorithm F to invert f, given an algorithm G for inverting g, merely guesses a string r of the same length as y, computes (x′,r′) = G(y,r), and outputs x′. Algorithm F has the same success probability at inverting f given y as algorithm G has at inverting g given y and r. Since F has negligible success probability, then so does G; hence, g is strongly one-way (on even lengths) since f is strongly one-way.1 ___
For |x| = |r|, define the predicate
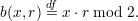
Here, x ⋅ r is the ordinary vector dot product when the strings x and r are regarded as bit vectors. More
formally, if xi and ri denote the ith bits of x and r, respectively, then x ⋅ r = ∑
i=1nxiri, and
x ⋅ r mod 2 = 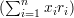 mod 2. This can be expressed using the Boolean operators ∧ (“and”) and ⊕
(“exclusive-or”):
mod 2. This can be expressed using the Boolean operators ∧ (“and”) and ⊕
(“exclusive-or”):
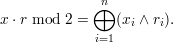
The general outline of the proof is similar to the proof that a strongly one-way function can be constructed from a weakly one-way function. Namely, we assume that b is not a hard core of g, so there is an algorithm G for predicting b with a non-negligible advantage εG(n). Using G, we construct an algorithm A for inverting f. We then analyze the success probability of F and show that it is non-negligible. This contradicts the assumption that f is strongly one-way, from which we conclude that b really is a hard core of g.