27 Statistical Closeness

Let X = {X_n}_nℕ, Y = {Y _n}_nℕ be probability ensembles. X, Y are statistically close if their statistical difference Δ(n) is negligible, where

Here’s the proof that I only sketched in class.

Proof: We prove the contrapositive. Suppose X, Y are not indistinguishable in polynomial time. Then there exists a p.p.t. algorithm D and a positive polynomial p(⋅) such that for infinitely many n,

(1)

For α a length-n string, let p(α)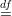Pr[D(α,1ⁿ) = 1]. Then

(2)

(3)

Plugging (2) and (3) into (1) gives

The converse to theorem 1 does not hold.

Proof: We construct the ensemble X = {X_n}_nℕ by choosing for each n a set S_n ⊆{0,1}ⁿ of cardinality N = 2^n∕2 and letting X_n be the uniformly distributed on S_n. Thus, Pr[X_n = α] = 1∕N for α S_n, and Pr[X_n = α] = 0 for α ⁄ S_n.

The fact that X, U are not statistically close is immediate from the above. Using the facts that 2ⁿ = N² and |S_n| = N, and |S_n| = N² - N, we get

The proof in the textbook supplies the low-level details needed to establish this theorem, but it is a little unclear about the construction itself, particularly about how the set S_n is chosen.

We wish to choose a set S_n for which the corresponding distribution X_n is indistinguishable from U_n by every polynomial size circuit C. We do this by diagonalizing over all circuits of size 2^n∕8. We start with all size 2^N subsets of {0,1}ⁿ as candidates for S_n. For each such circuit C, we discard from consideration all candidates on which C is too successful at distinguishing the corresponding ensemble from uniform. By a counting argument, we show that not very many candidates get thrown out at each stage—so few in fact that there are still candidates left after all of the size 2^n∕8 circuits have been considered. We choose any remaining candidate for S_n and conclude that no size 2^n∕8 circuit is very successful at distinguishing X_n from U_n.

More precisely, here’s how to determine which candidates to discard. First, consider an n-input circuit C with at most 2^n∕8 gates. Let p_C be C’s expected output on uniformly chosen inputs. Then C(x) = 1 for a p_C fraction of all length n strings, and C(x) = 0 for the remainder.

Let 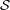_n = {S ⊆{0,1}ⁿ∣|S| = 2^N}. This is the initial family of candidate sets. Let f_C : 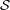_n →{0,1}, where

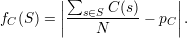
Thus, f_C(S) is the amount that the average value of C(s) taken over strings s S differs from the average value of C(u) taken over all length-n strings u. By the law of large numbers, we would expect f_C(S) to be very small with high probability for randomly chosen S . Call a set S bad for C if f_C(S) ≥ 2^-n∕8. Using the Chernoff bound, one shows that the fraction of sets S _n that are bad for C is less than 2^-2n∕4 . (Details are in the book.)

Next, one argues that there are at most 2^2n∕4 circuits of size 2^n∕8. (This is by a counting argument. Details are not in the book and should be verified.) From this, it follows that there is at least one set S_{n n} which is not bad for any such circuit. Fix such a set.

Now, let X_n be uniformly distributed over S_n. Observe that the following three quantities are all the same: the expected value of C(X_n), Pr[C(X_n) = 1], and ∑ _sSC(s)∕N. Hence, for all circuits C of size at most 2^n∕8, we have |Pr[C(X_n) = 1] -Pr[C(U_n) = 1]| = f_C(S_n) < 2^-n∕8, which grows more slowly than 1∕p(n) for any polynomial p(⋅). We conclude that the probabilistic ensembles U and X are indistinguishable by polynomial-size circuits, which also implies polynomial-time indistinguishability by probabilistic polynomial-time Turing machines. __

We remark that a consequence of theorem 2 is that the set S_n on which X_n has non-zero probability mass cannot be recognized in polynomial time. Assume to the contrary that it could be recognized by some polynomial time algorithm A, that is, A(x) = 1 if x S_n and A(x) = 0 otherwise.. Then A itself would distinguish X_n from U_n. Clearly, Pr[A(X_n) = 1] = 1 but Pr[A(U_n) = 1] = |S_n|∕2ⁿ. Since |S_n| = 2^n∕2, these two probabilities differ by 1 -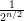 which is greater than 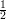for all sufficiently large n. (Note that the constant 2 is also a polynomial!)

28 Indistinguishability by Repeated Sampling

The definition of polynomial time indistinguishability given in section 26 gives the distinguishing algorithm D a single random sample from either X or Y and compare the two probabilities of it outputting a 1. We can generalize that definition in a straightforward way by providing D with multiple samples, as long as the number of samples is itself bounded by a polynomial m(n). If the difference in output probabilities in this case is a negligible function, we say that X, Y are indistinguishable by polynomial-time sampling. See Definition 3.2.4 of the textbook for details

Giving D multiple samples allows for new possible distinguishing algorithms. For example, consider the algorithm Eq(x,y) that outputs 1 if x = y and 0 otherwise. Eq able to distinguish the ensemble X of Theorem 2 from U. Let’s analyze the probabilities.

since no matter what value X_n¹ assumes, there is a 1∕N chance that the second (independent) sample is equal to it. (Recall that N = 2^n∕2.) On the other hand,

The difference of these two probabilities is clearly non-negligible.

However, it turns out that multiple samples are only helpful in cases such as this where at least one of the distributions cannot be constructed in polynomial time, as we shall see.

28.1 Efficiently constructible ensembles

We say that an ensemble X = {X_n}_nℕ is polynomial-time constructible if there exists a polynomial-time probabilistic algorithm S such that the output distribution S(1ⁿ) and X_n are identically distributed.

28.2 Multiple samples don’t help with constructible ensembles

Proof: The proof is an example of the hybrid technique, also sometimes called an interpolation proof. Here’s the outline of it.

Assume X, Y are distinguishable by D using m = m(n) samples. Let X_n⁽¹⁾,…,X_n^(m) be independent random variables identically distributed to X_n and similarly for Y . Let

and let

By assumption, D can distinguish X, Y , so the difference δ(n) = |p(x) = p(y)| is non-negligible.

We now construct a sequence of hybrid m-tuples of random variables for k = 0,…,m:

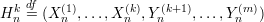
Clearly, H_n⁰ consists of all Y ’s, and H_n^m consists of all X’s. Hence, D distinguishes between H_n⁰ and H_n^m with probability δ(n).

Now let δ_k(n) be the absolute value of the difference in D’s probability of outputting a 1 given H_n^k and H_n^k+1. It is easily seen that ∑ _k=0^m-1δ_k(n) ≥ δ(n); hence, for some particular value of k = k₀,

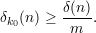
We now describe a single-sample distinguisher D′. On input α, it first chooses a random number k from {0,…,m-1} Next, it generates k independent random numbers x₁,…,x_k distributed according to X_n and m - k - 1 random numbers y_k+2,…,y_m distributed according to Y _n. It can do this by the assumption that X and Y are polynomial-time constructible. It then constructs h = (x₁,…,x_k,α,y_k+2,…,y_m), runs D(h), and outputs the result.

Note that h is distributed according to H_n^k if α was chosen according to Y , and h is distributed according to H_n^k+1 if α was chosen according to X. Thus, the probability that D′ outputs 1 given a sample from X or a sample from Y is at least 1∕m, the probability that D′ chooses k = k₀, times δ_k0(n). Hence, D′ distinguishes with probability difference at least δ(n)∕m², which contradicts the assumption that X, Y are indistinguishable in polynomial time. __