YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 461b: Foundations of Cryptography | Notes 13 (rev. 1) |
| Professor M. J. Fischer | | February 24, 2009 |
|
|
|
| |
32 Review of Lecture 12
Lecture 12 covered several technical proofs fairly quickly. In this lecture, we reviewed the three theorems
from last time and focused on the key ideas that made the proofs work. (The complete proofs are contained
in the written notes for Lecture 12.)
-
Building G from G1:
- The big idea that makes the hybrid proof work is that the distinguisher D′ is
given as argument either α = G1(Un) or α = Un+1. In either case, it splits α into two parts
τ ⋅α′ and constructs the string w = τ ⋅G(α′). If α = G1(Un), then w = τ ⋅G(α′) = G(Un).
If α = Un, then w = U1 ⋅ G(Un). Hence, the difference is simply whether w starts directly
with the bits from G(Un) or whether it starts with a random bit τ followed by G(Un). This
fits in with the construction of the hybrids, so when w is prefixed with a random β of length-k
and truncated to total length p(n), the resulting hybrid is either Hnk or Hnk+1.
-
Pseudorandom ⇐ Unpredictable:
- Here, the hybrids are strings with k bits from the
pseudorandom generator followed by n - k random bits. Assume D is a distinguisher for
the pseudorandom strings. The next-bit predictor A that we construct generates a hybrid for a
randomly-chosen k and then calls the distinguisher D on it. A outputs the first of the n - k
random bits if the distinguisher answers 1, and it outputs the complement otherwise. This
works since D was assumed to be more likely to output 1 on pseudorandom strings than on
truly random ones.
-
Pseudorandom implies strongly one-way
- Given a pseudorandom function G(s) with expansion
factor 2n, the proof constructs the function f(x,y) = G(x) and proceeds to derive a
contradiction to the assumption that f is not strongly one-way. While f is attractive because
it is length-preserving, it seems that the proof goes through just fine for G itself. Assume
G were not strongly one-way, and let A be an algorithm that inverts it with non-negligible
success probability. Then here’s how to distinguish G(s) from U2n. On input α, use A to find
s′ such that G(s′) = α. If such an s′ is found, output 1; else output 0. If the input is α = G(s),
the distinguisher will output 1 with probability the same as A’s success probability, which is
at least
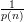 for some polynomial p(⋅). If the input is α = U2n, then the distinguisher will
output 0 whenever U2n is not in the range of G(s) (as s ranges over length-n strings). The
size of the range is 2n but the number of choices for α is 22n, so the probability of giving
output 1 in this case is at most 2n∕22n = 1∕2n. Hence, the difference in probabilities is at
least
for some polynomial p(⋅). If the input is α = U2n, then the distinguisher will
output 0 whenever U2n is not in the range of G(s) (as s ranges over length-n strings). The
size of the range is 2n but the number of choices for α is 22n, so the probability of giving
output 1 in this case is at most 2n∕22n = 1∕2n. Hence, the difference in probabilities is at
least 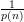 -
-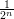 >
> 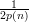 , contradicting the assumption that G is pseudorandom.
, contradicting the assumption that G is pseudorandom.
33 Pseudorandom Generator from Strongly One-Way Permutation
The construction of a pseudorandom generator from an arbitrary strongly one-way function is complicated
and not included in the textbook. However, if strongly one-way permutations exist, then it is
straightforward to construct a pseudorandom generator.
Theorem 1 Let f be a length-preserving 1-1 strongly one-way function and b a hard core for f.
Then
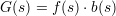
is a pseudorandom generator.
Proof: Assume G is not pseudorandom. Then there exists a bit predictor A with significant
advantage. Let α = G(s), where s = Un. Because f is 1-1, f(Un) is uniformly distributed on
length-n strings, so A can’t predict any of the first n bits of α with any advantage. Since A does
have an advantage overall, then it must have an advantage at predicting bit n+1. But this means that
A is able to get an advantage at predicting b(s) after having read f(s), contradicting the assumption
that b(s) is a hard core for f. __
Theorem 1 gives an easy and efficient method for constructing a polynomial-expansion pseudorandom
number generator given a strongly one-way permutation f with a hard core predicate b. Namely, on initial
seed s, do the following:
34 Pseudorandom Functions
An ℓ-bit function ensemble is a sequence F = {Fn}n ℕ of random variables such that Fn assumes values
in the set of functions mapping ℓ(n)-bit-long strings to ℓ(n)-bit-long strings. The uniform ℓ-bit function
ensemble, H = {Hn}n
ℕ of random variables such that Fn assumes values
in the set of functions mapping ℓ(n)-bit-long strings to ℓ(n)-bit-long strings. The uniform ℓ-bit function
ensemble, H = {Hn}n ℕ, has Hn uniformly distributed over the set of all functions mapping
{0,1}ℓ(n) →{0,1}ℓ(n).
ℕ, has Hn uniformly distributed over the set of all functions mapping
{0,1}ℓ(n) →{0,1}ℓ(n).
Definition: An ℓ-bit function ensemble F is pseudorandom if, for every probabilistic
polynomial-time oracle machine M, every positive polynomial p(⋅), and all sufficiently large n,
![Fn n Hn n -1--
|P r[M (1 ) = 1]- P r[M (1 ) = 1]| < p(n).](ln135x.png)
Definition: An ℓ-bit function ensemble F is efficiently computable iff there exist polynomial-time
algorithms I, V such that
- ϕ(I(1n)) and Fn are identically distributed, where ϕ maps strings to functions. (Think of the
strings as somehow describing functions, and ϕ(i) is the function that the string i describes.)
- V (i,x) = fi(x) for every i in the range of I(1n) and x
 {0,1}ℓ(n), where fi = ϕ(i) is the
function described by i.
{0,1}ℓ(n), where fi = ϕ(i) is the
function described by i.
In the next lecture, we will show how to construct an efficiently computable ℓ-bit pseudorandom
function ensemble, starting from a pseudorandom generator G with expansion factor 2n.
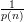 for some polynomial p(⋅). If the input is α = U2n, then the distinguisher will
output 0 whenever U2n is not in the range of G(s) (as s ranges over length-n strings). The
size of the range is 2n but the number of choices for α is 22n, so the probability of giving
output 1 in this case is at most 2n∕22n = 1∕2n. Hence, the difference in probabilities is at
least
for some polynomial p(⋅). If the input is α = U2n, then the distinguisher will
output 0 whenever U2n is not in the range of G(s) (as s ranges over length-n strings). The
size of the range is 2n but the number of choices for α is 22n, so the probability of giving
output 1 in this case is at most 2n∕22n = 1∕2n. Hence, the difference in probabilities is at
least 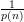 -
-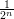 >
> 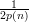 , contradicting the assumption that G is pseudorandom.
, contradicting the assumption that G is pseudorandom.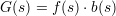

![Fn n Hn n -1--
|P r[M (1 ) = 1]- P r[M (1 ) = 1]| < p(n).](ln135x.png)
 {
{