43 Zero Knowledge Interactive Proof Systems

Zero knowledge is a property of the prover P in an interactive proof system (P,V ) for a language L. Intuitively, it says that whatever an arbitrary polynomial-time interactive Turing machine V ^* could compute while interacting with P on input x L could be computed by an ordinary (non-interactive) probabilistic polynomial-time Turing machine M^*. Thus, V ^* is not able to compute anything with P ’s help that could not already have been computed in polynomial time without P ’s help.

43.1 Zero knowlege based on output distributions

As with the notion of interactive proof system, there are a variety of different notions of zero knowledge. We begin with the strongest (and least useful).

Definition: Let (P,V ) be an interactive proof system for a language L. P is said to be strongly perfect zero knowledge if for all polynomial-time interactive Turing machines V ^* there exists a probabilistic polynomial-time (ordinary) algorithm M^* (called the simulator) such that for all x L, the random variables ⟨P,V ^*⟩(x) and M^*(x) are identically distributed.

This definition is too strong to capture the intuition, for it requires the simulator to be both strictly polynomial time and also generate exactly the same output distribution as does the interactive pair ⟨P,V ^*⟩ on the same input. In most cases, a machine that runs in strictly polynomial time is equally useful as one that runs in expected polynomial time. Indeed, the latter can be converted into the former by adding a “clock” that shuts off the machine after it has taken q(|x|) steps for a suitably large polynomial q. However, the modified machine now has an exponentially small probability of failure, so its output distribution is not exactly identical to that of the expected time machine, only almost identical.

We could get around this problem by weaking the requirement that the distributions be identical (and indeed one way of doing so leads to the notion of statistical zero knowledge). However, we can still preserve the notion of perfection with the following.

Definition: Let (P,V ) be an interactive proof system for a language L. P is said to be perfect zero knowledge if for all polynomial-time interactive Turing machines V ^* there exists a probabilistic polynomial-time (ordinary) algorithm M^* (called the simulator) such that for all x L, the following two conditions hold:

1. Pr[M^*(x) = ⊥] ≤ 1∕2, where ⊥ is a special symbol not in {0,1}.
2. The random variables ⟨P,V ^*⟩(x) and m^*(x) are identically distributed, where m^*(x) is M^*(x) conditioned on M^*(x)≠⊥. That is, for all α {0,1}, Pr[m^*(x) = α] = Pr[M^*(x) = α∣M^*(x)≠⊥].

With perfect zero knowledge, we allow the simulator to fail, but on those runs where it succeeds, it must generate the correct output distribution. It’s easy to see that repeating the simulator until it succeeds yields an expected polynomial-time simulation with the exactly correct output distribution, and repeating it a polynomial number of times yields a strictly polynomial-time simulation with an exponentially small error probability.

We next give a weaker version of zero knowledge that still captures the intuition of the prover not leaking information that will materially aid an adversary. Definition: Let (P,V ) be an interactive proof system for a language L. P is said to be computational zero knowledge if for all polynomial-time interactive Turing machines V ^* there exists a probabilistic polynomial-time (ordinary) algorithm M^* (called the simulator) such that for all x L, the random variables ⟨P,V ^*⟩(x) and M^*(x) are computationally indistinguishable.

The only difference between this definition and the original strong perfect zero knowledge is the relaxation of ‘identically distributed” requirement to the weaker “computationally indistinguishable” requirement. We note that allowing M^* to output ⊥ up to half the time as we do with perfect zero knowledge does not change the power of computational zero knowledge, so we will feel free to do so when constructing the simulator to establish computational zero knowledge.

43.2 Zero knowledge based on views

One can also define various notions of zero knowledge, not in terms of V ^*’s output, but in terms of the transcript of the interaction between P and V ^*. Let viewP V^*(x) be the random variable describing the content of V ^*’s random tape and the messages V ^* receives during its joint computation with P . We then say that (P,V ) is computational zero knowledge if the ensembles of random variables

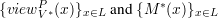
are computationally indistinguishable. In this definition, the simulator M^* is different than before. Here, M^*(x) must output the view of M interacting with V ^*, not just V ^*’s output.

Outputting the view is at least as strong a requirement as mimicking V ^*’s output, for if we have a machine M^*(x) that outputs the view (with the correct distribution), then we can easily construct a machine M^*′(x) that produces V ^*’s output. Namely, M^*′(x) first runs M^*(x) to obtain the view. Then it simulates V ^*(x), referring to the view to initialize V ^*’s random tape and to supply the incoming messages to V ^*(x) as needed.

44 A Zero Knowledge Interactive Proof for Graph Isomorphism

The graph isomorphism language GI is the set of all pairs of graphs (G₁,G₂) such that G₁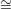G₂.

Here is a high-level description of an interactive proof system (P,V ) for GI. Let x = (G₁,G₂) GI. On input x, the protocol works as follows:

1. P generates a random isomorphic copy H of G₂ and sends H to V .¹
2. V picks σ {0,1} uniformly at random and sends σ to P .
3. P responds with an isomorphism ψ from G_σ to H.²
4. V accepts iff ψ(G_σ) = H.

We remark that P , as described above, is not fully defined. In particular, what does P do if it receives a value σ ⁄{1,2}? Since this never occurs when P interacts with V , it doesn’t matter to the correctness of (P,V ) as an interactive proof system for GI, but it will become important in establishing zero knowledge. We therefore complete the definition of P by specifying that P shall treat any value of σ≠2 as if it were 1, that is, it returns an isomorphism from G₁ to H in step 3 whenever σ≠2.

44.1 (P,V ) is an interactive proof system for GI

If indeed G₁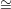G₂, it is easy to see that V always accepts. On the other hand, if G₁ ⁄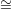G₂ and H is the graph returned by an arbitrary prover B in step 1, then it is impossible for B in step 3 to successfully answer both of V ’s possible queries, for there do not exist two isomorphisms ψ₁ and ψ₂ such that ψ₁(G₁) = H and ψ₂(G₂) = H. If there did, then it would follow that G₁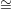H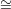G₂, contradicting the assuming that G₁ ⁄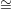G₂. Since V chooses σ uniformly and independently from {1,2}, it will, with probability ≥ 1∕2, choose σ such that G_σ ⁄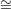H, in which case it will reject whatever ψ is returned by B in step 3.

44.2 P is perfect zero knowledge over GI

Let q(⋅) be a polynomial and let V ^* be an interactive Turing machine with time complexity q. To show that P is perfect zero knowledge, we construct a view-based simulator M^* for (P,V ^*). For simplicity, we will assume that V ^* never halts prematurely, that is, it never halts before producing its outgoing message σ and ceding control back to the prover.

We represent a view by a 4-tuple (x,r,H,ψ), where x is the common input, r is V ^*’s random tape, H is P ’s first message, and ψ is its second message. The view completely determines the computation by V ^* since it specifies its input, random choices, and received messages. The job of M^*(x) is to produce views with the same distribution as occurs when P interacts with V ^* on common input x.

Given input x = (G₁,G₂) GI, M^*(x) proceeds as follows:

1. Choose r uniformly in {0,1}^q(|x|).
2. Choose τ uniformly in {0,1}. Let W_τ be the vertex set of graph G_τ. Choose ψ uniformly from the permutations on W_τ and let H = ψ(G_τ).³
3. Put x, r, and H on V ^*’s input tape, random tape, and incoming communication tape, respectively. Run V ^* until it produces a message on its outgoing communication tape and suspends by writing to the switch tape.⁴ Let σ′ be V ^*’s outgoing message. Let σ = σ′ if σ′ {1,2}, otherwise let σ = 1.⁵
4. If σ = τ, output (x,r,H,ψ). Otherwise, output ⊥.

We remark that M^* is required to be polynomial time, whereas P has no such restriction. Therefore, the simulator cannot create the prover’s messages H and ψ in the same way that P does. Rather, it uses τ to guess what σ will be in step 2 of the protocol, generates a random isomorphism ψ, and chooses H = ψ(G_τ). If it guesses correctly, then it can answer V ’s query σ by responding with ψ. If not, then it fails and outputs ⊥.

We must show that M^* satisfies the conditions for the simulator, that is, it outputs ⊥ with probability at most 1∕2, and conditioned on not outputting ⊥, its output has the same distribution as viewP V ^*(x).

A key point in establishing that M^*(x) outputs the correct probability distribution on views is the observation that V ^* has no information about the simulator’s choice of τ when it computes its message σ. Because it does have some information from the simulator at that time (namely, H), this is a non-trivial concern that perhaps H somehow leaks information about τ. In fact, H = ψ(G_τ) does seem to depend on τ, reinforcing our concern.

As with the graph non-isomorphism protocol in section 41, the answer to the concern is a Bayes’ theorem analysis to show that τ is equally likely to be 1 or 2, even given the value H of the random variable ψ(G_τ). That is,

The proof is similar to what was written out in section 41 and is omitted here. Further details can be found in the textbook under Claim 4.3.9.1.

We now complete the proof that P is zero knowledge for GI.

On any run, M^*(x) = ⊥ in case σ≠τ in step 4. Because σ,τ {1,2}, σ is independent of τ, and τ is equally likely to be 1 or 2 given H, it follows that σ≠τ with probability exactly 1∕2. Hence, Pr[M^*(x) = ⊥] = 1∕2.

We must now show that M^*(x) outputs views with the right probability distribution. Let m^*(x) be M^*(x) conditioned on M^*(x)≠⊥. Let ν(x,r) be the random variable describing the last two elements of viewP V ^*(x), conditioned on the second element being r. (The first element, x, is fixed and not chosen at random.) Similarly, let μ(x,r) be the random variable describing the last two elements of m^*(x), conditioned on the second element being r. It remains to show that ν(x,r) and μ(x,r) are identically distributed for all x and r.

Let v^*(x,r,H) be the message σ sent by V ^* on common input x, random tape r, and incoming message H. v^*(x,r,H) is completely determined by its inputs, so v^* is an ordinary (not random) function.

Claim 1 Random variables ν(x,r) and μ(x,r) are both uniformly distributed over the set

From the claim and the fact that r is uniformly distributed in both the original protocol and in the simulator, it follows that viewP V^*(x) = (x,R) ⋅ ν(x,R) and m^*(x) = (x,R) ⋅ μ(x,R) are identically distributed, where R is a uniform random variable over {0,1}^q(|x|), establishing that P is perfect zero knowledge over GI.

It remains to prove claim 1. Proof: In viewP V^*(x), H is uniformly distributed over graphs isomorphic to G₂. In m^*(x), H is a uniform mixture of graphs isomorphic to G₁ and graphs isomorphic to G₂. Since G₁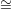G₂, these two distributions are identical.

For each H, there is exactly one isomorphism ψ such that H = ψ(G_v^*(x,r,H)) and hence exactly one pair (H,ψ) C_x,r. Since we have already argued that the H-component of ν(x,r) and μ(x,r) is uniformly distributed, it remains only to show that ν(x,r) and μ(x,r) are both contained in C_x,r.

Suppose ν(x,r) = (H,ψ). Then (x,r,H,ψ) is contained in viewP V^*(x). Since ψ is the second value sent by P , it satisfies ψ(G_σ) = H, where σ = v^*(x,r,H) is the first value sent by V ^*. Hence, ν(x,r) C_x,r.

Suppose μ(x,r) = (H,ψ). Then (x,r,H,ψ) is output by M^*(x). Under the conditioning assumption, we know that σ = τ in step 4 of the code for M^*, so ψ(G_τ) = ψ(G_σ) = H, where again, σ = v^*(x,r,H) is the first value sent by V ^*. Hence, μ(x,r) C_x,r. __

A slightly more careful and complete proof may be found on page 212 of the textbook.