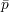
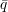 , and |
, and |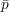 |≈|
|≈|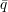 |≈
|≈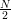 . A protocol that intuitively works is shown in
Figure 53.1.1
. A protocol that intuitively works is shown in
Figure 53.1.1
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 461b: Foundations of Cryptography | Notes 21 (rev. 1) | |
| Professor M. J. Fischer | April 9, 2009 | |
Lecture Notes 21
The Millionaire’s Problem, introduced by Andy Yao in 1982, began the study of privacy-preserving multiparty computation.
Alice and Bob want to know who is the richer without revealing how much they are actually worth. Alice is worth I million dollars; Bob is worth J million dollars. They want to determine whether or not I ≥ J, but at the end of the protocol, neither should have learned any more about the other person’s wealth than is implied by the truth value of the predicate I ≥ J.
For simplicity, we assume that I and J are both in the set {1,2,…,10}. Let N be a
security parameter, and assume that Alice has public and private RSA keys (e,n) and (d,n),
respectively, where n = 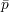
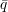 , and |
, and |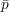 |≈|
|≈|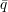 |≈
|≈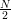 . A protocol that intuitively works is shown in
Figure 53.1.1
. A protocol that intuitively works is shown in
Figure 53.1.1
In step 1, Bob sends Alice a random-looking number m. The number m + J - 1 is the encryption of Bob’s secret x. Alice decrypts the numbers m,m + 1,…,m + 9 to get corresponding Y 1,…,Y 10. The number Y J is Bob’s secret x, but Alice doesn’t know which it is since all of the Y i’s “look” random. She then reduces them all mod a random prime p, resulting in Z1,…,Z10. Note that ZJ = x mod p and the other Zi’s look random. Finally, she adds 1 (modp) to each of the numbers Zi for which i is greater than her own wealth I. If she adds 1 to ZJ, this means that J > I; if not J ≤ I. Bob can tell with is the case from the numbers that Alice sends him in step 2. Namely, if WJ ≡ x (mod p), this means that 1 was not added, so I ≥ J. Otherwise, I < J.
Clearly, all that Alice learns from Bob is a set of random-looking numbers m,…,m + 9, one of which corresponds to Bob’s wealth J, but she has no way of telling which, since any number in Z* n is the RSA encryption of some plaintext message. Bob on the other hand receives p and W1,…,W10 from Alice in step 2. However, he does not know any Zi for i≠J since he cannot the corresponding numbers m + i- 1. He also cannot recover Y i from Wi because of the information loss implicit in the “mod p” operation. Thus, he also learns nothing about Alice’s wealth I except for the value of the predicate I ≥ J.
We remark that this protocol works only in the semi-honest model in which both Alice and Bob follow their protocol, but both will try to infer whatever they can about the other’s secrets after the fact.
How to define security in a multiparty protocol is far from obvious. For example, in the millionaire’s problem, there is no way to prevent either Alice or Bob from lying about their wealth, nor is it possible to prevent either of them voluntarily giving up secrecy by broadcasting their wealth. Thus, we can’t hope to find a protocol that will prevent all kinds of cheating. What we do instead is to compare a given “real” protocol with a corresponding very simple “ideal” protocol involving a trusted party. The idea is that the real protocol should simulate the ideal protocol, much the same as the simulator of a zero knowledge proof system simulates the real interaction between prover and verifier. The real protocol is deemed to be secure if any bad things that can happen in the real protocol are also possible in the ideal protocol.
For example, the ideal protocol for the millionaire’s problem has just two steps: In step 1, Alice and Bob send their secrets I and J, respectively, to the trusted party across a private, secure channel. In step 2, the trusted party computes the value of the predicate I ≥ J and sends the result back to both Alice and Bob. The goal of the real protocol is that Alice and Bob don’t learn any more than they could learn in the ideal protocol.
But what is it that an ideal multiparty protocol computes? Suppose there are m parties to the protocol, P1,…,Pm. Each Pi has a private input xi and receives a private output yi. We say that F is a (multi-party) functionality if F is a random process that maps m inputs to m outputs. As a special case, we say that F is deterministic if the m outputs are uniquely determined by the m inputs.
The millionaire’s problem can be expressed simply as the problem of securely computing the (deterministic) functionality F(I,J) = ((I ≥ J),(I ≥ J)) in the semi-honest model.
There is no simple choice of the “right” security model for multiparty computations. As with other aspects of cryptography, different kinds of threats are deemed significant in different situations. We list below some of the parameters that are important in the literature on secure multiparty computation.
OT1k, 1-out-of-k oblivious transfer, is the functionality
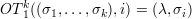
where σ1,…,σk  {0,1} and i
{0,1} and i  {1,…,k}. Here, the first party (Alice) has k secret bits σ1,…,σk. Bob has
a secret index i. At the end of the protocol, Bob learns only σi and Alice learns nothing (λ). In particular,
Alice does not know which of her bits was learned by Bob, and Bob does not learn σj for any
j≠i.
{1,…,k}. Here, the first party (Alice) has k secret bits σ1,…,σk. Bob has
a secret index i. At the end of the protocol, Bob learns only σi and Alice learns nothing (λ). In particular,
Alice does not know which of her bits was learned by Bob, and Bob does not learn σj for any
j≠i.
Oblivious transfer is central to many of the constructions for secure multiparty computation. We give a
protocol for OT1k in the semi-honest model. Our construction assumes an enhanced trapdoor permutation
{fα : Dα → Dα}α I. (See appendix of Volume 2 for technical information on exactly what it means to be
enhanced.) Roughly speaking, given a security parameter 1n and a random string r, there is an algorithm
G(1n,r) that returns a pair (α,t), where α is the index of a trapdoor permutation fα and t is a trapdoor.
(Think of RSA key generation, where we randomly generate a public and private key pair.)
Moreover, there is a feasible algorithm for computing fα(x) given α and x, and there is a feasible
algorithm for computing fα-1(y) given t and y. We also assume that b is a hard-core predicate for
fα.
I. (See appendix of Volume 2 for technical information on exactly what it means to be
enhanced.) Roughly speaking, given a security parameter 1n and a random string r, there is an algorithm
G(1n,r) that returns a pair (α,t), where α is the index of a trapdoor permutation fα and t is a trapdoor.
(Think of RSA key generation, where we randomly generate a public and private key pair.)
Moreover, there is a feasible algorithm for computing fα(x) given α and x, and there is a feasible
algorithm for computing fα-1(y) given t and y. We also assume that b is a hard-core predicate for
fα.
Our construction is shown in Figure 57.1. The idea behind the protocol is that Bob sends Alice a k-tuple (y1,…,yk) of numbers. All yj are random except for yi; yi is the encryption of a random number xi. Alice decrypts them all to get z1,…,zk, XOR’s the associated hard-core predicate b(zj) with each of her secrets σj, and sends the encrypted secrets (c1,…,ck) to Bob. Because yi is the encryption of xi, then zi = xi, so Bob is able to compute b(zi) and decrypt ci to obtain σi. He doesn’t learn the other secrets since for j≠i, he knows only xj = fα(zi). He cannot predict b(zi) given xj with more than an negligible advantage since b is hard-core for fα.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
Theorem 1 Suppose {fα : Dα → Dα}α I is a collection of enhanced trapdoor permutations and
b is a hard-core predicate for them. Then the protocol of Figure 57.1 privately computes OT1k in
the semi-honest model.
I is a collection of enhanced trapdoor permutations and
b is a hard-core predicate for them. Then the protocol of Figure 57.1 privately computes OT1k in
the semi-honest model.