YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE

	CPSC 467a: Cryptography and Computer Security	Handout #10
Yinghua Wu		October 22, 2006

Solutions to Problem Set 2

Problem 2: Affine Cipher (2.13.4)

From the chosen plaintext attack, we have

{ 0 α+ β ≡ 14 (mod 26) 7 α+ β ≡ 13 (mod 26)

We get β ≡ 14 (mod 26) immediately, and then obtain 7α ≡-1 (mod 26). Using Extended Euclidean Algorithm, we can easily get 7^-1 ≡-11 (mod 26), so α ≡ 11 (mod 26). Thus, the decryption function is x11x + 14 (mod 26).

Problem 3: Vigenere Cipher (2.13.10)

You can make left shifting or right shifting or left wrapping shifting or right wrapping shifting to calculate the number of coincidences and come to the result that the key length is probably 2.

From the letter frequency, we have A₀ = {0.1,0.9}. We study the odd positions of the ciphertext and get W = {0.2,0.8}. Obviously, W ⋅A₀ > W ⋅A₁, so the first key is 0 = a. Similarly, we obtain the second key is 1 = b. And finally we decrypt the ciphertext to get bbbbbbabbb.

Problem 4: Hill Cipher (2.13.15)

From the chosen plaintext attack, we have

( ) ( ) ( ) 1 0 a b 7 2 25 25 c d ≡ 6 19 (mod 26).

Since

( ) 1 0 det 25 25 ≡ 25 ≡ - 1 (mod 26),

and gcd(-1,26) = 1, we have (-1)^-1 ≡-1 (mod 26). So we obtain the inverse matrix

( ) -1 ( ) 1 0 1 0 25 25 = - 1 - 1 .

Thus

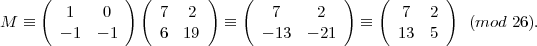
( ) ( ) ( ) ( ) M ≡ 1 0 7 2 ≡ 7 2 ≡ 7 2 (mod 26). - 1 - 1 6 19 - 13 - 21 13 5

Problem 5: LFSR Machine (2.13.21)

Pick the sequences with 0 to make the answer evident.

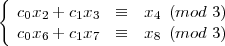
{ c0x2 + c1x3 ≡ x4 (mod 3) c0x6 + c1x7 ≡ x8 (mod 3)

We immediately get c₀ ≡ 2 (mod 3) and c₁ ≡ 1 (mod 3).

Problem 6: Chaining Modes

ECB: : All other ciphertext blocks except the lost one can be decrypted correctly.
CBC: : The lost ciphertext block and the sequential one can’t be correctly decrypted, while all other blocks can be.
CFB: : The lost ciphertext block and the sequential one can’t be correctly decrypted, while all other blocks can be.
OFB: : All other ciphertext blocks except the lost one can be decrypted correctly.
PCBC: : The lost ciphertext block and all the sequential ones can’t be correctly decrypted.

Problem 7: Birthday Paradox Calculation

Since p_m = 1 - prob[two subsets have an empty intersection], we compute the item on the right side first. There are totally (100 m ) (100 m ) choices to draw two random subsets of size m, and there are ( 100 m) (100-m m ) choices to draw two non-overlapped random subsets of the same size. We obtain that

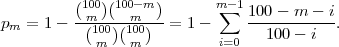
( )( ) -1m00--100-m-m-- m∑-1 100--m----i pm = 1 - (100)(100) = 1 - 100 - i . m m i=0

Use a program to try m = 1 ⋅⋅⋅ 20, and get m = 9 for p_m ≥ 1∕2 and m = 12 for p_m ≥ 3∕4.

Problem 8: Meet-in-the-Middle Attack

(a) We are guaranteed of finding at least one match, since if (k₁,k₂) is the real key pair used in the double encryption, then E_k₁(m) = D_k₂(c).

(b) If there is only one match, then we have found the key pair and broken the system. If there are several matches, we know that the key pair is one of the matching pairs. This set is likely to be much much smaller than the original key space, so they can each be tried on additional plaintext-ciphertext pairs to find which ones work.

(c) Considering a double Caesar cipher, no matter what keys you are choosing, X_m and X_c will generate the all 26 letters of the whole space. So X_m ⋂ X_c = 26 ≥ 2.