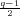 ≡-1 (mod q). And because y is not a square mod q, according to Euler Criterion, y
≡-1 (mod q). And because y is not a square mod q, according to Euler Criterion, y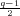 ⁄≡-1
(mod q). But yq-1 ≡ 1 (mod q) and 1’s two square roots are ±1, so y
⁄≡-1
(mod q). But yq-1 ≡ 1 (mod q) and 1’s two square roots are ±1, so y ≡-1 (mod q). Thus we
have
≡-1 (mod q). Thus we
have
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Handout #19 (rev. 2) | |
| Yinghua Wu | December 17, 2006 | |
Solutions to Problem Set 7
(a) Assume y is a square both mod p and mod q, i.e. bp2 ≡ y (mod p) and bq2 ≡ y (mod q). Since
gcd(p,q) = 1, according to Chinese Remainder Theorem, there exists exactly one solution b so that b ≡ bp
(mod p) and b ≡ bq (mod q). So b2 ≡ y (mod p) and b2 ≡ y (mod q). Thus p∣(b2 -y) and q∣(b2 -y),
which means pq∣(b2 -y). So we conclude that b2 ≡ y (mod n), which contradicts the fact that y doesn’t
have a square root mod n. The same proof applies to -y. So neither y nor -y can be a square both mod p
and mod q.
(b) Since q ≡ 3 (mod 4), then q = 4m + 3 and (q - 1)∕2 = 2m + 1 is odd, where m is an integer. So
(-1)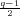 ≡-1 (mod q). And because y is not a square mod q, according to Euler Criterion, y
≡-1 (mod q). And because y is not a square mod q, according to Euler Criterion, y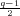 ⁄≡-1
(mod q). But yq-1 ≡ 1 (mod q) and 1’s two square roots are ±1, so y
⁄≡-1
(mod q). But yq-1 ≡ 1 (mod q) and 1’s two square roots are ±1, so y ≡-1 (mod q). Thus we
have
≡-1 (mod q). Thus we
have
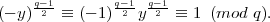
Again according to Euler Criterion, we know that -y is a square mod q.
(c) The result immediately follows from (a) and (b). To be specific, from (a), neither y and -y can be a square both mod p and mod q. We discuss it in two cases:
From the above description, we know that y can’t be a quadratic non-residue of both p and q. So the above
description is sufficent and the proposition is proven.
(d)
Problem 30: Indistinguishability
Since Un is the uniform distribution on binary strings of length n, Un can be regarded as coming from n flips of a fair coin. And the only way we know so far to distinguish two probability distributions is to predict their results and find the difference on their prediction accuracy. So the following solutions are both seeking the proper prediction methods under this knowledge.
(a) J(z) tries to distinguishes U1 from X1 by predicting their outputs, i.e. 1(”heads”) or 0(”tails”). Since U1 comes from a flip of a fair coin, predicting either 1 or 0 provides the same success/failure probability of 1∕2. And for X1 using a biased coin, predicting 1 provides the maximum success probability of 2∕3 while predicting 0 provides the maximum failure probability of 1 - 1∕3 = 2∕3. So J(z) can output 1 either to indicate success prediction or failure prediction, and both generate the same distinguishibility:
![∣Pr[J(U ) = 1]- Pr [J (X ) = 1]∣ = 2∕3- 1∕2 = 1∕6.
1 1](ho195x.png)
And this is the largest value for ε using prediction method for J(z).
(b) When we want to distinguish Un from Xn, we can focus on some specific patterns of strings, or focus on general statistics. Since specific patterns appear with low probability especially when n →∞, we focus on the latter. Consider the number of 1 which appear in the two strings. Assume J(z) will output 1 if the number of 1 is no less than m, in which 0 ≤ m ≤ n, then we have
![n ( )n
Pr[J(Un ) = 1] = ∑ Ci 1-
i=m n 2
n∑ ( )i( )n- i
Pr[J(Xn ) = 1] = Cin 2- 1- .
i=m 3 3](ho196x.png)
![∣∣n ( i )∣∣
∣Pr[J(U ) = 1]- Pr[J(X ) = 1]∣ = ∣∣∑ Ci 2-- 1--∣∣.
n n ∣i=m n 3n 2n ∣](ho197x.png)
We get rid of negative items in the series so as to maximize the above value, i.e.  -
-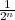 > 0, which
induces m > log 2(3n∕2) ≈ 0.6n. Figure 1 shows that ε almost strictly increases when n increases. And
the minimum value is 1∕6 when n = 1 as in (a).
> 0, which
induces m > log 2(3n∕2) ≈ 0.6n. Figure 1 shows that ε almost strictly increases when n increases. And
the minimum value is 1∕6 when n = 1 as in (a).
Actually, when n →∞, Pr[J(Un) = 1] → 0 while Pr[J(Xn) = 1] → 1. This can be proven using Central Limit Theorem, whose details will be skipped here.