 pmk. This is the
probability of m being generated by the simple process that chooses r letters one at a time according to the
probability distribution (p0,…,p25).
pmk. This is the
probability of m being generated by the simple process that chooses r letters one at a time according to the
probability distribution (p0,…,p25).
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Notes 4 (rev. 1) | |
| Professor M. J. Fischer | September 19, 2006 | |
Lecture Notes 4
In the previous lecture, we discussed what a brute force attack on the Caeser cipher would look like: Decrypt the ciphertext using each of the 26 possible keys, and see which decryption “looks like” a valid message. With English-language messages, this works quite well in practice—generally all of the decryptions but the correct one will be immediately recognized as garbled nonsense. The only sensible-looking decryption is therefore the correct one.
A cryptanalyst might wish to automate the whole process. The question is, how does one write a program to distinguish valid English sentences from gibberish? One could imagine applying all sorts of complicated natural language processing techniques to this task. However, much simpler techniques can be nearly as effective.
One simplification is to consider random messages whose letter frequencies are similar to that of valid
English sentences. That is, for each letter k, let pk be the probability (relative frequency) of that letter in
normal English text. Then a message m = m1m2…mr has probability pm1 ⋅ pm2 pmk. This is the
probability of m being generated by the simple process that chooses r letters one at a time according to the
probability distribution (p0,…,p25).
pmk. This is the
probability of m being generated by the simple process that chooses r letters one at a time according to the
probability distribution (p0,…,p25).
Now, assume that Eve obtains a ciphertext c = Ek(m), where she knows that m was chosen randomly as described above and k is a uniformly distributed Caeser cipher key. Eve easily computes the 26 possible plaintext messages D0(c),...,D25(c), one of which is correct. To choose which, she computes the conditional probability of each message given c, then picks the message with the greatest probability. This guess will not always be correct, but for letter distributions that are not too close to uniform and sufficiently long messages, it works correctly with very high probability.
The Caeser cipher uses only the 26 rotations out of the 26! permutations on the alphabet. The monoalphabetic cipher uses them all. A key k is an arbitrary permutation of the alphabet. Ek(m) replaces each letter a of m by k(a) to yield c. To decrypt, Dk(c) replaces each letter b of c by k-1(b).
The size of the key space is ∣ ∣ = 26! > 274, which is too large for a successful brute force attack.
However, monoalphabetic ciphers can be readily broken using letter frequency analysis, given a long
enough message. Because each occurrence of a letter a in the message is replaced by the same letter k(a),
the most frequently-occurring letter of m will correspond to the most frequently-occurring letter of c.
While Eve might not know what the most frequently-occurring letter of m is, if the message is long enough
and she knows that it is English, then it is quite likely that the most frequently-occurring letter in m is
one of the most frequently-occurring letters in English, i.e., ‘e’ or maybe ‘t’. She can then
assume that the most frequent letter b1 in c is ‘e’, the next most frequent letter b2 is ‘t’, and so
forth. Of course, not all of these guesses will be correct, but the number of likely candidates
for each ciphertext letter is greatly reduced. Moreover, many wrong guesses can be quickly
discarded even without constructing the entire trial key because they lead to unlikely letter
combinations.
∣ = 26! > 274, which is too large for a successful brute force attack.
However, monoalphabetic ciphers can be readily broken using letter frequency analysis, given a long
enough message. Because each occurrence of a letter a in the message is replaced by the same letter k(a),
the most frequently-occurring letter of m will correspond to the most frequently-occurring letter of c.
While Eve might not know what the most frequently-occurring letter of m is, if the message is long enough
and she knows that it is English, then it is quite likely that the most frequently-occurring letter in m is
one of the most frequently-occurring letters in English, i.e., ‘e’ or maybe ‘t’. She can then
assume that the most frequent letter b1 in c is ‘e’, the next most frequent letter b2 is ‘t’, and so
forth. Of course, not all of these guesses will be correct, but the number of likely candidates
for each ciphertext letter is greatly reduced. Moreover, many wrong guesses can be quickly
discarded even without constructing the entire trial key because they lead to unlikely letter
combinations.
A cipher that encrypts two letters at a time is much harder to break than a monoalphabetic cipher since it tends to mask the letter frequencies. The Playfair cipher, popularized by L. Playfair in England circa 1854, is one such example.1 Here, the key is a 5 × 5 matrix of letters. Pairs of plaintext letters are located in the matrix and used to produce a corresponding pair of ciphertext letters.
For example, consider the key matrix that might result from the passphrase, “CRYPTOGRAPHY REQUIRES STRONG KEYS”:
| C | R | Y | P | T |
| O | G | A | H | E |
| Q | U | I/J | S | N |
| K | B | D | F | L |
| M | V | W | X | Z |
The matrix is constructed by writing the passphrase into the matrix cells from left to right and top to bottom, omitting any letters that have previously been used. It is filled out with the letters of the alphabet that do not occur in the passphrase, in alphabetical order. (In carrying out this process, “I” and “J” are identified, so we are effectively working over a 25-character alphabet.) Note that each letter of the alphabet occurs exactly once in the resulting matrix.
A message to be encrypted is first broken up into pairs of letters. For example, the message “MEET ME AT THE SUBWAY” would be broken into the pairs “ME” “ET” “ME” “AT” “TH” “ES” “UB” “WA” “YX”. Note that we have padded the message with a trailing “X” in order to make its length even, and spaces have been suppressed. Now, each pair of plaintext letters is encrypted. For example, the pair “AT” would be encrypted by taking the rectangle with “A” and “T” as its corners and then using the letters from the other two corners as the cipher text. In this example, the encryption of “AT” is “EY”. Decryption is by a similar procedure. The cipher also contains rules for handling various special cases such as when both plaintext letters occur in the same row or the same column or both. In decrypting, one also must resolve the I/J ambiguity and figure out when to remove the padding character.
The Hill cipher is another example of a cipher that encrypts groups of letters at once, thereby tending to mask letter frequencies. It is based on linear algebra. The key is, say, a non-singular 3 × 3 matrix K. The message m is divided into vectors mi of 3 letters each. Encryption is just the matrix-vector product Kv. Decryption is the same using K-1.
Unfortunately, the Hill cipher succumbs to a known plaintext attack. Given three linearly independent vectors m1, m2, and m3 and the corresponding ciphertexts ci = Kmi, i = 1,2,3, it is straightforward to solve for K.
Another way to strengthen monoalphabetic ciphers is to use different substitutions for different letter positions. For example, one might choose 10 different alphabet permutations k1,…,k10, use k1 for the first letter of m, k2 for the second letter, and so forth, repeating this sequence after every 10 letters. While this is much harder to break than monoalphabetic ciphers, it turns out that letter frequency analysis can still be used. Every 10th letter is encrypted using the same permutation, so the submessage consisting of just those letters still exhibits normal English language letter frequencies.
All of the methods discussed so far are based on letter substitution. Another technique is to rearrange the letters of the plaintext. For example, one might write a plaintext message into a matrix by rows and then read it out by columns. While transposition does not seem like a very powerful technique by itself, when used in combination with substitution techniques it can be quite effective. Most practical symmetric cryptosystems are built by composing together many stages of substitutions and transpositions.
Ciphers can be composed to create new ciphers. For example, suppose (E1,D1) and (E2,D2) are two ciphers. The composition is the cipher (E,D) with keys of the form k = (k1,k2), where
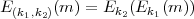
and similarly,
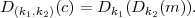
This may lead to a stronger cipher or it may not, and it can be difficult to analyze. Indeed, practical symmetric cryptosystems such as DES and AES tend to be built in this modular way as a composition of simpler systems. Each component offers little security by itself, but when composed, the layers obscure the message to the point that it is difficult for an adversary to recover. The trick is to find ciphers that do successfully hide useful information from a would-be attacker when used in concert.
To illustrate that composition doesn’t always increase the strength of a cipher, let’s consider double Caeser, which is simply the Caeser cipher composed with itself. One might hope that double Caeser is more resistant to a brute force attack since now there are 262 = 676 possible key pairs (k1,k2). Unfortunately, that is not the case, for there are still only 26 possible decryptions of each ciphertext. This is because the double Caeser encryption function EE(k1,k2) is the same as the single Caeser encryption function Ek with key k = (k1 + k2) mod 26. Even though the key space was enlarged, the number of distinct encryption functions was not.