25 Data Encryption Standard (DES)

The Data Encryption Standard is a block cipher that operates on 64-bit blocks and uses a 56-bit key. It was the standard algorithm for data encryption for over 20 years until it became widely acknowledged that the key length was too short and it was subject to brute force attack. (The new standard used the Rijndael algorithm and is called AES.)

25.1 Feistel Networks

DES is based on a Feistel network. This is a general method for building an invertible function from any function f that scrambles bits. It consists of some number of stages. Each stage i maps a pair of 32-bit words (L_i,R_i) to a new pair (L_i+1,R_i+1). By applying the stages in sequence, a t-stage network maps (L₀,R₀) to (L_t,R_t). The (L₀,R₀) is the plaintext, and (L_t,R_t) is the corresponding ciphertext.

Each stage works as follows:

(1)

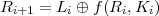(2)

Here, K_i is a subkey, which is generally derived in some systematic way from the master key k.

The security of a Feistel-based code lies in the construction of the function f and in the method for producing the subkeys K_i, However, the invertibility follows just from properties of ⊕.

The inversion problem is to find (L_i,R_i) given (L_i+1,R_i+1). Equation 1 gives us R_i. Knowing R_i and K_i, we can compute f(R_i,K_i). We can then solve equation 2 to get

DES uses a 16 stage Feistel network. The pair L₀R₀ is constructed from a 64-bit message by a fixed initial permutation IP. The ciphertext output is obtained by applying IP^-1 to R₁₆L₁₆.

The scrambling function f(R_i,K_i) operates on a 32-bit data block and a 48-bit key block. Thus, a total of 48 × 16 = 768 key bits are used. They are all derived in a systematic way from the 56-bit primary key and are far from independent of each other.

25.2 The Scrambling Function

The scrambling function f(R_i,K_i) is the heart of DES. It operates on a 32-bit data block and a 48-bit key block. Thus, a total of 48 × 16 = 768 key bits are used. They are all derived in a systematic way from the 56-bit master key k and are far from independent of each other. In a little more detail, k is split into two 28-bit pieces C and D. At each stage, C and D are rotated by one or two bit positions. Subkey K_i is then obtained by applying a fixed permutation (transposition) to CD. (See Table 3.4c of the text.)

The scrambling function itself is rather involved. However, at its heart are eight “S-boxes”. These are boxes with 6 binary inputs c₀,x₁,x₂,x₃,x₄,c₁ and 4 binary outputs y₁,y₂,y₃,y₄. Each computes some fixed function in {0,1}⁶ →{0,1}⁴. Moreover, each S-box has the very special property that for each of the four possible ways of fixing the values of (c₀,c₁) to Boolean constants, the resulting function on the remaining four inputs x₁,…,x₄ is a permutation from {0,1}⁴ →{0,1}⁴. Therefore, we can regard an S-box as performing a substitution on four-bit “characters”, where the substitution performed depends both on the structure of the particular S-box and on the values of its “control inputs” c₀ and c₁. The eight S-boxes are all different and are specified by their truth tables.

The S-boxes together have a total of 48 input lines. Each of these lines is the output of a corresponding ⊕-gate. One input of each of these ⊕-gates is connected to a corresponding bit of the 48-bit subkey K_i. (This is the only place that the key enters into DES.) The other input of each ⊕-gate is connected to one of the 32 bits of the first argument of f. Since there are 48 ⊕-gates and only 32 bits in the first argument to f, some of those bits get used more than once. The mapping of input bits to ⊕-gates is called the expansion permutation E and is given by Table 3.2(c) in the text. By looking at the table, one sees that the ⊕-gates connected to the six inputs c₀,x₁,x₂,x₃,x₄,c₁ for S-box 1 are in turn connected to the input bits 32,1,2,3,4,5, respectively. For S-box 2, they go to bits 4,5,6,7,8,9, etc. Thus, inputs bits 1,4,5,8,9,…28,29,32 are each used twice, and the remaining input bits are each used once.

Finally, the 32 bits of output from the S-boxes are passed through a fixed permutation P (transposition) that spreads out the output bits. The outputs of a single S-box at one stage of DES become inputs to several different S-boxes at the next stage. This helps provide the desirable “avalanche” effect described in the text.

25.3 Security considerations

We have mentioned previously that DES is vulnerable to a brute force attack because of its small key size of only 56 bits. However, it has turned out to be remarkably resistant to two recently discovered cryptanalysis attacks, differential cryptanalysis and linear cryptanalysis. The former can break DES using “only” 2⁴⁷ chosen ciphertext pairs. The latter works with 2⁴³ chosen plaintext pairs. Neither attack is feasible in practice.

DES has now been replaced as a national standard by the new AES (Advanced Encryption Standard), based on the Rijndael algorithm, developed by two Dutch computer scientists. AES supports key sizes of 128, 192, and 256 bits and works on 128-bit blocks. We will say more about it later in the course.

26 Double Encryption and Group Property

A natural way to attempt to increase the security of a cryptosystem is double encryption. Each message is encrypted twice using two different keys k₁ and k₂. That is, c = E_k2(E_k1(m). Now, a brute force attack would require trying all possible keys k₁ and all possible keys k₂, thereby doubling the effective key length. In the case of DES, this would result in a key length of 112 which is plenty large enough to make a full enumeration of the key space infeasible.

Unfortunately, double encryption does not increase the security of a cryptosystem as much as one might naively think. The reason is that it allows new kinds of attacks that are more efficient than brute force.

We consider two cases: When the underlying cryptosystem is a group, and when it is not. DES has been shown not to be a group.

26.1 Group property and birthday attacks

Double encryption is really a new cryptosystem created by composing two encryption functions. Let = (k₁,k₂) be the key of the double encryption system, and let Ê_k denote the resulting encryption function, that is,

Combining two functions in this way to define a new function is called functional composition. We often write Ê = E_k2 ∘ E_k1 to denote the result of composing E_k2 with E_k1.

Let = {E_k() ∣ k } be the set of possible encryption functions of the original cryptosystem, where is the key space. It might happen that Ê() = E_k() for some k . That is, there might be a key k of the original cryptosystem such that encrypting any message m with it gives the same ciphertext as encrypting m first with k₁ and then with k₂. If this is the case for every k₁,k₂ , then the original cryptosystem is said to be closed under functional composition, and we say that it is a group.

When the cryptosystem is a group, double encryption adds no security against a brute force attack. Even though the key length has doubled, the number of distinct encryption functions has not increased (and might actually have decreased). Since every double encryption is same as a single encryption, the double encryption system will fall to a brute force attack on the original cryptosystem.

But it’s even worse. If a cryptosystem system is a group, then it is subject to a known plaintext “birthday” attack,¹ which reduces the number of keys that must be tried to roughly the square root of what a brute force attack needs. For example, if the original key length was 56, then only about 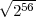= 2²⁸ keys need be tried.

Briefly, here’s how it works: Let (m,c) be a known plaintext-ciphertext pair. Choose 2²⁸ random keys k₁ and encrypt m using each. Choose another 2²⁸ random keys k₂ and decrypt c using each. Look for a match between these two sets. Assuming reasonable randomness properties of the encryption function, there is a significant probability of finding k₁ and k₂ such that E_k1(m) = D_k2(c). But this implies that E_k2(E_k1(m)) = c. In this case, we have succeeded in finding one key pair that works. In all likelihood there are not many pairs that do work, so with significant probability we have cracked the system. Using additional plaintext-ciphertext pairs, we can verify that we have likely found the correct key pair, or repeat this process again if we have not yet succeeded. I’ve glossed over many assumptions and details, but that’s the basic idea.

The drawback to the birthday attack (from the attacker’s perspective) is that it requires a lot of storage in order to find a matching element. Nevertheless, if DES were a group, this attack could be carried out in about a gigabyte of storage, easily within the storage capacity of modern workstations.

26.2 What happens when original system is not a group?

Even if the original system is not a group, double encryption still does not result in a cryptosystem with twice the effective key length. The reason is another “birthday”-style known-plaintext attack.

Let’s consider the case of double DES. As before, we start with a known plaintext-ciphertext pair (m,c). We carry out a birthday attack by encrypting m under many different keys, decrypting c under many different keys, and hope we find a matching element in the resulting two sets. Unlike the attack described in section 26.1, we encrypt m and decrypt c using all possible DES keys. Thus, we are guaranteed of finding at least one match, since if (k₁,k₂) is the real key pair used in the double encryption, then E_k1(m) = D_k2(c). If there is only one match, then we have found the key pair and broken the system. If there are several matches, we know that the key pair is one of the matching pairs. This set is likely to be much much smaller than 2⁵⁶, so they can each be tried on additional plaintext-ciphertext pairs to find which ones work. (Note that there might be more than one key pair that results in the same encryption function. In that case, we won’t be able to know which key pair Alice actually used in generating the ciphertexts, but we will be able to find a pair that is just as good and that lets us decrypt her messages.)

27 Triple DES

Three key triple DES (3TDES) avoids the birthday attack by using three DES encryptions, i.e., E_k3(E_k2(E_k1(m))), giving it an actual key length of 168 bits. While considerably more secure than single DES, for which a brute force attack requires only 2⁵⁶ decryptions, 3TDES can be broken (in principle) by a known plaintext attack using about 2⁹⁰ single DES encryptions and 2¹¹³ steps. While this attack is still not practical, the effective security thus lies in the range between 90 and 113, which is much smaller than the apparent 168 bits.²

A variant of triple DES in which the middle step is a decryption instead of an encryption is known as TDES-EDE, i.e., E_k3(D_k2(E_k1(m))). The variant does not affect the security, but it means that TDES-EDE encryption and decryption functions can be used to perform single DES encryptions and decryptions by taking k₁ = k₂ = k₃ = k, where k is the single DES key.

Another variant, two key triple DES (2TDES) uses only two keys k₁ and k₂, taking k₃ = k₁. However, known plaintext attacks or chosen plaintext attacks reduce the effective security to only 80 bits. See Wikipedia for further information on triple DES.

28 Block Ciphers

A b-bit block cipher takes as inputs a key and a b-bit plaintext block and produces a b-bit ciphertext block as output. Most of the ciphers we have been discussing so far are of this type. Block ciphers typically operate on fairly long blocks, e.g., 64-bits for DES, 128-bits for Rijndael (AES). Block ciphers can be designed to resist known-plaintext attacks and can therefore be pretty secure, even if the same key is used to encrypt a succession of blocks, as is often the case.

Of course, the length messages one wants to send are rarely exactly the block length. To use a block cipher to encrypt long messages, one first divides the message into blocks of the right length, padding the last partial block according to a suitable padding rule. Then the block cipher is used in some chaining mode to encrypt the sequence of resulting blocks. A chaining mode tells how to encrypt a sequence of plaintext blocks m₁,m₂,…,m_t to produce a corresponding sequence of ciphertext blocks c₁,c₂,…,c_t, and conversely, how to recover the m_i’s given the c_i’s.

Padding involves more than just sticking 0’s on the end of a message until its length is a multiple of the block length. The reason is that one must be able to recover the original message from the padded version. If one tacks on a variable number of 0’s during padding, how many are to be removed at the end? To solve this problem, a padding rule must include the information about how much padding was added. There are many ways to do this. One way is to pad each message with a string of 0’s followed by a fixed-length binary representation of the number of 0’s added. For example, if the block length is 64, then at most 63 0’s ever need to be added, so a 6-bit length field is sufficient. A message m is then padded to become m′ = m ⋅ 0^k ⋅k, where k is a number in the range [0,63] and k is its representation as a 6-bit binary number. k is then chosen so that ∣m′∣ = ∣m∣ + k + 6 is a multiple of b.

Some standard chaining modes are:

• Electronic Codebook Mode (ECB) – apply cipher to each plaintext block. That is, c_i = E_k(m_i) for each i. This becomes in effect a monoalphabetic cipher, where the “alphabet” is the set of all possible blocks and the permutation is defined by E_k. To decrypt, Bob computes m_i = D_k(c_i).
• Cipher Block Chaining Mode (CBC) – encrypt the XOR of the current plaintext block with the previous ciphertext block to produce the current ciphertext block. That is, c_i = E_k(m_i⊕c_i-1). To get started, we take c₀ = IV , where IV is a fixed initialization vector which we assume is publicly known. To decrypt, Bob computes m_i = D_k(c_i) ⊕ c_i-1.
• Cipher-Feedback Mode (CFB) – XOR the current plaintext block with the encryption of the previous ciphertext block. That is, c_i = m_i⊕E_k(c_i-1), where again, c₀ is a fixed initialization vector. To decrypt, Bob computes m_i = c_i ⊕ E_k(c_i-1). Note that Bob is able to decrypt without using the block decryption function D_k. In fact, it is not even necessary for E_k to be a one-to-one function (but using a non one-to-one function might weaken security).
• Output Feedback Mode (OFB) – the encryption function is iterated on an initial vector (IV) to produce a stream of block keys, which in turn are XORed with the successive plaintext blocks to produce the successive ciphertext blocks. (This is similar to a simple keystream generator.) That is, c_i = m_i ⊕ k_i, where k_i = E_k(k_i-1) is a block key. k₀ is a fixed initialization vector IV. To decrypt, Bob can apply exactly the same method to the ciphertext to get the plaintext, that is, m_i = c_i ⊕ k_i, where k_i = E_k(k_i-1).
• Propagating Cipher-Block Chaining Mode (PCBC) – encrypt the XOR of the current plaintext block, previous plaintext block, and previous ciphertext block. That is, c_i = E_k(m_i ⊕ m_i-1⊕c_i-1). Here, both m₀ and c₀ are fixed initialization vectors. To decrypt, Bob computes m_i = D_k(c_i) ⊕ m_i-1 ⊕ c_i-1.

Remarks

1. Both CFB and OFB are closely related to stream ciphers since in both cases, c_i is m_i XORed with some function of stuff that came before stage i. Like a one-time pad and other simple XOR stream ciphers, OFB becomes insecure if the same key is ever reused, for the sequence of k_i’s generated will be the same. CFB, however, avoids this problem, for even if the same key k is used for two different message sequences m_i and m′_i, it will not generally be the case that m_i ⊕ m′_i = c_i ⊕ c′_i; rather, m_i ⊕ m′_i = c_i ⊕ c′_i ⊕ E_k(c_i-1) ⊕ E_k(c′_i-1), and the dependency on k does not drop out.
2. The different modes differ in their sensitivity to data corruption. With ECB and OFB, if Bob receives a bad block c_i, then he cannot recover the corresponding m_i, but all good ciphertext blocks can be decrypted. With CBC and CFB, he needs both good c_i and c_i-1 blocks in order to decrypt m_i. Therefore, a bad block c_i renders both m_i and m_i+1 unreadable. With PCBC, a bad block c_i renders m_j unreadable for all j ≥ i.
3. Other modes can be easily invented. We see that in all cases, c_i is computed by some expression (which may depend on i) built from E_k() and ⊕ applied to blocks c₁,…,c_i-1, m₁,…,m_i, and the initialization vectors. Any such equation that can be “solved” for m_i (by possibly using D_k() to invert E_k()) is a suitable chaining mode in the sense that Alice is able to produce the ciphertext and Bob is able to decrypt it. Of course, the resulting security properties depend heavily on the particular expression chosen.