29 Stream Ciphers

Symmetric (one-key) cryptosystems fall into two broad classes, block ciphers and stream ciphers. Recall that a block cipher encrypts large blocks of data at a time. Most of the ciphers we have been discussing so far are of this type. A stream cipher on the other hand process a stream of characters in an on-line fashion, emitting the ciphertext characters as it goes.

A stream cipher has two components, the cipher that is used to encrypt a given character, and a keystream generator that produces a different key to be used for each successive letter.

A simple stream cipher can be built from the XOR cryptosystem used in the one-time pad. However, rather than using a random key as long as the message, we instead generate the keystream on the fly using a state machine. A keystream generator consists of three parts: an internal state, a next-state generator, and an output function. The next-state generator and output functions can both depend on (original) master key. At each stage, the state is updated and the output function applied to obtain the next component of the keystream. Like a one-time pad, one must use different key for each message; otherwise the system is easy to break.

To be secure, the keystream generator must be a good pseudorandom sequence generator. Any regularities in the output of the keystream generator will give an attacker information about the plaintext. In particular, if the attacker is ever able to figure out the internal state of the keystream generator, then she will be able to predict all future outputs of the generator and decipher the remainder of the ciphertext. It turns out that the linear congruential pseudorandom number generators typically found in software libraries are quite insecure. After observing a relatively short sequence of outputs from the generator, one can solve for the state and correctly predict all future outputs. For the simple XOR cipher to be secure, a cryptographically strong pseudorandom number generator must be used. Even so, the fact that a different key must be used for each message sent makes it problematic in practice.

A possible improvement would be to make the next-state generator depend on the current plaintext or ciphertext characters so that the generated keystreams will diverge on different messages, even if the key is the same. However, this has the disadvantage that one bad ciphertext character will render the rest of the message undecipherable to Bob since he can no longer know what the current state is.

Output Feedback (OFB) block chaining mode, described in Lecture 5, essentially turns a block cipher into an XOR stream cipher on blocks, for the successive block keys k_i depend only on the master key and i, not on the message or ciphertext.

30 Stream Ciphers from CFB and OFB Modes

OFB and CFB block chaining modes can be naturally extended to stream ciphers on units smaller than full blocks. The idea is to use a shift register X to accumulate the feedback bits from previous stages of encryption so that the full-sized blocks needed by the block chaining method are available. X is initialized to some public initialization vector.

Assume for sake of discussion a 64-bit block size for the underlying block cipher and a character size of s-bits. (Think of s = 8.) Let B = {0,1}. We define two operations: L_m and R_m : B⁶⁴ → B^m. L_m(x) are the leftmost m bits of x, and R_m(x) are the rightmost m bits of x.

The extended version of CFB and OFB are very similar. Both compute a byte key k_i and use it to encrypt message byte m_i with a simple XOR cipher. That is, c_i = m_i ⊕ k_i. In both modes, k_i can be computed knowing only the ciphertext and master key, so Bob computes k_i and then decrypts by computing m_i = c_i ⊕k_i. Finally, both modes compute k_i = L_s(E_k(X_i)) where X_i is the new contents of the shift register at stage i. The two modes differ in how they update the shift register. In extended CFB mode,

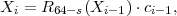
where ‘⋅’ denotes concatenation. In extended OFB mode,

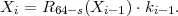
Thus, CFB updates X using the previous ciphertext byte, whereas OFB updates it using the previous byte key.

The differences between the two modes seem minor, but they have profound implications on the resulting cryptosystem. In CFB mode, the loss of ciphertext byte c_i will cause m_i and several succeeding message bytes to become undecipherable. At first sight it might seem that all future message bytes would be lost, but if one looks carefully at the shift register updating algorithm, one sees that X_j = c_j-8c_j-7…c_j-2c_j-1 (in our special case of s = 8), so it depends on only the last eight ciphertext bytes. Hence, Bob will be able to recover plaintext bytes beginning with m_i+8 after the loss of c_i. In OFB mode, X_i depends only on i and the master key k (and the initialization vector IV), so loss of a ciphertext byte causes loss of only the corresponding plaintext byte.

The downside of OFB is the same as for the one-time pad and other simple XOR ciphers, namely, if two message streams are encrypted using the same master key, then the XOR of their encryptions is the same as the XOR of the plaintexts. This allows Eve to recover potentially useful information about the plaintexts and renders the method vulnerable to a known plaintext attack. CFB does not suffer from this problem since different messages lead to different ciphertexts and hence different key streams. However, even CFB mode has the undesirable property that the key streams will be the same up to and including the first byte in which the two message streams differ. This will enable Eve to determine the length of the common prefix of the two message streams and also to determine the XOR of the first bytes at which they differ.

One way around this problem in both ciphers is to use a different initialization vector for each message. The IV is sent to Bob in the clear, along with the ciphertext. X = X₀ is initialized to IV, then k₀ = L_s(E_k(X₀)) is computed, and then normal encryption proceeds.

31 Rotor machines

Rotor machines are mechanical devices for implementing stream ciphers. They played an important role during the Second World War. The Germans believed their Enigma machine (Figure 1) was unbreakable, but the Allies, with great effort, succeeded in breaking it and in reading many of the top-secret military communications. This is said to have changed the course of the war.

The basic idea of a rotor machine is to use electrical switches to create a permutation of 26 input wires to 26 output wires. Each input wire is attached to a key on a keyboard. Each output wire is attached to a lamp. The keys are associated with letters just like on a computer keyboard. Each lamp is also labeled by a letter from the alphabet. Pressing a key on the keyboard causes one of the lamps to light, which indicates the ciphertext character corresponding to the key pressed. The operator types the message one character at a time and writes down for each letter the corresponding lamp. To decrypt, one could switch inputs and outputs to obtain the inverse permutation, type in the ciphertext, and read out the plaintext.

What I have described so far is just an electro-mechanical device for implementing a monoalphabetic cipher. However, rotor machine gain their power by changing the permutation after each letter. Each rotor is individually wired to produce some random-looking fixed permutation π. Several rotors stacked together produce the composition of the permutations implemented by the individual rotors. In addition, the rotors can rotate relative to each other, implementing in effect a rotation permutation (like the Caeser cipher uses). Let ρ_k(x) = x + k mod 26. Then rotor in position k implements permutation ρ_kπρ_k^-1. Several rotors could be stacked together to implement the composition of the permutations computed by each. For example, three rotors implementing permutations π₁, π₂, and π₃, placed in positions r₁, r₂, and r₃, respectively, would produce the permutation

After each letter is typed, some of the rotors change position, much like the mechanical odometer used in older cars. The period before the rotor positions repeat is quite long, allowing long messages to be sent without ever repeating the same permutation. Thus, a rotor machine is much like a polyalphabetic substitution cipher, but with a very long period. However, unlike a pure polyalphabetic cipher, the successive permutations until the cycle repeats are not independent of each other but are related to each other by (1). This gives the first toehold into methods for breaking the cipher (which are far beyond the scope of this course).

Several different kinds of rotor machines were built and used, both by the Germans and by others, some of which work somewhat differently from what I described above. However, the basic principles are the same. The interested reader can find much detailed material on the web by searching for “enigma cipher machine” and “rotor cipher machine”. Nice descriptions may be found at http://en.wikipedia.org/wiki/Enigma_machine and http://www.quadibloc.com/crypto/intro.htm.

32 Steganography

Steganography, hiding one message inside another, is an old technique that is still in use. For example, a message can be hidden inside a graphics image file by using the low-order bit of each pixel to encode the message. The visual effect of these tiny changes is probably too small to be noticed by the user. The message can be hidden further by compressing it or by encrypting it with a conventional cryptosystem. Unlike conventional cryptosystems, where we assume the attacker knows everything about the cryptosystem except for the secret key, steganography relies on the secrecy of the method of hiding for its security. If Eve does not even recognize the message as ciphertext, then she is not likely to attempt to decrypt it.

33 Attacks by Malicious Active Adversaries

So far in the course, we have mostly been discussing a single cryptographic application, namely, secret message transmission from Alice to Bob over a a publicly-readable channel. Our goal has been to maintain privacy in the face of a passive eavesdropper Eve. Once we assume an active adversary “Mallory” who has the power to modify messages and generate his own messages as well as eavesdrop, life becomes more difficult.

Encryption alone no longer solves Alice and Bob’s problem. Alice sends c = E_k(m), but Bob may receive a corrupted or forged c′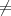c. How then does Bob know that the message he receives really was sent by Alice?

The naive answer is that Bob computes m′ = D_k(c′), and if m′ “looks like” a valid message, then Bob accepts it as having come from Alice. The reasoning here is that Mallory, not knowing k, could not possibly have produced a valid-looking message.

For any particular cipher such as DES, that assumption may or may not be valid, but here are two things to watch out for:

1. There are three successively easier possible attacks in which Mallory might produce fraudulent messages:
   1. He might produce c′ = E_k(m′) for a message m′ of his choosing.
   2. He might produce a message c′ for which the corresponding plaintext m′ is a valid message, even though he could not choose m′ in advance, nor perhaps he does not even know what m′ is.
   3. He might be able to alter a legitimate message c from Alice to produce a new message c′ that corresponds to an altered form m′ of the true message m. For example, if m represents an amount of money, it is conceivable that Mallory could find the encryption of m + 1 given the encryption of m, without knowing either m or m + 1.

   Attack (1a) is similar to, but not the same as, the notion of breaking the cryptosystem that we have been studying. We have been asking that it be hard for Eve to compute m = D_k(c) knowing c but not k. To carry out attack (1a) requires that Mallory compute E_k(m) knowing m but not k. It’s conceivable that he could do the latter without being able to do the former.

   One form of attack (1b) clearly is possible, the so-called replay attack. This is when Mallory substitutes a legitimate old encrypted message c′ for the current message c. It can be thwarted by adding timestamps and/or sequence numbers to the messages, so that Bob can recognize when old messages are being received. Of course, this only works if Alice and Bob anticipate the attack and incorporate appropriate countermeasures into the protocol they are using.

   However, even if replay attacks are ruled out, a cryptosystem that is secure against attack (1a) might still permit attack (1b). There are all sorts of ways that Mallory can generate values c′. What gives us confidence that Bob won’t accept one of them as being valid?

   Attack (1c) might be possible even in a cryptosystem that is free from attacks (1a) and (1b). For example, if c₁ and c₂ are encryptions of valid messages, perhaps so is c₁ ⊕ c₂. Whether or not it is depends entirely on particular properties of E_k. It does not follow in general from the difficulty of decrypting a given ciphertext. We will see some cryptosystems later which do have the property of being vulnerable to attack (1c). In some contexts, this can actually be a useful property, as we will see.

2. Cryptosystems are not always used to send natural language or other highly-redundant messages. For example, suppose Alice wants to send Bob her password to a web site. Knowing full well the dangers of sending passwords in the clear over the internet, she chooses to encrypt it instead. Since passwords are supposed to look like random strings of characters, Bob will likely accept anything he gets from Alice. He could be quite embarrassed (or worse) claiming he knew the correct password when in fact the password he thought was from Alice was actually a fraudulent one derived from a random ciphertext c′ produced by Mallory.

34 Message authentication codes (MACs)

What Alice and Bob need to solve their problem is called a Message Authentication Code or MAC. A MAC is generated by a function function C_k(m) that can be computed by anyone knowing a secret key k. However, it should be hard for an attacker to find any pair (m,ξ) such that ξ = C_k(m) without knowing k. In fact, this should remain hard even if the attacker knows a set of valid MAC pairs {(m₁,ξ₁),…,(m_t,ξ_t)} that Alice previously sent, so long as m itself is not the message in one of the known pairs.

A block cipher such as DES can be used to compute a MAC by making use of one of the ciphertext chaining modes, CBC or CFB. (See Lecture notes 5.) In these modes, the last ciphertext block c_t depends on all t message blocks m₁,…,m_t. Therefore, we define C_k(m) = c_t. The result of this process is reputed to be a good MAC generation function. Note that the MAC is only a single block long, which in general is much shorter than the message. A MAC acts like a checksum for preserving data integrity, but it has the advantage that an adversary cannot compute a valid MAC for an altered message.

Using a MAC, Alice can send a message m in the clear and also send ξ = C_k(m). Bob receives m′ and ξ′, possibly different from what Alice sent. Bob checks that ξ′ = C_k(m′) and if so, accepts m′ as a valid message from Alice. We say that Mallory successfully cheats if Bob accepts a message m′ as valid that Alice never sent. The assumed property of a MAC is that Mallory cannot do this, even knowing a set of valid MAC pairs previously sent by Alice. In this application, the MAC is used to prevent forgery of messages, not for protection of privacy.

If Alice wants both privacy and authenticity, she can encrypt m and use the MAC to protect the ciphertext from alteration. Thus, Alice sends c = E_k(m) and ξ = C_k(c). Bob, after receiving c′ and ξ′, only decrypts c′ after first verifying that ξ′ = C_k(c′).

Another possiblility is for Alice to send c = E_k(m) and ξ = C_k(m). Here, the MAC is computed from m, not c. Bob, upon receiving c′ and ξ′, first decrypts c′ to get m′ and then checks that ξ′ = C_k(m′). In practice, this might also work, but its security does not follow from the assumed security property of the MAC. Even if Mallory cannot produce a pair (m′,ξ′) for an m′ that Alice never sent, it does not follow that he cannot produce a pair (c′,ξ′) such that c′ is not the encryption of one of Alice’s messags, yet Bob will accept c′ as valid. If he succeeds is doing this, then Bob will decrypt c′ to get m′ = D_k(c′), and incorrectly accept m′ as coming from Alice.

Note that this kind of forgery is indeed possible if, for example, the MAC function C_k and the encryption function E_k are the same. In that case, C_k(D_k(c′)) = E_k(D_k(c′)) = c′, and Bob accepts every pair (c′,c′) as valid, completely defeating the purpose of the MAC.¹ A more likely example where forgery would be possible would be if C_k were derived from E_k using the CBC or CFB chaining modes as described above, for then the MAC is just the last ciphertext block c′_t, and Bob would accept (c′,c′_t) as valid.