50 Tests of Compositeness: Formal Definition

Formally, a test of compositeness is a set T = {τ₁,…,τ_s}, where τ_i : Z →{true, false} has the property that

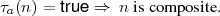
If τ_a(n) = true, we say that τ_a(n) succeeds, and a is a witness to the compositeness of n. If τ_a(n) = false, then the test fails and gives no information about the compositeness of n. Clearly, if n is prime, then all τ_a fail on n, but if n is composite, then τ_a(n) may either succeed or fail.

A test of compositeness T is useful if there is a feasible algorithm T(n,a) that computes τ_a(n), and for every composite number n, a fraction c > 0 of the tests succeed on n. Suppose for simplicity that c = 1∕2 and one applies 100 randomly-chosen tests to n. If any of them succeeds, we have a proof that n is composite. If all fail, we don’t know whether or not n is prime or composite. But what we do know is that if n is composite, the probability that all 100 tests fail is only 1∕2¹⁰⁰.

In practice, what we do to choose RSA primes p and q is to choose numbers at random and apply some fixed number of randomly-chosen tests to each candidate,¹ rejecting the candidate if it proves to be composite. We keep the candidate (and assume it to be prime) if all of the tests for compositeness fail. We never know whether or not our resulting numbers p and q really are prime, but we can adjust the parameters to reduce the probability to an acceptable level that we will end up a number p or q that is not prime (and hence that we have unknowingly generated a bad RSA key).

51 Example Tests of Compositeness

Here are two examples of tests for compositeness.

1. Let δ_a(n) = (2 ≤ a ≤ n - 1 and a∣n). Test δ_a succeeds on n if a is a proper divisor of n, which indeed implies that n is composite. Thus, {δ_a}_aZ is a valid test of compositeness. Unfortunately, it isn’t very useful in a probabilistic primality algorithm since the number of tests that succeed when n is composite are too small. For example, if n = pq for p,q prime, then the only tests that succeed are δ_p and δ_q.
2. Let ζ_a(n) = (2 ≤ a ≤ n - 1 and a^n-1 ⁄≡ 1 (mod n). By Fermat’s theorem, if p is prime and gcd(a,p) = 1, then a^p-1 ≡ 1 (mod p). Hence, if ζ_a(n) succeeds, it must be the case that n is not prime. This shows that {ζ_a}_aZ is a valid test of compositeness. For this test to be adequate for a probabilistic primality algorithm, we would need to know that for all composite numbers n, a significant fraction of the tests ζ_a succeed on n. Unfortunately, there are certain compositeness numbers n called pseudoprimes for which all of the tests ζ_a fail. Such n are fairly rare, but they do exist. The ζ_a tests are unable to distinguish pseudoprimes from true primes, so they are not adequate for testing primality.

We will return to this topic later when we have developed sufficient number theory to present tests of compositeness that do have the properties needed to make them useful in probabilistic primality algorithms.

52 Chinese Remainder Theorem

We now return to a basic result of number theory that will be used later.

Let n₁,n₂,…,n_k be positive pairwise relatively prime positive integers² , let n = ∏ _i=1^kn_i, and let a_i Z_i for i = 1,…,k. Consider the system of congruence equations with unknown x:

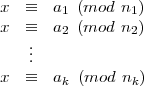(1)

The Chinese Remainder Theorem says that (1) has a unique solution in Z_n.

To solve for x, let

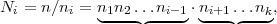
and compute M_i = N_i^-1 mod n_i, for 1 ≤ i ≤ k. Note that N_i^-1 (mod n_i) exists since gcd(N_i,n_i) = 1 by the pairwise relatively prime condition. We can compute N_i^-1 using the methods of section 46 (lecture notes 9). Now let

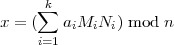(2)

If j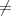i, then M_jN_j ≡ 0 (mod n_i) since n_i∣N_j. On the other hand, M_iN_i ≡ 1 (mod n_i) by definition of M_i. Hence,

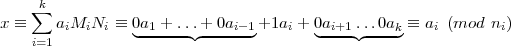(3)

for all 1 ≤ i ≤ k, establishing that (2) is a solution of (1).

To see that the solution is unique in Z_n, let χ be the mapping x(x mod n₁,…,x mod n_k). χ is a surjection³ from Z_n to Z_n1 ×…× Z_nk since we have just shown for all (a₁,…,a_k) Z_n1 ×…× Z_nk that there exists x Z_n such that χ(x) = (a₁,…,a_k). Since also ∣Z_n∣ = ∣Z_n1 ×…×Z_nk∣, χ is a bijection, and (1) has only one solution in Z_n.

53 Homomorphic property of χ

The bijection χ is interesting in its own right, for it establishes a one-to-one correspondence between members of Z_n and k-tuples (a₁,…,a_k) in Z_n1 ×… × Z_nk. This lets us reason about and compute with k-tuples and then translate the results back to Z_n.

The homomorphic property of χ means that performing an arithmetic operation on x Z_n corresponds to performing the similar operation on each of the components of χ(x). More precisely, let ⊙ be one of the arithmetic operations +, -, or ×. If χ(x) = (a₁,…,a_k) and χ(y) = (b₁,…,b_k), then

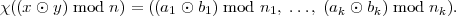(4)

In other words, if one first performs z = (x ⊙ y) mod n and then computes z mod n_i, the result is the same as if one instead first computed a_i = (x mod n_i) and b_i = (y mod n_i) and then performed (a_i ⊙ b_i) mod n_i. This relies on the fact that (z mod n) mod n_i = z mod n_i, which holds because n_i∣n.

54 RSA Decryption Works for All of Z_n

In section 42 (lecture notes 8), we showed that RSA decryption works when m,c Z*_n but omitted the proof that it actually works for all m,c Z_n. We now use the Chinese Remainder Theorem to supply this missing piece.

Let n = pq be an RSA modulus, p,q distinct primes, and let e and d be the RSA encryption and decryption exponents, respectively. We show m^ed ≡ m (mod n) for all m Z_n.

Define a = (m mod p) and b = (m mod q), so

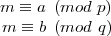(5)

Raising both sides to the power ed gives

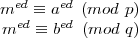(6)

We now argue that a^ed ≡ a (mod p). If a ≡ 0 (mod p), then obviously a^ed ≡ 0 ≡ a (mod p). If a ⁄≡ 0 (mod p), then gcd(a,p) = 1 since p is prime, so a Z*_p. By Euler’s theorem,

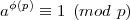
Since ed ≡ 1 (mod φ(n)), we have ed = 1 + uφ(n) = 1 + uφ(p)φ(q) for some integer u. Hence,

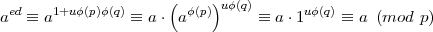(7)

Similarly,

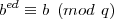(8)

Combining the pair (6) with (7) and (8) yields

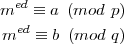
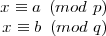(9)

From (5), m is also a solution of (9). By the Chinese Remainder Theorem, the solution to (9) is unique modulo n, so m^ed ≡ m (mod n) as desired.

55 RSA Security

Several possible attacks on RSA are discussed below and their relative computational difficulties discussed.

55.1 Factoring n

The security of RSA depends on the computational difficulty of several different problems, corresponding to different ways that Eve might attempt to break the system. The first of these is the RSA factoring problem: Given a number n that is known to be the product of two primes p and q, find p and q. Clearly if Eve can find p and q, then she can compute the decryption key d from the public encryption key e (in the same way that Alice did when generating the key) and subsequently decrypt all ciphertexts.

55.2 Computing φ(n)

Eve doesn’t really need to know the factors of n in order to compute d. It is enough for her to know φ(n). Computing φ(n) is no harder than factoring n since φ(n) is easily computed given the factors of n, but is it perhaps easier? If it were, then Eve would have a possible attack on RSA different from factoring n. It turns out that it is not easier, for if Even knows φ(n), then she can factor n. She simply sets up the system of quadratic equations

55.3 Finding d

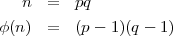
Another possibility is that Eve might somehow be able to compute d from e and n even without the ability to factor n or compute φ(n). That would represent yet another attack that couldn’t be ruled out by the assumption that the RSA factoring problem is hard. However, that too is not possible, as we now show.

Suppose Eve knows n and e and is somehow able to obtain d. Then Eve can factor n by a probabilistic algorithm. The algorithm is presented in Figure1.

To factor n: /* Find s, t such that ed - 1 = 2st and t is odd */ s = 0; t = ed - 1; while (t is even ) {s++; t∕=2;} /* Search for non-trivial square root of 1 (mod n) */ do { /* Find a random square root b of 1 (mod n) */ choose a Z*n at random; b = at mod n; while (b2 ⁄≡ 1 (mod n)) b = b2 mod n; } while (b ≡±1 (mod n)); /* Factor n */ p = gcd(b - 1,n); q = n∕p; return (p,q); } Figure 1: Algorithm for factoring n given d.

We begin by finding unique integers s and t such that 2^st = ed- 1 and t is odd. This is always possible since ed - 1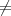0. One way to find s and t is to express ed - 1 in binary. Then s is the number of trailing zeros and t is the value of the binary number that remains after the trailing zeros are removed. Since ed - 1 ≡ 0 (mod φ(n)) and 4∣φ(n) (since both p - 1 and q - 1 are even), it follows that s ≥ 2.

Now, for each a chosen at random from Z*_n, define a sequence b₀,b₁,…,b_s, where b_i = a^2it mod n, 0 ≤ i ≤ s. Each number in the sequence is the square of the number preceding it modulo n. The last number in the sequence is 1 by Euler’s theorem and the fact that φ(n)∣(ed - 1). Since 1² mod n = 1, every element of the sequence following the first 1 is also 1. Hence, the sequence consists of a (possibly empty) block of non-1 elements, following by a block of 1’s.

It is easily verified that b₀ is the value of b when the innermost while loop is first entered, and b_k is the value of b after the k^th iteration of that loop. The loop executes at most s- 1 times since it terminates just before the first 1 is encounter, that is, when b² ≡ 1 (mod n). At this time, b = b_k is a square root of 1 (mod n).

Over the reals, we know that each positive number has two square roots, one positive and one negative, and no negative numbers have real square roots. Over Z*_n for n = pq, it turns out that 1∕4 of the numbers have square roots, and each number that has a square root actually has four. Since 1 does have a square root modulo n (itself), there are four possibilities for b: ±1 mod n and ±r mod n for some r Z*_n, r ⁄≡±1 (mod n).

The do loop terminates if and only if b ⁄≡±1 (mod n). At that point we can factor n. Since b² ≡ 1 (mod n), we have n∣(b² - 1) = (b + 1)(b- 1). But since b ⁄≡±1 (mod n), n does not divide b + 1 and n does not divide b - 1. Therefore, one of the factors of n divides b + 1 and the other divides b - 1. Hence, gcd(b - 1,n) is a non-trivial factor of n.

It can be shown that there is at least a 0.5 probability that b ⁄≡±1 (mod n) for the b computed by this algorithm in response to a randomly chosen a Z*_n. Hence, the expected number of iterations of the do loop is at most 2. (See Evangelos Kranakis, Primality and Cryptography, Theorem 5.1 for details.)

Here’s a simple example of the use of this algorithm. Suppose n = 5 × 11 = 55, e = 3, and d = 27. (These are possible RSA values since φ(n) = 40 and ed = 81 ≡ 1 (mod 40).) Then ed - 1 = 80 = (1010000)₂, so s = 4 and t = 5.

Now, suppose we take a = 2. We compute the sequence of b’s as follows:

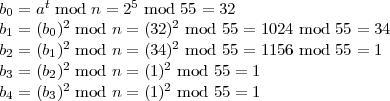
Since the last b_i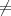1 in this sequence is 34, and 34 ⁄≡-1 (mod 55), then 34 is a non-trivial square root of 1 modulo 55. It follows that gcd(34 - 1,55) = 11 is a prime divisor of n.

55.4 Finding plaintext

Eve isn’t really interested in factoring n, computing φ(n), or finding d, except as a means to read Alice’s secret messages. Hence, the problem we would like to be hard is the problem of computing the plaintext m given an RSA public key (n,e) and a ciphertext c. The above shows that this problem is no harder than factoring n, computing φ(n), or finding d, but it does not rule out the possibility of some clever way of decrypting messages without actually finding the decryption key. Perhaps there is some feasible probabilistic algorithm that finds m with non-negligible probability, maybe not even for all ciphertexts c but for some non-negligible fraction of them. Such a method would “break” RSA and render it useless in practice. No such algorithm has been found, but neither has the possibility been ruled out, even under the assumption that the factoring problem itself is hard.