Claim 1 Let n = pq for p, q distinct odd primes. Then every a  QRn has exactly four square
roots in Z*
n, and exactly 1/4 of the elements of Z*n are quadratic residues.
QRn has exactly four square
roots in Z*
n, and exactly 1/4 of the elements of Z*n are quadratic residues.
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Notes 12 (rev. 1) | |
| Professor M. J. Fischer | October 17, 2006 | |
Lecture Notes 12
Claim 1 Let n = pq for p, q distinct odd primes. Then every a  QRn has exactly four square
roots in Z*
n, and exactly 1/4 of the elements of Z*n are quadratic residues.
QRn has exactly four square
roots in Z*
n, and exactly 1/4 of the elements of Z*n are quadratic residues.
Proof: Consider the mapping sq : Z*n → QRn defined by b b2 mod n. We show that this is a
4-to-1 mapping from Z*n onto QRn.
b2 mod n. We show that this is a
4-to-1 mapping from Z*n onto QRn.
Let a  QRn and let b2 ≡ a (mod n) be a square root of a. Then also b2 ≡ a (mod p)
and b2 ≡ a (mod q), so b is a square root of a (mod p) and b is a square root of a (mod q).
Conversely, if bp is a square root of a (mod p) and bq is a square root of a (mod q), then by
the Chinese Remainder theorem, the unique number b
QRn and let b2 ≡ a (mod n) be a square root of a. Then also b2 ≡ a (mod p)
and b2 ≡ a (mod q), so b is a square root of a (mod p) and b is a square root of a (mod q).
Conversely, if bp is a square root of a (mod p) and bq is a square root of a (mod q), then by
the Chinese Remainder theorem, the unique number b  Z*n such that b ≡ bp (mod p) and
b ≡ bq (mod q) is a square root of a (mod n). Since a has two square roots mod p and two square
roots mod q, it follows that a has four square roots mod n. Thus, sq() is a 4-to-1 function, and
∣QRn∣ =
Z*n such that b ≡ bp (mod p) and
b ≡ bq (mod q) is a square root of a (mod n). Since a has two square roots mod p and two square
roots mod q, it follows that a has four square roots mod n. Thus, sq() is a 4-to-1 function, and
∣QRn∣ = 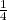 ∣Z*n∣ as desired. __
∣Z*n∣ as desired. __
There is a simple test due to Euler for whether a number is in QRp for p prime.
Proof: Let a ≡ b2 (mod p) for some b ⁄≡ 0 (mod p). Then
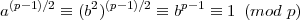
by Euler’s theorem, as desired.
For the other direction, suppose a(p-1)∕2 ≡ 1 (mod p). Clearly a ⁄≡ 0 (mod p). We show that a is a quadratic residue by finding a square root b modulo p.
Let g be a primitive root of p. Choose k so that a ≡ gk (mod p), and let ℓ = (p - 1)k∕2. Then
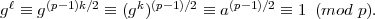
Because g is a primitive root, gℓ ≡ 1 (mod p) implies that ℓ is a multiple of p - 1. Hence, (p - 1) ∣ (p - 1)k∕2, from which we conclude that 2∣k and k∕2 is an integer. Let b = gk∕2. Then b2 ≡ gk ≡ a (mod p), so b is a square root of a modulo p, as desired. __
The Euler criterion lets us test membership in QRp for prime p, but it doesn’t tell us how to find square roots. In case p ≡ 3 (mod 4), there is an easy algorithm for finding the square roots of any member of QRp.
Claim 3 Let p ≡ 3 (mod 4), a  QRp. Then b = a(p+1)∕4 is a square root of a (mod p).
QRp. Then b = a(p+1)∕4 is a square root of a (mod p).
Proof: Under the assumptions of the claim, p + 1 is divisible by 4, so (p + 1)∕4 is an integer. Then
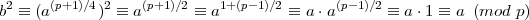
by the Euler Criterion (Claim 2). __
Let p be an odd prime. It can be written uniquely as p = 2nq + 1, where n and q are integers and q is odd. (Note that n is simply the number of trailing 0’s in the binary expansion of p, and q is what results when p is shifted right by n places.) Because p is odd, p - 1 is even, so n ≥ 1. Section 64 treats the special case where n = 1. We now present an algorithm due to D. Shanks2 that works for all n.
Let p,n,q be as above. Assume a is a quadratic residue and u is a quadratic non-residue modulo p. (We can easily find u by choosing random elements of Z*p and applying the Euler Criterion.) The goal is to find x such that x2 ≡ a (mod p).
| Shank’s Algorithm |
Input: Odd prime p, quadratic residue a  QRp. QRp. |
| Output: A square root of a (mod p). |
| 1. | Let n, q satisfy p = 2nq and q odd. |
| 2. | Let u be a quadratic non-residue modulo p. |
| 3. | k = n |
| 4. | z = uq |
| 5. | x = a(q+1)∕2 |
| 6. | b = aq |
| 7. | while (b ⁄≡ 1 (mod p)) { |
| 8. | let m be the least integer with b2m ≡ 1 (mod p) |
| 9. | t = z2k-m-1 |
| 10. | z = t2 |
| 11. | b = bz |
| 12. | x = xt |
| 13. | k = m |
| 14. | } |
| 15. | return x |
The congruence x2 ≡ ab (mod p) is easily shown to be a loop invariant. Hence, if the program terminates, x is a square root of a.
To see why it terminates after at most n iterations of the loop, we look at the orders3 of b and z (mod p) at the start of each loop iteration (before line 8) and show that ord(b) < ord(z) = 2k.
On the first iteration, k = n, z = uq, and ord(z) = 2n. Clearly
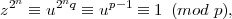
so ord(z)∣2n. By the Euler Criterion, since u is a non-residue, we have
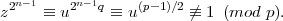
Hence, ord(z) = 2n. Using similar reasoning, since a is a quadratic residue, b2n-1 ≡ 1 (mod p), so ord(b)∣2n-1. It follows that ord(b) < ord(z) = 2n (mod p).
Now, on each iteration, line 8 sets m = ord(b) and line 9 sets t = z2k-m-1 , so
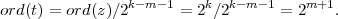
Line 10 sets z = t2, so ord(z) = ord(t)∕2 = 2m. After line 11, ord(b) < 2m. This because the old value of b and the new value of z both have order 2m. Hence, both of those numbers raised to the power 2m-1 are -1, so their product (the new value of b) raised to that same power is (-1)2 = 1. Line 13 sets k = m in preparation for the next iteration, and the loop invariant ord(b) < ord(z) = 2k is maintained. Moreover, ord(b) is reduced at each iteration, so the loop must terminate after at most n iterations.
Let n = pq, p, q distinct odd primes. We can divide the numbers in Z*n into four classes depending on their membership
in QRp and QRq.4
Let Qn11 be those numbers that are quadratic residues mod both p and q; let Qn10 be those numbers that
are quadratic residues mod p but not mod q; let Qn01 be those numbers that are quadratic residues mod q
but not mod p; and let Qn00 be those numbers that are neither quadratic residues mod p nor mod q. Under
these definitions, Qn11 = QRn and Qn00 ∪ Qn01 ∪ Qn10 = QNRn.
Fact Given a  Qn00 ∪Qn11, there is no known feasible algorithm for determining whether or not
a
Qn00 ∪Qn11, there is no known feasible algorithm for determining whether or not
a  QRn that gives the correct answer significantly more than 1/2 the time.
QRn that gives the correct answer significantly more than 1/2 the time.
The Goldwasser-Micali cryptosystem is based on this fact. The public key consist of a pair e = (n,y),
where n = pq for distinct odd primes p, q, and y  Qn00. The private key consists of p. The message space
is
Qn00. The private key consists of p. The message space
is 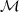 = {0,1}.
= {0,1}.
To encrypt m 
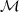 , Alice chooses a random a
, Alice chooses a random a  QRn. She does this by choosing a random member of
Z*n and squaring it. If m = 0, then c = a mod n. If m = 1, then c = ay mod n. The ciphertext is
c.
QRn. She does this by choosing a random member of
Z*n and squaring it. If m = 0, then c = a mod n. If m = 1, then c = ay mod n. The ciphertext is
c.
It is easily shown that if m = 0, then c  Qn11, and if m = 1, then c
Qn11, and if m = 1, then c  Qn00. One can also show
that every a
Qn00. One can also show
that every a  Qn11 is equally likely to be chosen as the ciphertext in case m = 0, and every
a
Qn11 is equally likely to be chosen as the ciphertext in case m = 0, and every
a  Qn00 is equally likely to be chosen as the ciphertext in case m = 1. Eve’s problem of
determining whether c encrypts 0 or 1 is the same as the problem of distinguishing between
membership in Qn00 and Qn11, which by the above fact is believed to be hard. Anyone knowing the
private key p, however, can use the Euler Criterion to quickly determine whether or not c is
a quadratic residue mod p and hence whether c
Qn00 is equally likely to be chosen as the ciphertext in case m = 1. Eve’s problem of
determining whether c encrypts 0 or 1 is the same as the problem of distinguishing between
membership in Qn00 and Qn11, which by the above fact is believed to be hard. Anyone knowing the
private key p, however, can use the Euler Criterion to quickly determine whether or not c is
a quadratic residue mod p and hence whether c  Qn11 or c
Qn11 or c  Qn00, thereby determining
m.
Qn00, thereby determining
m.
Let p be an odd prime, a an integer. The Legendre symbol  is a number in {-1,0,+1}, defined as
follows:
is a number in {-1,0,+1}, defined as
follows:
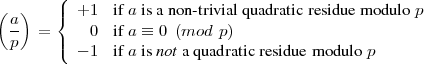
By the Euler Criterion (see Claim 2), we have
Note that this theorem holds even when p∣a.
The Legendre symbol satisfies the following multiplicative property: Fact Let p be an odd prime. Then
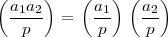
Not surprisingly, if a1 and a2 are both non-trivial quadratic residues, then so is a1a2. This shows that the fact is true for the case that
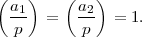
More surprising is the case when neither a1 nor a2 are quadratic residues, so
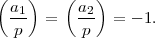
In this case, the above fact says that the product a1a2 is a quadratic residue since
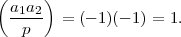
Here’s a way to see this. Let g be a primitive root of p. Write a1 ≡ gk1 (mod p) and a2 ≡ gk2 (mod p). Since a1 and a2 are not quadratic residues, it must be the case that k1 and k2 are both odd; otherwise gk1∕2 would be a square root of a1, or gk2∕2 would be a square root of a2. But then k1 + k2 is even since the sum of any two odd numbers is always even. Hence, g(k1+k2)∕2 is a square root of a1a2 ≡ gk1+k2 (mod p), so a1a2 is a quadratic residue.