YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Notes 15 (rev. 1) | |
| Professor M. J. Fischer | October 31, 2006 | |
Lecture Notes 15
One often wants to encrypt messages for privacy and sign them for integrity and authenticity. Suppose Alice has a cryptosystem (E,D) and a signature system (S,V ). Three possibilities come to mind for encrypting and signing a message m:
Note that method 3 is quite problematic since signature functions make no guarantee of privacy. In particular, if (S,V ) is, say, an RSA signature scheme, we can define a new signature scheme (S′,V ′):
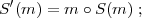
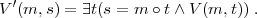
Clearly, the ability to forge signatures in (S′,V ′) implies the ability to forge signatures in (S,V ), for if (m,s) is a valid signed message in (S′,V ′), then (m,t) is a valid signed message in (S,V ), where t is the second component of the ordered pair encoded by s. Thus, the new scheme is at least as secure as the original. But with (S′,V ′), the plaintext message is part of the signature itself, so if (S′,V ′) is used as the signature scheme in method 3 above, there is no privacy.
Think about the pros and cons of the other two possibilities.
The ElGamal signature scheme uses ideas similar to those of his encryption system, which we have already seen. The private signing key consists of a primitive root g of a prime p and an exponent x. The public verification key consists of g, p, and the number a = gx mod p. The signing and verification algorithms are given below:
| To sign m:
| |
| 1. | Choose random y  Z*
φ(p). 1 Z*
φ(p). 1 |
| 2. | Compute b = gy mod p. |
| 3. | Compute c = (m - xb)y-1 mod φ(p). |
| 4. | Output signature s = (b,c). |
| To verify (m,s), where s = (b,c):
| |
| 1. | Check that abbc ≡ gm (mod p). |
Why does this work? Plugging in for a and b, we see that
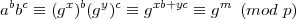
since xb + yc ≡ m (mod φ(p)).
The commonly-used Digital Signature Algorithm (DSA) is a variant of ElGamal signatures. Also called the Digital Signature Standard (DSS), it is described in U.S. Federal Information Processing Standard FIPS 186–2.2 It uses two primes: p, which is 1024 bits long,3 and q, which is 160 bits long and satisfies q∣(p - 1). Here’s how to find them: Choose q first, then search for z such that zq + 1 is prime and of the right length. Choose p = zq + 1 for such a z.
Now let g = h(p-1)∕q mod p for any h  Z*p for which g > 1. This ensures that g
Z*p for which g > 1. This ensures that g  Z*p is a
non-trivial qth root of unity modulo p. Let x
Z*p is a
non-trivial qth root of unity modulo p. Let x  Z*q and compute a = gx mod p. The parameters p, q, and g
are common to the public and private keys. In addition, the private signing key contains x and the public
verification key contains a.
Z*q and compute a = gx mod p. The parameters p, q, and g
are common to the public and private keys. In addition, the private signing key contains x and the public
verification key contains a.
Here’s how signing and verification work:
| To sign m:
| |
| 1. | Choose random y  Z*q. Z*q. |
| 2. | Compute b = (gy mod p) mod q. |
| 3. | Compute c = (m + xb)y-1 mod q. |
| 4. | Output signature s = (b,c). |
| To verify (m,s), where s = (b,c):
| |
| 1. | Verify that b,c  Z*q; reject if not. Z*q; reject if not. |
| 2. | Compute u1 = mc-1 mod q. |
| 3. | Compute u2 = bc-1 mod q. |
| 4. | Compute v = (gu1au2 mod p) mod q. |
| 5. | Check v = b. |
To see why this works, note that since gq ≡ 1 (mod p), then
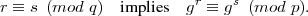
This follows from the fact that g is a qth root of unity modulo p, so gr+uq ≡ gr(gq)u ≡ gr (mod p) for any u. Hence,
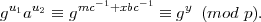
It follows that
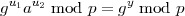
and hence
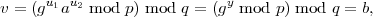
as desired. (Notice the shift between equivalence modulo p and equality of remainders modulo p.)
DSA introduces this new element of computing a number modulo p and then modulo q. Call this function fp,q(n) = (n mod p) mod q. This is not the same as n mod r for any number r, nor is it the same as (n mod q) mod p.
To understand better what’s going on, let’s look at an example. Take p = 29 and q = 7. Then 7∣(29 - 1), so this is a valid DSA prime pair. The table below lists the first 29 values of y = f29,7(n):
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| y | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 |
The sequence of function values repeats after this point with a period of length 29. Note that it both begins and ends with 0, so there is a double 0 every 29 values. That behavior cannot occur modulo any number r. That behavior is also different from f7,29(n), which is equal to n mod 7 and has period 7. (Why?)
Many cryptographic hash functions are currently in use. For example, the openssl library includes implementations of MD2, MD4, MD5, MDC2, RIPEMD, SHA, SHA–1, SHA–256, SHA–384, and SHA–512. The SHA–xxx methods are recommended for new applications, but these other functions are also in widespread use.
The revised Secure Hash Algorithm (SHA–1) is one of four algorithms described in U. S. Federal Information Processing Standard FIPS PUB 180–2 (Secure Hash Standard).4 It states,
“Secure hash algorithms are typically used with other cryptographic algorithms, such as digital signature algorithms and keyed-hash message authentication codes, or in the generation of random numbers (bits).”
SHA–1 produces a 160-bit message digest. The other algorithms in the SHA–xxx family produce longer message digests.
MD5 is an older algorithm (1992) devised by Rivest. We present an overview of it here. It generates a 128-bit message digest from an input message of any length. It is built from a basic block function g : 128-bit × 512-bit → 128-bit.
The MD5 hash function h is obtained as follows: First the original message is padded to length a multiple of 512. The result m is split into a sequence of 512-bit blocks m1,m2,…,mk. Finally, h is computed by chaining g on the first argument.
We look at these steps in greater detail. As with block encryption, it is important that the padding function be one-to-one, but for a different reason. For encryption, the one-to-one property is what allows unique decryption. For a hash function, it prevents there from being trivial colliding pairs. For example, if the last partial block is simply padded with 0’s, then all prefixes of the last message block will become the same after padding and will therefore collide with each other.
The function h can be regarded as a state machine, where the states are 128-bit strings and the inputs to the machine are 512-bit blocks. The machine starts in state s0, specified by an initialization vector IV. Each input block mi takes the machine from state si-1 to new state si = g(si-1,mi). The last state sk is the output of h, that is,
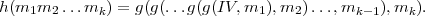
The basic block function g(s,b) consists of 4 stages, each consisting of 16 substages. Recall that b is 512-bits long, so we may divide b into 32-bit words b1b2…b16. At stage i, substage j, a permutation πi of {1,…,16} is used to select word bℓ, where ℓ = πi(j). A new state is generated by computing fi,j(s,bℓ), where s is the old state and fi,j is a bit-scrambling function that depends on i and j. Since a state can be represented by four 32-bit words, the arguments to fi,j occupy only 5 machine words, which easily fit into the high-speed registers of modern processors.