YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 467a: Cryptography and Computer Security | Notes 16 (rev. 1) |
| Professor M. J. Fischer | | November 2, 2006 |
|
|
|
| |
78 Doubling Reduction Amount of Hash Functions
Suppose we are given a particular fixed-length hash function h : 256-bits → 128-bits. How can we use h to
compute a 128-bit strong collision-free hash of a 512-bit input block? We consider several
possible ways to extend h to a hash function H : 512-bits → 128-bits. In the following, we
suppose that m is 512-bits long, and we write m = m1m2, where m1 and m2 are 256 bits
each.
-
Method 1
- Define H(m) = H(m1m2) = h(m1) ⊕ h(m2). Unfortunately, this fails to be either
strong or weak collision-free since m′ = m2m1 always collides with m under H (except in
the special case that m1 = m2.
-
Method 2
- Define H(m) = H(m1m2) = h(h(m1)h(m2)).
Theorem 1 The H of method 2 is strong collision-free assuming that the h from which it is
derived is strong collision-free.
Proof: Assume the contrary, that one can find a colliding pair (m,m′) for H. We show
that one can then find a colliding pair for h, contradicting the assumption that h is strong
collision-free.
Write m = m1m2 and m′ = m′1m′2 for 256-bit blocks m1,m2,m′1,m′2. Since m collides
with m′, we have that m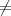 m′ but H(m) = H(m′). We consider two cases.
m′ but H(m) = H(m′). We consider two cases.
Case 1: h(m1) h(m′1) or h(m2)
h(m′1) or h(m2) h(m′2). Let u = h(m1)h(m2) and u′ = h(m′1)h(m′2).
Then u
h(m′2). Let u = h(m1)h(m2) and u′ = h(m′1)h(m′2).
Then u u′, but h(u) = H(m) = H(m′) = h(u′), so (u,u′) is a colliding pair for h.
u′, but h(u) = H(m) = H(m′) = h(u′), so (u,u′) is a colliding pair for h.
Case 2: h(m1) = h(m′1) and h(m2) = h(m′2). Since m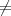 m′, then either m1
m′, then either m1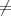 m′1 or
m2
m′1 or
m2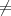 m′2 (or both). But then whichever pair is unequal is a colliding pair for h.
m′2 (or both). But then whichever pair is unequal is a colliding pair for h.
In either case, we have found a colliding pair for h, contradicting the assumption that h was
strong collision-free. __
79 A General Chaining Method for Constructing Hash Functions
Assume now that we have a hash function h : r-bits → t-bits, where r ≥ t + 2. In the above example,
r = 256 and t = 128. Divide the message m after appropriate padding into blocks m1m2…mk, each of
length r - t - 1. Compute a sequence of t-bit states as follows:

Then H(m) = sk.
Theorem 2 Let H and h be the functions of section 79. Then H is strong collision-free assuming
that h is.
Proof: Assume to the contrary that H is not strong collision-free, so we are able to find a colliding
pair (m,m′) for H. We show how to find a colliding pair for h, contradicting the assumed
collision-freedom of h.
Let m = m1m2…mk, let m′ = m′1m′2…m′k′, and let s1,…,sk and s′1,…,s′k′ be the
corresponding state sequences. We may assume without loss of generality that k ≤ k′. Because m
and m′ collide under H, we have sk = s′k′. Let i be the least integer in {1,…,k} such that, for all
j  {i,…,k}, we have sj = s′k′-k+j. Such an i exists since i = k is one value that works. We
proceed by cases:
{i,…,k}, we have sj = s′k′-k+j. Such an i exists since i = k is one value that works. We
proceed by cases:
Case 1: i = 1 and k = k′. Then sj = s′j for all j = 1,…,k. Because m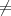 m′, there must be
some ℓ such that mℓ
m′, there must be
some ℓ such that mℓ m′ℓ. If ℓ = 1, then (0t0m1,0t0m′1) is a colliding pair for h. If ℓ > 1, then
(sℓ-11mℓ, s′ℓ-11m′ℓ) is a colliding pair for h.
m′ℓ. If ℓ = 1, then (0t0m1,0t0m′1) is a colliding pair for h. If ℓ > 1, then
(sℓ-11mℓ, s′ℓ-11m′ℓ) is a colliding pair for h.
Case 2: i = 1 and k < k′. Let u = k′- k + 1. Then s1 = s′u. Since u > 1 we have that
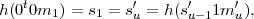
so (0t0m1, s′u-11m′u) is a colliding pair for h. Note that this is true even if 0t = s′u-1 and
m1 = m′u, a possibility that we have not ruled out.
Case 3: i > 1. Then u = k′-k +i > 1. By the definition of i, we have si = s′u, but si-1 s′u-1
since i was chosen to be as small as possible. Hence,
s′u-1
since i was chosen to be as small as possible. Hence,

so (si-11mi, s′u-11m′u) is a colliding pair for h.
In each case, we have found a colliding pair for h. The contradicts the assumption that h is
strong collision-free. Hence, H is also strong collision-free. __
80 Hash Functions Do Not Always Look Random
Intuitively, we like to think of h(y) as being “random-looking”, with no obvious pattern. Indeed, it would
seem that obvious patterns and structure in h would provide a means of finding collisions, violating the
property of being strong-collision free. But this intuition is faulty, as I now show.
Suppose h is a strong collision-free hash function. Define H(x) = 0 ⋅ h(x). Clearly, H also enjoys
these same properties. If (x1,x2) is a colliding pair for H, then it is also a colliding pair for h. Thus, H is
strong collision-free, despite the fact that the string H(x) always begins with 0. Later on, we will
talk about how to make functions that truly do appear to be random (even though they are
not).
81 Birthday Attack on Hash Functions
Recall that the MD5 hash function produces 128-bit values, whereas SDA–1 produces 160-bit values. How
many bits do we need for security? Both 2128 and 2160 are more than large enough to thwart a brute force
attack that simply searches randomly for colliding pairs (m,m′). However, the so-called Birthday Attack
reduces the size of the search space to roughly the square root of the original size. Thus, MD5 has roughly
the same resistance to the birthday attack as a cryptosystem with 64-bit keys would have to a brute
force attack. Similarly, SHA–1’s effective size in terms of birthday attack resistance is only
80-bits.
We saw an example of a birthday attack in section 26.1 of lecture notes 5. The birthday attack is
named for the birthday paradox. This is the fact that there is approximately a 50–50 chance that two people
in a room of 23 strangers have the same birthday. There is a nice description of the birthday paradox on the
web at http://en.wikipedia.org/wiki/Birthday_paradox. The probability of not having two people with the
same birthday is is

Hence, the probability that (at least) two people have the same birthday is 1 - q = 0.507297. This
probability grows quite rapidly with the number of people in the room. For example, with 46 people, the
probability that two share a birthday is 0.948253.
The birthday paradox can be applied to hash functions to yield a much faster way to find colliding pairs
than choosing pairs at random. The idea is to choose a random set of k messages and then see if any two
messages in the set collide. There are (k
2)
= k(k - 1)∕2 different pairs of messages in a set of size k,
so on can test this many pairs at a cost of only k evaluations of the hash function. Of course,
these (k
2)
pairs are not uniformly distributed, so one needs a birthday-paradox style analysis of
the probability that a colliding pair will be found. The general result is that the probability of
success is at least one half for k roughly the size of 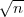 , where n is the size of the message
space.
, where n is the size of the message
space.
Two problems remain that make this attack difficult to use in practice. First, there is the problem of
finding duplicates in the list of hash values. That can be done in time O(k log k) by sorting the list and
then looking for adjacent equal elements. The more serious problem with this approach, and
with the birthday attack in general, is the amount of storage required. While carrying out 264
computational steps is almost on the verge of feasibility, finding that much storage is still way
out of the question, so MD5 and other 128-bit hash functions are still safe from this attack.
Nevertheless, the birthday attack is one of the more subtle ways that cryptographic primitives can be
compromised.
82 Hash from Cryptosystem
We’ve already seen several cryptographic hash functions as well as methods for making new hash functions
from old. Here’s a way to make a hash function from a symmetric cryptosystem with encryption function
Ek(b). Assume that the key length and block length are the same. Let m be an arbitrary length message.
Pad it appropriately and divide it into block lengths appropriate for the cryptosystem. Compute the
following state sequence:

The output H(m) of the new hash function is sk. IV is an initial vector and f is a function built from E.
Some possibilities for f are
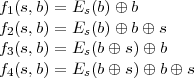
You should think about why these particular functions do or do not lead to a strong collision-free hash
function. For example, if k = 1 and f = f1, then H1(b) = EIV (b) ⊕b. EIV itself is one-to-one (since it’s
an encryption function), but what can we say about H1(b)? Indeed, if bad luck would have it
that EIV is the identity function, then H1(b) = 0 for all b, and all pairs of message blocks
collide!
83 Authentication Problem
The authentication problem is to identify who one is communicating with. For example, if Alice and Bob
are communicating over a network, then Bob would like to know that he is talking to Alice and not to
someone else on the network. Knowing the IP address or URL is not adequate since Mallory might be in
control of intermediate routers and name servers.
As with signature schemes, we need some way to differentiate the real Alice from other users of the
network. We generally do this by assuming that Alice possess some secret or password that is not
known to anyone else. Then Alice authenticates herself by proving that she knows the secret
password.
84 Passwords
Password mechanisms are widely used for authentication. In the usual form, Alice authenticates herself by
sending her password to Bob. Bob checks that it matches Alice’s password and grants access. This is the
scheme that is used for local logins to a computer and is also used for remote authenticated telnet, ftp, rsh,
and rlogin sessions. Such schemes have two major security weaknesses:
- Except for local logins, the password is sent over the network in the clear. This exposes it to
various kinds of eavesdropping, ranging from ethernet packet sniffers on the LAN to corrupt
ISP’s and routers along the way. The real threat of password capture in this way is so great
that it is highly recommended that one never send a password over the internet in the clear.
Users of the old insecure Unix tools should switch to secure replacements such as ssh, slogin,
and scp, or kerberized versions of telnet and ftp.
Logins into web sites often use the SSL (Secure Socket Layer) protocol to encrypt the
connection, making it safe to transmit passwords to the site, but some do not. Depending
on how you have it configured, your browser will warn you whenever you attempt to send
unencrypted data back to the server.
- Even if the password reaches the server safely, it is no longer the case that Alice is the only
one who knows her password. Now the server also knows. This is no problem if the only
use of the password is to authenticate Alice to that particular server, but what it means is
that from then on, the server can impersonate Alice to any other service that uses the same
password.
Users these days may have accounts with dozens of different web sites. In order make the
task of remembering the user names and passwords on all those sites, one is tempted to use
the same user name-password pairs on all of them. But that means that anyone with access
to the password database on one site could log into Alice’s account on any of the other sites.
Typically the different sites have very differing sensitivity of the data they protect. An on-line
shopping site may only be protecting a customer’s shopping cart, whereas a banking site
allows access to a customer’s bank account.
My advice is to use a different password for each account. Of course, nobody can keep dozens
of different passwords straight, so the downside of my suggestion is that the passwords must
be written down and kept safe. If the primary paper on which they are written gets lost, then
one should have a backup copy so that one can go to all of the sites ASAP and change the
passwords (and learn if the site has been compromised).
The real problem with simple password schemes is that Alice is required to send her secrets to other
parties in order to use them. We will see in the next lecture authentication schemes that do not require
this.
85 Secure Password Storage
Another issue with traditional password authentication schemes is the necessity of storing the
passwords on the server for later verification. The file in which the passwords are stored is
obviously highly sensitive. While operating system protections can (and should) be used to
protect it, they are not really sufficient. For one thing, legitimate sysadmins can access it and
might conceivably use the passwords found there to log into users’ accounts at other sites.
Hackers who manage to break into the computer and obtain root privileges could also do the
same thing. Finally, files get copied onto backup tapes that are not subject to the same system
protections, so someone with access to a backup tape could read everybody’s password from
it.
Rather than store passwords in the clear, it is usual to store “encrypted” passwords, which really means
the hash value of the password under some cryptographic hash function. The authentication function takes
the cleartext password from the user, computes its hash value, and sees if that matches the hashed value in
the password file. Since the password does not contain the actual password, and it is computationally
difficult to invert a cryptographic hash function, knowledge of the hash value does not allow an attacker to
easily find the password.
86 Dictionary Attacks
Nevertheless, access to the password file, even if only hashed passwords are stored, opens up the possibility
of a dictionary attack. The idea here is that many users choose weak passwords—words that appear in
an English dictionary or in other available sources of text. If one has access to the password
hashes of legitimate users on the computer (such as is contained in /etc/passwd on Unix), an
attacker can hash every word in the dictionary and then look for matches with the password file
entries. This attack is quite likely to succeed in compromising at least a few accounts on a typical
system. Even one compromised account is enough to allow the hacker to log into the system as a
legitimate user, from which other kinds of attacks are possible that cannot be carried out from the
outside.
A way to make dictionary attacks more expensive is to add salt to each password. Salt is a
random number that is attached to a user’s account and stored along with the user name and
hashed password in the password file. The hash function takes two arguments, the password and
salt, and produces a hash value. Because the salt is stored (in the clear) in the password file,
the user’s password can be easily verified. However, a particular password hashes in different
ways depending on the salt value. This means that a successful dictionary attack would have to
encrypt the entire dictionary with every possible salt value (or at least with every salt value that
appeared in the password file being attacked). This increases the cost of the attack by orders of
magnitude.
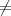 m′ but H(m) = H(m′). We consider two cases.
m′ but H(m) = H(m′). We consider two cases.
 h(m′1) or h(m2)
h(m′1) or h(m2) h(m′2). Let u = h(m1)h(m2) and u′ = h(m′1)h(m′2).
Then u
h(m′2). Let u = h(m1)h(m2) and u′ = h(m′1)h(m′2).
Then u u′, but h(u) = H(m) = H(m′) = h(u′), so (u,u′) is a colliding pair for h.
u′, but h(u) = H(m) = H(m′) = h(u′), so (u,u′) is a colliding pair for h.
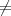 m′, then either m1
m′, then either m1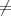 m′1 or
m2
m′1 or
m2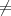 m′2 (or both). But then whichever pair is unequal is a colliding pair for h.
m′2 (or both). But then whichever pair is unequal is a colliding pair for h.

 {
{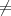

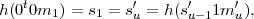



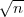 , where
, where