YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Notes 21 (rev. 1) | |
| Professor M. J. Fischer | November 28, 2006 | |
Lecture Notes 21
A pseudorandom sequence generator (PRSG) maps a “short” random seed to a “long” pseudorandom bit string. For a PRSG to be cryptographically strong, it must be difficult to correctly predict any generated bit, even knowing all of the other bits of the output sequence. In particular, it must also be difficult to find the seed given the output sequence, since if one knows the seed, then the whole sequence can be generated. Thus, a PRSG is a one-way function and more. While a hash function might generate hash values of the form yy and still be strongly collision-free, such a function could not be a PRSG since it would be possible to predict the second half of the output knowing the first half.
I am being intentionally vague at this stage about what “short” and “long” mean, but intuitively, “short” is a length like we use for cryptographic keys—long enough to prevent brute-force attacks, but generally much shorter than the data we want to deal with. Think of “short”=128 or =256 and you’ll be in the right ballpark. By “long”, we mean much larger sizes, perhaps thousands or even millions of bits. In practice, we usually thing of the output length as being variable, so that we can request as many output bits from the generator as we like and it will deliver them. Also, in practice, the bits are generally delivered a block at a time rather than all at once, so we don’t even need to announce in advance how many bits we want but can go back as needed to get more.
There are many ways to use a PRSG G for bit commitment. One such way is shown in Figure 1. Here, ρ is a security parameter that controls the probability that a cheating Alice can fool Bob. We let Gρ(s) denote the first ρ bits of G(s).
Assuming G is cryptographically strong, then c will look random to Bob, regardless of the value of b, so he will be unable to get any information about b.
The purpose of r is to protect Bob against a cheating Alice. Alice can cheat if she can find a triple (c,s0,s1) such that s0 opens c to reveal 0 and s1 opens c to reveal 1. Such a triple must satisfy the following pair of equations:
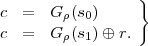 | (1) |
It is sufficient for her to solve the equation
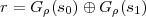 | (2) |
for s0 and s1 and then choose c = Gρ(s0).
One might ask why Bob needs to choose r? Why can’t Alice choose r, or why can’t r be fixed to some constant? If Alice chooses r, then she can easily solve (2) and cheat. If r is fixed to a constant, then if Alice ever finds a triple (c,s0,s1) satisfying (1), she can fool Bob every time. While finding such a pair would be difficult if Gρ were a truly random function, any specific PRSG might have special properties, at least for a few seeds, that would make this possible. For example, suppose r = 1ρ and Gρ(¬s0) = ¬Gρ(s0) for some s0. Then (2) could be solved by taking s1 = ¬s0. By having Bob choose r at random, r will be different each time (with very high probability), and a successful cheating Alice would be forced to solve (1) in general, not just for one special case.
The three bit-commitment protocols of the previous section all have the same form. We abstract from these
protocols a cryptographic primitive, called a bit-commitment scheme, which consists of a pair of key spaces

 and
and 
 , a blob space
, a blob space  , a commitment function
, a commitment function
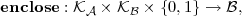
and an opening function
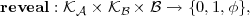
where φ means “failure”. We say that a blob c 
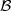 contains b
contains b  {0,1} if reveal(kA,kB,c) = b for some
kA
{0,1} if reveal(kA,kB,c) = b for some
kA 
 A and kB
A and kB 
 B.
B.
These functions have three properties:

 A,∀kB
A,∀kB 
 B,∀b
B,∀b  {0,1}, reveal(kA,kB,enclose(kA,kB,b)) = b;
{0,1}, reveal(kA,kB,enclose(kA,kB,b)) = b;

 B,∀c
B,∀c 
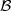 ,∃b
,∃b  {0,1},∀kA
{0,1},∀kA 
 A, reveal(kA,kB,c)
A, reveal(kA,kB,c)  {b,φ}.
{b,φ}.
The intention is that kA is chosen by Alice and kB by Bob. Intuitively, these conditions say:
A bit-commitment scheme looks a lot like a symmetric cryptosystem, with enclose(kA,kB,b) playing the role of the encryption function and reveal(kA,kB,c) the role of the decryption function. However, they differ both in their properties and in the environments in which they are used. Conventional cryptosystems do not require condition 2, nor do they necessarily satisfy it. In a conventional cryptosystem, it is assumed that Alice and Bob trust each other and both share a secret key k. The cryptosystem is designed to protect Alice’s secret message from a passive eavesdropper Eve. In a bit-commitment scheme, Alice and Bob cooperate in the protocol but do not trust each other to choose the key. Rather, the key is split into two pieces, kA and kB, with each participant controlling one piece.
A bit-commitment scheme can be turned into a bit-commitment protocol by plugging it into the generic protocol given in Figure 2.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
Each of the bit-commitment protocols of sections 103 and 104 (lecture notes 20), and section 105
above can be regarded as an instance of the generic protocol. For example, we get the protocol of
Figure 1 in section 103 (lecture notes 20) by taking 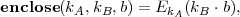 and
and

Alice and Bob are in the process of getting divorced and are trying to decide who gets custody of their pet cat, Fluffy. They both want the cat, so they agree to decide by flipping a coin: heads Alice wins; tails Bob wins. Bob has already moved out and does not wish to be in the same room with Alice. The feeling is mutual, so Alice proposes that she flip the coin and telephone Bob with the result.
This proposal of course is not acceptable to Bob since he has no way of knowing whether Alice is telling the truth when she says that the coin landed heads. “Look Alice,” he says, “to be fair, we both have to be involved in flipping the coin. We’ll each flip a private coin and XOR our two coins together to determine who gets Fluffy. You should be happy with this arrangement since even if you don’t trust me to flip fairly, your own fair coin is sufficient to ensure that the XOR is unbiased.” This sounds reasonable to Alice, so she lets him go on to propose the protocol of Figure 3. In this protocol, 1 means “heads” and 0 means “tails”.
|
|
After Alice considers Figure 3 for awhile, she objects. “This isn’t fair. You get to see my coin flip before I see yours, so now you have complete control over the value of b.” She suggests that she would be happy if the first two steps were reversed, so that Bob flipped his coin first, but Bob balks at that suggestion.
They then both remember last week’s lecture and decide to use blobs to prevent either party from controlling the outcome. They agree on the protocol of Figure 4. At the completion of step 2, both Alice and Bob have each other’s commitment (something they failed to achieve in the past, which is why they’re in the middle of a divorce now), but neither know the other’s private bit. They each learn each other’s bit at the completion of steps 3 and 4.
|
|
While this protocol appears to be completely symmetric, it really isn’t quite, for one of the parties completes step 3 before the other one does. Say Alice receives sB before sending sA. At that point, she can compute bB and hence know the coin outcome b. If it turns out that she lost, she might decide to stop the protocol and refuse to complete her part of step 3.
We haven’t really addressed the question for any of these protocols about what happens if one party quits in the middle or one party detects the other party cheating. We have only been concerned until now with the possibility of undetected cheating. But in any real situation, one party might feel that he or she stands to gain by cheating, even if the cheating is detected. That in turn raises complicated questions as to what happens next. Does a third party Carol become involved? If so, can Bob prove to Carol that Alice cheated? What if Alice refuses to talk to Carol? It may be instructive to think about the recourse that Bob has in similar real-life situations and to consider the reasons why such situations rarely arise. For example, what happens if someone fails to follow the provisions of a contract or if someone ignores a summons to appear in court?
There is another subtle problem with the protocol of Figure 4. Suppose that Bob sends his message before Alice sends hers in each of steps 1, 2, and 3. Then Alice can choose kA = kB, cA = cB, and sA = sB rather than following her proper protocol. In step 4, Bob will compute

so he won’t detect that anything is wrong, and the coin outcome is b = bA ⊕ bB = bA ⊕ bA = 0. Hence, Alice can force the outcome to be 0 simply by playing copycat.
This problem is not so easy to overcome. One possibility is for both Alice and Bob to check after
step 1 that kA kB. That way, if Alice, say, plays copycat on steps 2 and 3, there is a good chance
that
kB. That way, if Alice, say, plays copycat on steps 2 and 3, there is a good chance
that

However, depending on the bit commitment scheme, a difference in only one bit in kA and kB might not be enough to ensure that different bits are revealed.
A better idea might be to both check that kA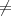 kB after step 1 and then to use h(kA) and h(kB) in
place of kA and kB, respectively, in the remainder of the protocol, where h is a hash function. That way,
even a single bit difference in kA and kB is likely to be magnified to a large difference in the strings h(kA)
and h(kB). This should lead to the bits reveal(sA,h(kB),cA) and reveal(sB,h(kA),cB) being
uncorrelated, even if sA = sB and cA = cB.
kB after step 1 and then to use h(kA) and h(kB) in
place of kA and kB, respectively, in the remainder of the protocol, where h is a hash function. That way,
even a single bit difference in kA and kB is likely to be magnified to a large difference in the strings h(kA)
and h(kB). This should lead to the bits reveal(sA,h(kB),cA) and reveal(sB,h(kA),cB) being
uncorrelated, even if sA = sB and cA = cB.
Protocols for coin flipping and for dealing a poker hand from a deck of cards can be based on the intuitive notion of locked boxes. This idea in turn can be implemented using commutative cryptosystems.
We discussed the coin-flipping problem in section 107 and presented a protocol based on bit-commitment. Here we present a coin-flipping protocol based on the idea of locked boxes.
Alice and Bob can carry out this protocol electronically using any commutative cryptosystem, that is, one in which EA(EB(m)) = EB(EA(m)) for all messages m. RSA is commutative for keys with a common modulus n, so we can use RSA in an unconventional way. Rather than making the encryption exponent public and keeping the factorization of n private, we turn things around. Alice and Bob jointly chose primes p and q, and both compute n = pq. Alice then chooses an RSA key pair A = ((eA,n),(dA,n)), which she can do since she knows the factorization of n. Similarly, Bob chooses an RSA key pair B = ((eB,n),(dB,n)) using the same n. Alice and Bob both keep their key pairs private (until the end of the protocol, when they reveal them to each other to verify that there was no cheating).
We note that this scheme may have completely different security properties from usual RSA. In RSA, there are three different secrets involved with the key: the factorization of n, the encryption exponent e, and the decryption exponent d. We have seen previously that knowing n and any two of these pieces of information allows the third to be reconstructed. Thus, knowing the factorization of n and e lets one compute d (easy). We also showed in section 55.3 ((lecture notes 10) how to factor n given both e and d.
The way RSA is usually used, only e is public, and it is believed to be hard to find the other quantities. Here we propose making the factorization of n public but keeping e and d private. It may indeed be hard to find e and d, even knowing the factorization of n, but if it is, that fact is not going to follow from the difficulty of factoring n. Of course, for security, we need more than just that it is hard to find e and d. We also need it to be hard to find m given c = me mod n. This is reminiscent of the discrete log problem, but of course n is not prime in this case.
Assuming RSA used in this new way is secure, we can implement the locked box protocol as shown in Figure 5. Here we assume that Alice and Bob initially know large primes p and q. In step (2), Alice chooses a random number r such that r < (n - 1)∕2. This ensures that m0 and m1 are both in Zn. Note that i and r can be efficiently recovered from mi since i is just the low-order bit of mi and r = (mi - i)∕2.
|
|
To see that the protocol works when both Alice and Bob are honest, observe that in step 3, cab = EB(EA(mj)) for some j. Then in step 4, cb = DA(EB(EA(mj))) = EB(mj) by the commutativity of EA and EB. Hence, in step 5, m = mj is one of Alice’s strings from step 2.
A dishonest Bob can control the outcome of the coin toss if he can find two keys B and B′ such that EB(ca) = EB′(c′a), where C = {ca,c′a} is the set received from Alice in step 2. In this case, cab = EB(EA(mj)) = EB′(EA(m1-j)) for some j. Then in step 4, cb = EB(mj) = EB′(m1-j). Hence, mj = DB(cb) and m1-j = DB′(cb), so Bob can obtain both of Alice’s messages and then send B or B′ in step 5 to force the outcome to be as he pleases.
The same locked box paradigm can be used for dealing a 5-card poker hand from a deck of cards. Alice takes a deck of cards, places each card in a separate box, and locks each box with her lock. She arranges the boxes in random order and ships them off to Bob. Bob picks five boxes, locks each with his lock, and send them back. Alice removes her locks from those five boxes and returns them to Bob. Bob unlocks them and obtains the five cards of his poker hand. Further details are left to the reader.