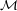 =
= 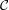 =
=  = X = X1 ∪ X2, and let n = |X| = 26.
Define
= X = X1 ∪ X2, and let n = |X| = 26.
Define
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Handout #4 | |
| Professor M. J. Fischer | September 25, 2008 | |
Problem Set 2
Due on Friday, October 3, 2008.
In this problem set, we consider a variant of the Caesar cipher which we call the “Happy” cipher (named
after the venerable “Happy Hacker” of CPSC 223 fame). Happy (E,D) is defined as follows: Let
X1 = {0,…,12} and X2 = {13,…,25}. Let 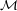 =
= 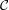 =
=  = X = X1 ∪ X2, and let n = |X| = 26.
Define
= X = X1 ∪ X2, and let n = |X| = 26.
Define
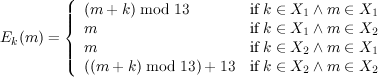
We also consider Double Happy (E2,D2). Here,  2 =
2 =  ×
× , and E(k1,k2)2 = Ek2(Ek1(m)).
, and E(k1,k2)2 = Ek2(Ek1(m)).
Problem 1: Happy Encryption (5 points)
Encrypt the plaintext “i am a secret message” using Happy with key k = 3. (As usual, we will ignore spaces.)
Problem 2: Happy Decryption (5 points)
Describe the Happy decryption function Dk(c).
Problem 3: Security (10 points)
Problem 4: Equivalent Key Pairs (10 points)
Suppose m0 = c0 = 4.
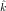 ,
,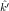 )2(m0) =
E(k,k′)2(m0) = c0, does E(
)2(m0) =
E(k,k′)2(m0) = c0, does E(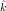 ,
,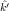 )2(m) = E(k,k′)2(m) for all m
)2(m) = E(k,k′)2(m) for all m 
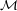 ? Why or why not?
? Why or why not?Problem 5: Group Property (10 points)
Is Happy a group? Why or why not?
___________________________________________________________________________________
The following problems ask you to compute probabilities. You may do so either analytically (if you’re facile with combinatorial counting techniques) or experimentally by writing a program to simulate 1000 random trials and reporting the fraction of times that the desired result is obtained. Either way, you should show your work – analytic derivation, or program and simulation results.
Problem 6: Birthday Problem (20 points)
Suppose u1,…,u6 and v1,…,v6 are chosen uniformly and independently at random from X
(so duplicates are possible. Find the probability that {u1,…,u6}∩{v1,…,v6}≠∅. (Note that
6 = ⌈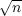 ⌉.)
⌉.)
Problem 7: Birthday Attack on Double Happy (40 points)
Assume Alice chooses a random key pair (k0,k′0) and a random message m and computes
c = E(k0,k′0)2(m) using Double Happy. Eve learns the plaintext-ciphertext pair (m,c) and then carries out
the Birthday Attack for m 
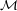 and c
and c 
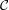 as follows:
as follows:
 and computes ui = Eki(m) for
i = 1,…,6.
and computes ui = Eki(m) for
i = 1,…,6.
 and computes vj = Dk′j(c) for
j = 1,…,6.
and computes vj = Dk′j(c) for
j = 1,…,6.

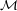 , then
we say the Birthday Attack succeeds in breaking Double Happy.
, then
we say the Birthday Attack succeeds in breaking Double Happy.