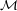 =
= 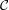 =
=  = X = X1 ∪ X2, and let n = |X| = 26.
Define
= X = X1 ∪ X2, and let n = |X| = 26.
Define
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Handout #9 | |
| Xueyuan Su | October 12, 2008 | |
Solution to Problem Set 2
In this problem set, we consider a variant of the Caesar cipher which we call the “Happy” cipher (named
after the venerable “Happy Hacker” of CPSC 223 fame). Happy (E,D) is defined as follows: Let
X1 = {0,…,12} and X2 = {13,…,25}. Let 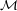 =
= 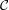 =
=  = X = X1 ∪ X2, and let n = |X| = 26.
Define
= X = X1 ∪ X2, and let n = |X| = 26.
Define
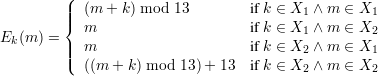
We also consider Double Happy (E2,D2). Here,  2 =
2 =  ×
× , and E(k1,k2)2 = Ek2(Ek1(m)).
, and E(k1,k2)2 = Ek2(Ek1(m)).
Problem 1: Happy Encryption (5 points)
Encrypt the plaintext “i am a secret message” using Happy with key k = 3. (As usual, we will ignore spaces.)
Solution:
m = “i am a secret message”;
k = 3;
c = “l dc d shfrht chssdjh”.
Problem 2: Happy Decryption (5 points)
Describe the Happy decryption function Dk(c).
Solution:
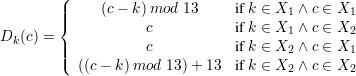 | (1) |
Problem 3: Security (10 points)
Solution:
(a) No. Before observing any cipher text, the probability of the plain text m being a specific letter m0 is
Prob[m = m0] = 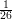 . After observing the cipher text, say c = m0, the probability of the plain text
m = m0 becomes Prob[m = m0∣c = m0] =
. After observing the cipher text, say c = m0, the probability of the plain text
m = m0 becomes Prob[m = m0∣c = m0] = 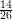 . Assuming m0 = 23, Figure 1 illustrates the plain text
prior probability distribution and posterior probability distribution after we learn the cipher text
c = m0 = 23.
. Assuming m0 = 23, Figure 1 illustrates the plain text
prior probability distribution and posterior probability distribution after we learn the cipher text
c = m0 = 23.
Problem 4: Equivalent Key Pairs (10 points)
Suppose m0 = c0 = 4.
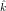 ,
,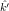 )2(m0) =
E(k,k′)2(m0) = c0, does E(
)2(m0) =
E(k,k′)2(m0) = c0, does E(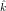 ,
,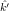 )2(m) = E(k,k′)2(m) for all m
)2(m) = E(k,k′)2(m) for all m 
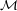 ? Why or why not?
? Why or why not?
Solution:
(a) Note that m0,k0  X1. There are four different cases:
X1. There are four different cases:
 X2}
X2}
 X2}
X2}
 X2}
X2}
 X1,(k + k′) mod13 = 0}
X1,(k + k′) mod13 = 0}(b) No. For example, if m = 13, then E13,142(13) = 14 (case 1), but E1,122(13) = 13 (case 4).
Problem 5: Group Property (10 points)
Is Happy a group? Why or why not?
Solution:
No. group property requires that for any key pairs k1,k2  X, there is always a single key k
X, there is always a single key k  X, such
that Ek1,k2(m) = Ek(m) for any m
X, such
that Ek1,k2(m) = Ek(m) for any m  X. Taking k1 = 1,k2 = 14 for example, now we will show that ∀k,
there ∃m such that Ek1,k2(m)≠Ek(m).
X. Taking k1 = 1,k2 = 14 for example, now we will show that ∀k,
there ∃m such that Ek1,k2(m)≠Ek(m).
 X1: E1,14(13) = 14, but Ek(13) = 13
X1: E1,14(13) = 14, but Ek(13) = 13
 X2: E1,14(0) = 1, but Ek(0) = 0
X2: E1,14(0) = 1, but Ek(0) = 0___________________________________________________________________________________
The following problems ask you to compute probabilities. You may do so either analytically (if you’re facile with combinatorial counting techniques) or experimentally by writing a program to simulate 1000 random trials and reporting the fraction of times that the desired result is obtained. Either way, you should show your work – analytic derivation, or program and simulation results.
Problem 6: Birthday Problem (20 points)
Suppose u1,…,u6 and v1,…,v6 are chosen uniformly and independently at random from X
(so duplicates are possible. Find the probability that {u1,…,u6}∩{v1,…,v6}≠∅. (Note that
6 = ⌈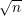 ⌉.)
⌉.)
Solution:
We first calculate the probability that sets {ui} and {vi} do not have intersection and analyze this situation case by case as follows:
1) 6 members of set {ui} are identical, (i.e., the form 6), {vi} choose from the remaining 25 letters:
![p1 = [1× (-1-)5]× [(25)6]
26 26](ho0911x.png) | (2) |
2) 5 members of set {ui} are identical, (i.e., the form 5:1), {vi} choose from the remaining 24 letters:
![( )
6 -1-4 25- 24-6
p2 = 5 × [1 × (26) × 26]× [(26) ]](ho0912x.png) | (3) |
3) 4 members of set {ui} are identical, the rest 2 members themselves are identical, (i.e., the form 4:2), {vi} choose from the remaining 24 letters:
![( )
p = 6 × [1× ( 1-)3 × 25-×-1-]× [( 24)6]
3 4 26 26 26 26](ho0913x.png) | (4) |
4) 4 members of set {ui} are identical, the rest 2 members themselves are different, (i.e., the form 4:1:1), {vi} choose from the remaining 23 letters:
![( )
p4 = 6 × [1× ( 1-)3 × 25-× 24-]× [( 23)6]
4 26 26 26 26](ho0914x.png) | (5) |
5) 3 members of set {ui} are identical, the rest 3 members themselves are identical, (i.e., the form 3:3), {vi} choose from the remaining 24 letters:
![( )
6 1 1 2 25 1 2 24 6
p5 = 3 × 2! × [1× (26) × 26-× (26-)]× [(26) ]](ho0915x.png) | (6) |
6) 3 members of set {ui} are identical, other 2 members themselves are identical, the last one is different (i.e., the form 3:2:1), {vi} choose from the remaining 23 letters:
![( ) ( )
p6 = 6 × 3 × [1× (-1-)2 × 25-× -1-× 24-]× [(23-)6]
3 2 26 26 26 26 26](ho0916x.png) | (7) |
7) 3 members of set {ui} are identical, the rest 3 members themselves are all different, (i.e., the form 3:1:1:1), {vi} choose from the remaining 22 letters:
![( )
6 1 2 25 24 23 22 6
p7 = 3 × [1 × (26) × 26-× 26-× 26]× [(26) ]](ho0917x.png) | (8) |
8) {ui} are in the form of 2:2:2, {vi} choose from the remaining 23 letters:
![(6 ) (4) 1 1 25 1 24 1 23
p8 = × × --× [1× --× --× ---× ---× --]× [(--)6]
2 2 3! 26 26 26 26 26 26](ho0918x.png) | (9) |
9) {ui} are in the form of 2:2:1:1, {vi} choose from the remaining 22 letters:
![( ) ( )
6 4 1 1 25 1 24 23 22 6
p9 = 2 × 2 × 2! × [1× 26 × 26 × 26-× 26-× 26]× [(26) ]](ho0919x.png) | (10) |
10) {ui} are in the form of 2:1:1:1:1, {vi} choose from the remaining 21 letters:
![( )
6 -1- 25- 24- 23- 22- 21-6
p10 = 2 × [1× 26 × 26 × 26 × 26 × 26]× [(26) ]](ho0920x.png) | (11) |
11) All members of {ui} are different, (i.e., the form of 1:1:1:1:1:1), {vi} choose from the remaining 20 letters:
![p11 = [1 × 25-× 24-× 23-× 22-× 21-]× [(20-)6]
26 26 26 26 26 26](ho0921x.png) | (12) |
Then the probability of non-empty intersection between ui and vi is:
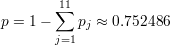 | (13) |
The above calculation is pretty tedious, but it helps to understand the detailed analysis. We can also use Monte Carlo simulation to obtain the success probabilities.
We can make use of the randRange() function we constructed in PS1 to generate a 6 random numbers ui and another 6 random numbers vi. Then we check each pair of (ui,vi) one by one to see whether there is a match. If there is such match, the counter increases by 1. In each experiment we run 1,000,000 trials and calculates the non-empty intersection probability. Then we run the experiments for 100 times and calculate the probability. The result is shown in Figure 2. The average probability is about 75.25%.
Problem 7: Birthday Attack on Double Happy (40 points)
Assume Alice chooses a random key pair (k0,k′0) and a random message m and computes
c = E(k0,k′0)2(m) using Double Happy. Eve learns the plaintext-ciphertext pair (m,c) and then carries out
the Birthday Attack for m 
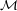 and c
and c 
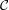 as follows:
as follows:
 and computes ui = Eki(m) for
i = 1,…,6.
and computes ui = Eki(m) for
i = 1,…,6.
 and computes vj = Dk′j(c) for
j = 1,…,6.
and computes vj = Dk′j(c) for
j = 1,…,6.

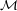 , then
we say the Birthday Attack succeeds in breaking Double Happy.
, then
we say the Birthday Attack succeeds in breaking Double Happy.
Solution:
(a) To successfully produce a candidate key pair, it means that the Birthday Attack succeeds in finding a key pair that decrypts a known plaintext-ciphertext pair (m,c).
We still make use of the randRange() function to generate a random plain letter m and a key pair (k0,k0′). We use this key pair to encrypt m and get c. Now we need to generate 6 random keys ki and another 6 random keys ki′. Use ki to encrypt m we get the set of {ui} and use ki′ to decrypt c we get the set of {vi}. Then if there is a match between any pair of (ui,vi), the counter increases by 1. In each experiment we run 1,000,000 trials and calculates the probability of succeeding in producing a candidate key pair. Then we run the experiments for 100 times and calculate the probability. The result is shown in Figure 3. The average probability is about 75.29%.
(b) To successfully break Double Happy, it means that the candidate key can decrypts all the cipertext
produced from any m  X with the key pair that Alice owns. Due to the special property of Double Happy,
it is suffice to show that if the candidate key pair can decrypts one plaintext-ciphertext pair
(m1,c1)
X with the key pair that Alice owns. Due to the special property of Double Happy,
it is suffice to show that if the candidate key pair can decrypts one plaintext-ciphertext pair
(m1,c1)  X1 and another plaintext-ciphertext pair (m2,c2)
X1 and another plaintext-ciphertext pair (m2,c2)  X2, it can break the entire encryption
system.
X2, it can break the entire encryption
system.
Therefore, we make use of the randRange() function to generate two random plain letter m1  X1 and
m2
X1 and
m2  X2, and a key pair (k0,k0′). We use this key pair to encrypt m1,m2 and get c1,c2. Now we need to
generate 6 random keys ki and another 6 random keys ki′. Use ki to encrypt m we get the set of {ui} and
use ki′ to decrypt c we get the set of {vi}. By finding the match between any pair of (ui,vi),
we find the candidate key pair that can decrypts (m1,c1). If we also succeed in decrypting
(m2,c2) with the same candidate key pair, we have succeeded in producing a candidate key
pair that breaks Double Happy. In each experiment we run 1,000,000 trials and calculates the
probability of succeeding in breaking Double Happy. Then we run the experiments for 100 times and
calculate the probability. The result is shown in Figure 3. The average probability is about
13.53%.
X2, and a key pair (k0,k0′). We use this key pair to encrypt m1,m2 and get c1,c2. Now we need to
generate 6 random keys ki and another 6 random keys ki′. Use ki to encrypt m we get the set of {ui} and
use ki′ to decrypt c we get the set of {vi}. By finding the match between any pair of (ui,vi),
we find the candidate key pair that can decrypts (m1,c1). If we also succeed in decrypting
(m2,c2) with the same candidate key pair, we have succeeded in producing a candidate key
pair that breaks Double Happy. In each experiment we run 1,000,000 trials and calculates the
probability of succeeding in breaking Double Happy. Then we run the experiments for 100 times and
calculate the probability. The result is shown in Figure 3. The average probability is about
13.53%.