In the problems below, “textbook” refers to Douglas R. Stinson, Cryptography: Theory and Practice, Third Edition, Chapman & Hall/CRC, 2006.

Problem 1: Feistel Network

Textbook, problem 3.2.

 
Solution:

In each stage of the Feistel netowrk, it works as follows:

Now we show that the decryption can be done by applying the same encryption algorithm to L_n and R_n, with the reversed key schedule K_n-1,,K₀. Switching the two sides of (1) and applying (⊕f(R_i,K_i)) to both sides of (2), we get

Problem 2: DES Complementation Property

Textbook, problem 3.3.

 
Solution:

y = DES(x,K) and y^′ = DES(c(x),c(K)). The heart of DES is the Feistel network, whose one stage algorithm is described by (1) and (2). For DES(L₀R₀,K), define L₀^′ = c(L₀), R₀^′ = c(R₀) and K_i^′ = c(K_i), which leads to another instance DES(L₀^′R₀^′,K^′). We will show that for any stage of the Feistel network, L_i^′ = c(L_i) and R_i^′ = c(R_i).

• Base: the case when i = 1.

  For instance DES(L₀R₀,K),

  
  For instance DES(L₀^′R₀^′,K^′),
  
  Since f(R_i,K_i) uses the bitwise ⊕ operation to combine input bits of R_i (after expansion) and K_i before the permutation in S-boxes, and ⊕ operation is associative and commutative,

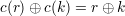  (9)

  Combining (8) and (9) gives

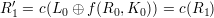  (10)

• Induction: Assume the claim holds for all i < n, consider the case when i = n.

  For instance DES(L₀R₀,K),

  
  For instance DES(L₀^′R₀^′,K^′),
  

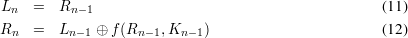
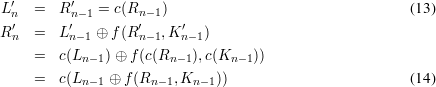
Therefore, after 16 stages of Feistel network, we can get L₁₆^′ = c(L₁₆) and R₁₆^′ = c(R₁₆). Concatenating L₁₆^′ and R₁₆^′, we conclude

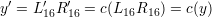(15)

Problem 3: DES S-box S₄

Textbook, problem 3.11(a). [Omit part (b).]

 
Solution:

Each S-box S_i maps an input of six bits to an output of four bits, i.e., S_i : {0,1}⁶ →{0,1}⁴. S_i can be depicted by a 4 × 16 array whose entries are integers in the range [0,15]. Given a six-bit input B = b₀b₁b₂b₃b₄b₅, we compute S_i(B) as follows. The two bits b₀b₅ determine the binary representation of a row r of S_i, where 0 ≤ r ≤ 3, while the four bits b₁b₂b₃b₄ determine the binary representation of a column c of S_i, where 0 ≤ c ≤ 15. Then we find the entry corresponding to row r and column c of the 4 × 16 array, and use it binary representation as the four-bit output.

For the special property of S₄, we need to check the binary representation of each entry one by one. For example, the first entry of the second row is (13)₁₀ = (1101)₂, and the first entry of the first row is (7)₁₀ = (0111)₂. Applying the mapping, we have

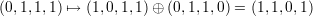(16)

We put the results for all the 16 entries in the table below.

c	first row	mapping	second row
0	(7)10 = (0111)2	(0,1,1,1)(1,0,1,1) ⊕ (0,1,1,0) = (1,1,0,1)	(13)10 = (1101)2
1	(13)10 = (1101)2	(1,1,0,1)(1,1,1,0) ⊕ (0,1,1,0) = (1,0,0,0)	(8)10 = (1000)2
2	(14)10 = (1110)2	(1,1,1,0)(1,1,0,1) ⊕ (0,1,1,0) = (1,0,1,1)	(11)10 = (1011)2
3	(3)10 = (0011)2	(0,0,1,1)(0,0,1,1) ⊕ (0,1,1,0) = (0,1,0,1)	(5)10 = (0101)2
4	(0)10 = (0000)2	(0,0,0,0)(0,0,0,0) ⊕ (0,1,1,0) = (0,1,1,0)	(6)10 = (0110)2
5	(6)10 = (0110)2	(0,1,1,0)(1,0,0,1) ⊕ (0,1,1,0) = (1,1,1,1)	(15)10 = (1111)2
6	(9)10 = (1001)2	(1,0,0,1)(0,1,1,0) ⊕ (0,1,1,0) = (0,0,0,0)	(0)10 = (0000)2
7	(10)10 = (1010)2	(1,0,1,0)(0,1,0,1) ⊕ (0,1,1,0) = (0,0,1,1)	(3)10 = (0011)2
8	(1)10 = (0001)2	(0,0,0,1)(0,0,1,0) ⊕ (0,1,1,0) = (0,1,0,0)	(4)10 = (0100)2
9	(2)10 = (0010)2	(0,0,1,0)(0,0,0,1) ⊕ (0,1,1,0) = (0,1,1,1)	(7)10 = (0111)2
10	(8)10 = (1000)2	(1,0,0,0)(0,1,0,0) ⊕ (0,1,1,0) = (0,0,1,0)	(2)10 = (0010)2
11	(5)10 = (0101)2	(0,1,0,1)(1,0,1,0) ⊕ (0,1,1,0) = (1,1,0,0)	(12)10 = (1100)2
12	(11)10 = (1011)2	(1,0,1,1)(0,1,1,1) ⊕ (0,1,1,0) = (0,0,0,1)	(1)10 = (0001)2
13	(12)10 = (1100)2	(1,1,0,0)(1,1,0,0) ⊕ (0,1,1,0) = (1,0,1,0)	(10)10 = (1010)2
14	(4)10 = (0100)2	(0,1,0,0)(1,0,0,0) ⊕ (0,1,1,0) = (1,1,1,0)	(14)10 = (1110)2
15	(15)10 = (1111)2	(1,1,1,1)(1,1,1,1) ⊕ (0,1,1,0) = (1,0,0,1)	(9)10 = (1001)2

Problem 4: Practice with mod

Read pages 3–4 of textbook and then work the following:

1. Textbook, problem 1.1.
2. Textbook, problem 1.2.
3. Textbook, problem 1.3.
4. Textbook, problem 1.4.

 
Solution:

• Problem 1.1
  1. By the division theorem, 7503 = 92 × 81 + 51, so 7503 mod 81 = 51.
  2. By the division theorem, -7503 = -93 × 81 + 30, so (-7503) mod 81 = 30.
  3. By the division theorem, 81 = 0 × 7503 + 81, so 81 mod 7503 = 81.
  4. By the division theorem, -81 = -1 × 7503 + 7422, so (-81) mod 7503 = 7422
• Problem 1.2

  By the division theorem, a = m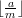 + (a mod m). Therefore, we have

  

  Because a ⁄≡ 0 (mod m), it is easy to see that 0 < a mod m < m, which implies 0 < m - (a mod m) < m. Therefore, we have

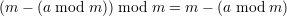  (18)

  Combining (17) and (18), we reach the conclusion that

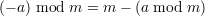  (19)

• Problem 1.3

  By definition, a ≡ b (mod m) ⇔ m∣(a - b). By the division theorem,

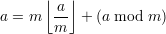  (20)

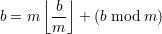  (21)

  . Subtracting (21) from (20) gives

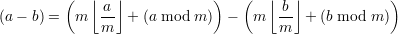  (22)

  Together with the fact that m∣(mu + v) iff m∣v, we have

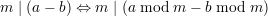  (23)

  Because (i mod m) Z_m, m∣(a mod m-b mod m) iff a mod m = b mod m. In sum, we have shown

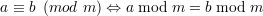  (24)

• Problem 1.4

  By the division theorem, a = km + b, where 0 ≤ b < m. It is obvious b = a mod m. Dividing both sides of the first equation by m, we have 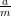= k + 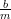. 0 ≤ b < m implies that 0 ≤ 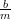< 1, and thus k is the largest integer that is less than or equal to 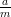, which is precisely the definition of 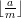. Therefore,

  

Problem 5: Extended Euclidean Algorithm

Textbook, problem 5.3. Show your work.

 
Solution:

a) 17^-1 mod 101 = 6

b) 357^-1 mod 1234 = 1234 - 159 = 1075

c) 3125^-1 mod 9987 = 1844

Problem 6: Linear Diophantine Equations

Textbook, problem 5.4. Show your work.

 
Solution:

gcd(57,93) = 3

s = -13, t = 8

Problem 7: RSA Encryption

[This is problem 6.8.2 from Trapp & Washington, “Introduction to Cryptography with Coding Theory, Second Edition”, Pearson Prentice Hall, 2006.]

Suppose your RSA modulus is n = 55 = 5 × 11 and your encryption exponent is e = 3.

1. Find the decryption modulus d.
2. Assume that gcd(m,55) = 1. Show that if c ≡ m³ (mod 55) is the ciphertext, then the plaintext is m ≡ c^d (mod 55). Do not quote the fact that RSA decryption works. That is what you are showing in this specific case.

 
Solution:

(a) Since n = 55 = 5 × 11, we have ϕ(n) = (5 - 1) × (11 - 1) = 40. Now we apply the Extended Euclidean algorithm to find d given that e = 3.

Therefore, we have d = 40 - 13 = 27.

(b) The question asks us to prove m ≡ c²⁷ (mod 55), given c ≡ m³ (mod 55) and gcd(m,55) = 1. Starting from the first condition, we have

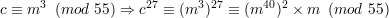(26)

Euler’s theorem says, if gcd(x,n) = 1, then

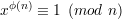(27)

Since ϕ(55) = 40 and gcd(m,55) = 1, combining (26) and (27) gives

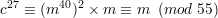(28)

Because congruence is commutative, (28) implies

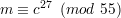(29)