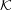 =
= 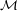 =
= 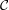 = {0,1,2,3}:
= {0,1,2,3}:
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Handout #13 | |
| Xueyuan Su | November 4, 2008 | |
Solution to Midterm Examination
This is a closed book examination. Answer any 5 of the following 6 questions. Write the numbers of the five questions that you want graded on the cover of your bluebook. All questions count equally. You have 75 minutes. Remember to write your name on your bluebook and to justify your answers. Good Luck!
___________________________________________________________________________________
Problem 1: Symmetric Cryptosystems and Information Security
Consider the encryption function for a symmetric cryptosystem described by the table below, where
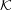 =
= 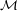 =
= 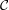 = {0,1,2,3}:
= {0,1,2,3}:
Solution:
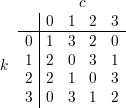
![prob[m = m0 ∧c = c0] = prob[m = m0 ]× prob[c = c0]](ho132x.png) | (1) |
for all m0 
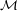 and c0
and c0 
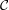 . An equivalent definition in terms of conditional probability
is
. An equivalent definition in terms of conditional probability
is
![prob[m = m | c = c ] = prob[m = m ]
0 0 0](ho133x.png) | (2) |
for all m0 
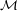 and c0
and c0 
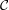 such that prob[c = c0]≠0. Hence, even after Eve receives the ciphertext
c0, her opinion of the likelihood of each message m0 is the same as it was initially, so she has
learned nothing about m0.
such that prob[c = c0]≠0. Hence, even after Eve receives the ciphertext
c0, her opinion of the likelihood of each message m0 is the same as it was initially, so she has
learned nothing about m0.
We have discussed a number of different possible attacks on a cryptosystem by a passive eavesdropper Eve, depending on what information is available to her.
 {0,1}. The encryption function is Ek(m) = c, where c = c1c2…ct and
ci = mi ⊕ b, for i = 1,…,t. Discuss the security of this system under each of the three kinds
of attacks (from part (a) above). Where the system is insecure, describe carefully the sense
in which it insecure. Be sure to say also how the security is affected by the choice of t.
{0,1}. The encryption function is Ek(m) = c, where c = c1c2…ct and
ci = mi ⊕ b, for i = 1,…,t. Discuss the security of this system under each of the three kinds
of attacks (from part (a) above). Where the system is insecure, describe carefully the sense
in which it insecure. Be sure to say also how the security is affected by the choice of t.Solution:
 {c1,…,cr} and wants to recover the
corresponding message m. Eve is able to perform such an attack if the previous
plaintext-ciphertext pairs are revealed by Alice or Bob. Eve might also get information
about the previous plaintext-ciphertext pairs by looking into Alice’s swap files.
{c1,…,cr} and wants to recover the
corresponding message m. Eve is able to perform such an attack if the previous
plaintext-ciphertext pairs are revealed by Alice or Bob. Eve might also get information
about the previous plaintext-ciphertext pairs by looking into Alice’s swap files.
 (the complement of
c).
(the complement of
c).
Recall that the heart of DES is a round of the form:
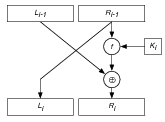
Consider a simplified DES-like cryptosystem consisting of n such rounds, where the function f is defined by fK(X) = K ⊕ X. Here we assume that the key K is 32-bits long and that the same key is used at each round, that is, Ki = K for each round i.
This system is used to encrypt a 64-bit message M as follows: L0 is the leftmost 32-bits of M and R0 is the rightmost 32-bits of M. The ciphertext EK(M) is Ln ⋅ Rn.
Solution:
We remark that, also like DES, the encryption and decryption functions for each round are almost the same. Let EK(Li ⋅ Ri) = Li+1 ⋅ Ri+1 be the encryption function defined by (3). Let DK(Li+1 ⋅Ri+1) = Li ⋅Ri be the corresponding decryption function defined by (4). One can easily verify that
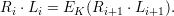 | (5) |
Thus, if S(L⋅R) = R ⋅L is the function that swaps the left and right halves of its 64-bit argument, then it follows from (5) that
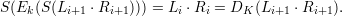 | (6) |
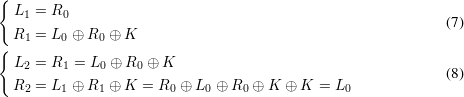
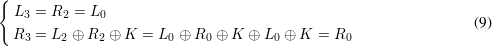
Let (E,D) be a block cipher and let m1,m2,…,mt be a sequence of t plaintext blocks. Happy Hacker was not happy with the chaining modes he learned about in CPSC 467, so he invented his own. He defines a sequence of t + 2 ciphertext blocks c0,c1,c2,…,ct,ct+1 which satisfies the equation
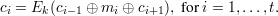
Solution:
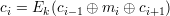 | (10) |
Applying decryption function to both sides of (10) gives
Adding (using ⊕) the expression (⊕ci-1 ⊕ ci+1) to (11) and swapping the two sides gives
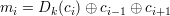 | (12) |
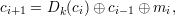 | (13) |
where 1 ≤ i ≤ t. In order to get started, we set c0 and c1 to some fixed initialization vectors.
My toy RSA key is N = 187,e = 107. You observe a ciphertext c = 2. What is the plaintext? (Note: 187 = 11 * 17.)
Solution:
Given N = 187 = 11 × 17, it is easy to compute ϕ(N) = (11 - 1) × (17 - 1) = 160.
Next, given e = 107, which is relative prime to 160, we use extended Euclidean algorithm to compute d such that ed ≡ 1 (mod 107):
| i | ri | ui | vi | qi |
| 1 | 160 | 1 | 0 | |
| 2 | 107 | 0 | 1 | 1 |
| 3 | 53 | 1 | -1 | 2 |
| 4 | 1 | -2 | 3 | |
The result from the table is d = v4 = 3.
Finally we apply the decryption function of RSA to get the plaintext
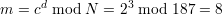 | (14) |
(Hint: This problem is easily solved by hand using Euler’s theorem to reduce the size of the exponents.)
Solution:
 Zn∣gcd(a,n) = 1}, then Euler’s totient function ϕ(n) is the cardinality of Z*n. If
we represent an integer n by its prime factors as follows
Zn∣gcd(a,n) = 1}, then Euler’s totient function ϕ(n) is the cardinality of Z*n. If
we represent an integer n by its prime factors as follows
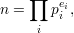 | (15) |
then ϕ(n) can be calculated as
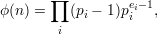 | (16) |
Euler’s theorem says, for every x that is relative prime to n,
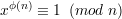 | (17) |
After verifying gcd(5,28) = 1, applying Euler’s theorem gives
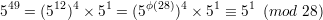 | (18) |
Therefore after verifying gcd(2,29) = 1, we have
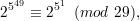 | (19) |
which implies 2549 mod 29 = 251 mod 29 = 3.