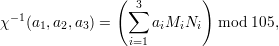
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Handout #15 | |
| Xueyuan Su | November 9, 2008 | |
Solution to Problem Set 4
Due on Monday, November 3, 2008.
In the problems below, “textbook” refers to Douglas R. Stinson, Cryptography: Theory and Practice, Third Edition, Chapman & Hall/CRC, 2006.
Problem 1: Homomorpohic Mapping χ
Textbook, problem 5.5.
Solution:
According to Chinese remainder theorem, define the function χ-1 : Z3 × Z5 × Z7 → Z105 as follows:
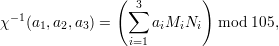 | (1) |
where {ni} = {3,5,7}, Ni = 105∕ni and Mi = Ni-1 mod ni. Therefore, we compute χ-1(a1,a2,a3) as follows:
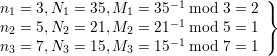
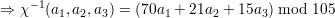 | (2) |
Thus we can compute χ-1(2,2,3) = (70 × 2 + 21 × 2 + 15 × 3) mod 105 = 17.
Problem 2: Chinese Remainder Theorem
Textbook, problem 5.6.
Solution:
According to Chinese remainder theorem, define x as follows:
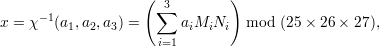 | (3) |
Therefore, we compute χ-1(a1,a2,a3) as follows:
n1 = 25, N1 = 702, M1 = 702-1 mod 25 = (-12) mod 25 = 13.
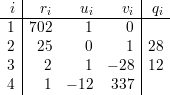
n2 = 26, N2 = 675, M2 = 675-1 mod 26 = (-1) mod 26 = 25.
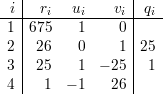
n3 = 27, N3 = 650, M3 = 650-1 mod 27 = (-13) mod 27 = 14.
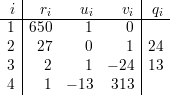
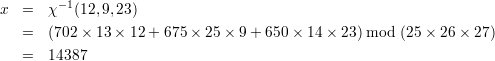
Textbook, problem 5.9.
Solution:
Lucas test says, g is a primitive root of p if and only if g(p-1)∕q ⁄≡ 1 (mod p) for all q > 1 such that q∣(p - 1). Now because p and q are odd primes such that p = 2q + 1, there are only two integers that we need to test with, 2 and q. We know that α ⁄≡±1 (mod p). Then α2 ⁄≡ 1 (mod p) since if it were, α would be a square root of 1 (mod p), and the only square roots of 1 modulo a prime are ±1.
Now let us look at αq. Since p is a prime and α  Z*p, then ϕ(p) = p- 1 = 2q, so by Euler’s theorem,
α2q ≡ 1 (mod p). Then αq is a square root of 1 (mod p), so
Z*p, then ϕ(p) = p- 1 = 2q, so by Euler’s theorem,
α2q ≡ 1 (mod p). Then αq is a square root of 1 (mod p), so
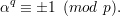 | (4) |
According to Lucas test, α is a primitive root of p if and only if αq ⁄≡ 1 (mod p). Combining this with (4), we conclude that α is a primitive root of p if and only if αq ≡-1 (mod p).
Textbook, problem 5.13.
Solution:
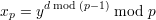 | (10) |
Since p is prime, ϕ(p) = p - 1. According to Euler’s theorem, if gcd(a,p) = 1, then ap-1 ≡ 1 (mod p), which implies
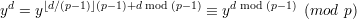 | (11) |
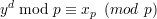 | (12) |
Similarly, from (6) and (8) we can derive
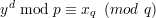 | (13) |
Therefore, according to Chinese reminder theorem, there is a unique solution for yd mod p, which is calculated exactly the same as (9) does. Thus we conclude that the value x returned by this algorithm is in fact yd mod p.
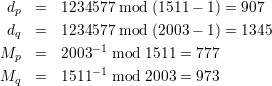
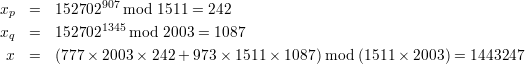
Problem 5: RSA Insecure Against Chosen Ciphertext Attack
Textbook, problem 5.14
Solution:
Let yŷ ≡ 1 (mod n). Then the multiplicative property implies
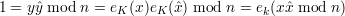 | (14) |
Applying decryption function DK′(⋅) to both sides of (14) and noting DK′(1) = 1, we have
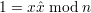 | (15) |
Given 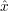 , we can easily compute x using extended Euclidean algorithm.
, we can easily compute x using extended Euclidean algorithm.
Problem 6: RSA Common Modulus Failure
Textbook, problem 5.16.
Solution: