YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE

	CPSC 467a: Cryptography and Computer Security	Handout #20
Xueyuan Su		December 11, 2008

Solution to Problem Set 6

Due before midnight on Wednesday, December 3, 2008.

In the problems below, “textbook” refers to Douglas R. Stinson, Cryptography: Theory and Practice, Third Edition, Chapman & Hall/CRC, 2006.

Problem 1: ElGamal Ciphertext Decryption

Textbook, problem 6.9. An electronic copy of Table 6.3 has been placed on the Zoo in file /c/cs467/assignments/ps6/stinson_table_6.3.txt so that you don’t have to type in all of this input data. Although you will have to implement ElGamal decryption in order to solve this problem, the numbers are all small enough so that you can get by with 32-bit arithmetic rather than using one of the big number packages.

Solution:

Given p = 31847 and a = 7899, using the decryption function on page 235 in the textbook

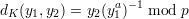d (y ,y ) = y (ya)-1 mod p K 1 2 2 1

(1)

gives the following (formatted) plain text: “She stands up in the garden where she has been working and looks into the distance. She has sensed a change in the weather. There is another gust of wind, a buckle of noise in the air, and the tall cypresses sway. She turns and moves uphill towards the house. Climbing over a low wall, feeling the first drop of rain on her bare arms, she crosses the loggia and quickly enters the house.”

Problem 2: ElGamal Signatures

Textbook, problem 7.3(a).

Solution:

Conforming to the notation we have been used in the class, we have k_i+1 = (k_i + 2) mod ϕ(p) in this problem. According to the signing function, we have

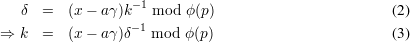
δ = (x - aγ )k- 1 mod ϕ(p) (2) - 1 ⇒ k = (x - aγ )δ mod ϕ(p) (3)

Plugging in the information (x_i,(γ_i,δ_i)) and (x_i+1,(γ_i+1,δ_i+1)) which Bob has observed gives

k = (x - aγ )δ-1mod ϕ(p) (4) i i i i -1 ki+1 = (xi+1 - aγi+1)δi+1 mod ϕ(p) (5)

Subtracting Equation (4) from Equation (5) gives

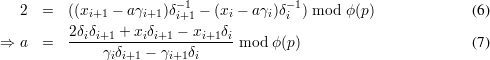
-1 -1 2 = ((xi+1 - aγi+1)δi+1 - (xi - aγi)δi ) mod ϕ(p) (6) 2δiδi+1 + xiδi+1 - xi+1δi ⇒ a = ----γ-δ-----γ---δ------mod ϕ(p) (7) ii+1 i+1 i

Problem 3: Simplified Feige-Fiat Authentication Protocol

Bob is using 20 rounds of the simplified Feige-Fiat authentication protocol presented in section 95 in Lecture Notes 20, thinking that the chance of an impostor successfully impersonating the legitimate Alice is only 2^-20. Unbeknownst to him, there is a bug in the random number generator that he is using to generate b, so prob[b = 1] = 0.9 and prob[b = 0] = 0.1.

What is the probability that an impostor can successfully fool Bob? Argue why your answer is correct.
Describe how the attack works that achieves the probability of part (a) above.

Solution:

Assume the impostor Mallory knows the bug in Bob’s random number generator. Let p be the probability that Mallory guesses 1 and thus 1 - p be the probability of guessing 0. Then the probability that Mallory’s guess is correct in one round is
$Pr{RN G generates 1 ∧M allory guesses 1} +Pr {RN G generates 0 ∧M allory guesses 0} = 0.9p + 0.1(1 - p),$
which is maximized as 0.9 when p = 1. Therefore, if Mallory always guesses 1, he successfully fools Bob after 20 rounds with probability 0.9²⁰ ≈ 0.1216.
As we have shown before, Mallory should always guess 1. Therefore, in each round, Mallory picks an arbitrary y and computes x = y²v mod n. He sends out x in the first step, and he sends the corresponding y in the third step. If the random number generated by Bob is indeed 1, then Mallory successfully fools Bob in this round. By repeating this for 20 rounds, Mallory can reach the success probability 0.9²⁰ ≈ 0.1216.