YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 467a: Cryptography and Computer Security | Notes 1 (rev. 1) |
| Professor M. J. Fischer | | September 3, 2008 |
|
|
|
| |
1 Course Overview
This course is about cryptography and its application to computer and network security. A
better term might be information security, which includes all forms of information protection,
whether the information resides in a computer, on the network, or on a storage device such as a
hard disk, DVD, or even paper. Security is a huge field and includes important non-technical
topics such as incentive, opportunity, deterrence, threat, trust, anonymity, and coercion, all of
which play together into the overall security picture. Our focus is on a particular set of useful
tools—cryptographic primitives—that that can be used to enhance information security. Nevertheless,
we need some awareness of general security issues in order to understand the environment
in which cryptographic tools are used and to motivate the properties that we desire of these
tools.
2 Information Security
The classical information security problem is how to send secret messages over an insecure channel. But
information security is much broader than this. It is also about preventing hackers from breaking into a
computer, preventing denial of service attacks against web servers, preventing unauthorized modification of
databases, preventing illegal copying of data, preventing fraud in e-commerce applications, and so
forth.
Security generally seems to mean preventing bad things from happening. However, it is not always so
easy to decide exactly what are the bad things that one is trying to prevent. Without knowing exactly what
is to be prevented, one can never know how effective a security system is at preventing them. This leads to
the analysis of attack scenarios—the things an adversary might attempt that we’d like to protect against. Of
course, one also wants to allow those activities to proceed normally that are not proscribed by the security
policy.
2.1 A security example from real life
A familiar example of a security problem is that of keeping intruders out of my house.
What do I want to keep out?
Specifying exactly what is to be kept out and what allowed is already not such an easy problem. At first
sight, I might say that I don’t want anybody entering whom I have not specifically authorized. But even this
can be a bit problematical.
- Do I also want to prevent chimpanzees from entering?
- Do I want to prevent mice from entering?
- Do I want to prevent the twin brother of my friend Alex from entering (who looks so much
like Alex that even I can’t always tell them apart)?
While these questions may sound silly, they have serious analogs in information security. To (1), you’d likely
say, “Of course, I don’t want to let chimpanzees in the house either, but I don’t consider them a threat
because there are no chimpanzees in my neighborhood.” Yet the world of information security is
replete with examples of security holes that are of no consequence until someone develops an
exploit, at which time they suddenly become serious problems. To (2), you might say, “No, I
don’t want mice in, either”, but at the same time you’d realize that the means of preventing
mice from entering are quite different from those of protecting against human intruders, and
conflating the two problems will only make finding workable solutions that much harder. To
(3), you’re forced to think about the meaning of identity. What is it about Alex that makes me
want to let him in but not his twin brother? What hope do I have of solving this problem if
I can’t distinguish between the two? In fact, the simple solution of giving Alex a key to the
house works in practice, as long as I know that it is Alex getting the key and not his brother.
Distinguishing among individuals becomes a serious problem on the internet, and schemes
purporting to identify individuals generally identify instead possession of secret information (a
cryptographic key) or a particular object (such as a smart card) instead, with the assumption
that this is sufficient to identify the individual. It isn’t always so in the real world, for secrets
can be stolen and smart cards forged. The rapid growth of identity theft today is evidence of
this fact. (See http://www.ftc.gov/bcp/edu/microsites/idtheft/ for further information on this
topic.)
What are some possible means to keep out intruders, and how effective are they?
We now look at some of the means that might be used to keep intruders out and discuss their
effectiveness.
- Post a ”no trespassing – do not enter” sign.
- Lock the front door.
- Install a burglar alarm.
- Buy a gun.
- Call the police.
- Sue the intruder.
- Conceal the entrance.
Think carefully about each of these means and ask yourself under what conditions it might be effective, and
what else must be in place for it to work. For example, suing the intruder presupposes that
he can be identified, that you have evidence that he entered illegally, and that society has an
effective judicial system. Buying a gun will only deter breakins if it is known that you are likely to
possess a gun. Locking the front door has little effect unless the back door and windows are also
locked.
2.2 Cryptography and security
Cryptography is to information security as locks are to personal security.
- Both are clever mechanisms that can be analyzed in isolation.
- Both can be effective when used in suitable contexts.
- Both comprise only a small part of the security picture.
2.3 Information security in the real world
Here are just some of the many goals of information security.
- Protection against data damage.
- Protection against theft of intellectual property.
- Protection against surveillance.
- Protection against unauthorized actions.
- Protection of constitutional privacy rights.
- Protection of freedom of information.
How is security achieved in the real world?
- Prevention: Physical barriers, locks, encryption, firewalls, etc.
- Detection: Audits, checks and balances.
- Legal means: Laws, sanctions.
- Concealment: Camouflage, steganography.
Absolute security in the real world is infeasible. The goal is risk management. The same is true with
information security. Security mechanisms have a cost. One needs to weight their cost against the
benefits.
3 Organization
The course will be roughly organized around cryptographic primitives, objects having properties
that make them useful in solving certain security problems. For each such primitive, one can
ask:
-
What can be done with it?
- This leads to a study of cryptographic algorithms and
protocols.
-
What are its properties?
- This leads to modeling and analysis, which very quickly
requires complexity theory, probability theory, and statistics.
-
How is it built?
- This requires a fair amount of mathematics, particularly number
theory and algebra. Don’t worry if you haven’t studied these topics before. We
will cover what is need for the methods discussed in this course.
-
How is it implemented?
- Implementing cryptographic primitives requires a lot of
attention to detail, especially to make sure that the programs don’t accidentally
leak secret information. This course will involve some implementation.
4 Computer Science, Mathematics and Cryptography
Cryptography cuts across subareas of both computer science and mathematics. On the computer science
side, cryptographic algorithms and protocols not only carry out sophisticated distributed computations, but
they must be implemented in a way so as to not inadvertantly leak senssitive information. It doesn’t matter
how mathematically strong the mathematical primitive is if a sloppy implementation allows an adversary to
discover the key. There will be some implementation problems to give you a flavor of what it is like to
program cryptographic algorithms.
Mathematics enters the field at several levels. Many cryptographic primitives are based on number
theoretic problems such as factoring and discrete log and on algebraic properties of structures such as
elliptic curves. Understanding and modeling security uses probability theory and coding theory on the one
hand, and complexity theory on the other. We will explore these topics in enough depth to give you some
understanding into how various cryptographic primitives work and why they are believed to be
secure.
5 Example primitive: Symmetric cryptography
A symmetric cryptosystem (sometimes called a private-key or one-key system) is a pair of
efficiently-computable functions E and D such that D(k,E(k,m)) = m for all keys k and
all messages m. Moreover, given c = E(k,m), it is hard to find m without knowing the key
k.
5.1 What can be done with a symmetric cryptosystem?
This is the classical tool for solving the secret message transmission problem:
- Alice wants to send Bob a private message m over the internet.
- Alice and Bob both have a secret key k.
- Alice computes c = E(k,m) and sends c to Bob.
- Bob receives c′, computes m′ = D(k,c′), and assumes m′ to be Alice’s message. [What
happens if c′≠c?]
We assume that the network is insecure and that an eavesdropper, Eve, can listen in and learn c. We desire
nonetheless that m remain private and unknown to Eve.
5.2 What do we require of E, D, and the computing environment in order for this protocol to
accomplish Alice and Bob’s goals?
- Given c, it is hard to find m without also knowing k.
- k is not initially known to Eve.
- Eve can guess k with at most an extremely tiny probability of success. This means k must be
chosen randomly from a large key space.
- Alice and Bob protect k from being released. Their computers have not been compromised.
Eve is not able to obtain k by looking on Alice’s or Bob’s hard disk, swap file, or free memory
pages, even if she is a legitimate user of that computer or the services it provides.
- There are no unanticipated ways by which Eve succeeds in obtaining k, e.g., social
engineering, using binoculars to watch Alice or Bob’s keyboard, etc. etc.
6 Symmetric cryptosystems
A symmetric cryptosystem consists of a set 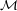 of plaintext messages, a set
of plaintext messages, a set 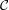 of ciphertexts, a set
of ciphertexts, a set  of keys,
and two functions, an encryption function E :
of keys,
and two functions, an encryption function E :  ×
×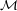 →
→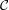 and a decryption function D :
and a decryption function D :  ×
×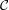 →
→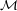 .
We often write Ek(m) = E(k,m) and Dk(c) = D(k,c). One may view a cryptosystem as consisting of a
family of encryption and decryption functions indexed by k, but this should not obscure the fact
that in order to be useful, it must be possible to compute the functions given an arbitrary key
k.
.
We often write Ek(m) = E(k,m) and Dk(c) = D(k,c). One may view a cryptosystem as consisting of a
family of encryption and decryption functions indexed by k, but this should not obscure the fact
that in order to be useful, it must be possible to compute the functions given an arbitrary key
k.
We would like a cryptosystem to have three properties:
-
Decipherability
- ∀m

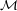 ,∀k
,∀k 
 ,Dk(Ek(m)) = m. In other words, Dk is the left inverse of
Ek.
,Dk(Ek(m)) = m. In other words, Dk is the left inverse of
Ek.
-
Feasibility
- E and D, regarded as functions of two arguments, should be computable using a
feasible amount of time and storage.
-
Security (weak)
- It should be difficult to find m given c = Ek(m) without knowing k.
7 Attack scenarios
While these properties are always required of a cryptosystem, we generally want m to remain secret even
when Eve has access to various kinds of additional information. This leads us to define several attack
scenarios.
-
Ciphertext-only attack
- This is the situation covered by weak security, where Eve knows only c
and tries to recover m.
-
Known plaintext attack
- Here we assume that Eve knows a sequence of plaintext-ciphertext pairs
(m1,c1),…,(mr,cr). Now she obtains a new ciphertext c ⁄
 {c1,…,cr} and wants to recover
the corresponding message m.
{c1,…,cr} and wants to recover
the corresponding message m.
-
Chosen plaintext attack
- This is like a known plaintext attack, except that before getting c, Eve
gets to choose messages m1,…,mr and somehow get Alice (or Bob) to encrypt them for her
and supply her with the corresponding ciphertexts c1,…,cr.
-
Chosen ciphertext attack
- This is like a known plaintext attack, except that before getting c, Eve
gets to choose ciphertexts c1,…,cr and somehow get Alice (or Bob) to decrypt them for her
and supply her with the corresponding plaintext messages m1,…,mr.
Still stronger versions of these attacks are possible. For example, in a chosen plaintext attack, Eve might be
able to choose the messages mi one at a time rather than all at once so that m2 depends on the value of c1,
m3 depends on both c1 and c2, and so forth. Such an attack is called adaptive. Adaptive chosen ciphertext
attacks are of course also possible, where each new ciphertext chosen depends on the plaintexts
corresponding to the previously-chosen ciphertexts. One can have mixed chosen plaintext and
chosen ciphertext attacks where Eve chooses some plaintexts and some ciphertexts and gets the
corresponding decryptions or encryptions of same. Adaptive versions of mixed attacks are also
possible.
One might question whether such attack scenarios are feasible in practice. Why would Alice cooperate
with Eve in this way? It all depends on the situation in which the cryptosystem is used. “Alice” might be an
Internet server, not a person, who encrypts/decrypts certain messages received in the course of carrying out
a more complicated cryptographic protocol. We will see such protocols later in the course. One could
also imagine that an attacker gets hold of Alice’s encryption device and is able to play with
it for awhile even though she can’t extract the secret key that is stored inside. For example,
Eve might sit down at Alice’s computer when Alice is out to lunch, or she might slip Alice’s
cryptographic smart card out of her purse when Alice isn’t looking. Of course, if Alice discovers the
intrusion or learns that her card is missing, she’ll change her key and Eve’s efforts would be for
naught, but if Eve puts everything back in order before Alice returns, Alice might be none the
wiser.
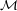 of plaintext messages, a set
of plaintext messages, a set 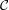 of ciphertexts, a set
of ciphertexts, a set  of keys,
and two functions, an encryption function E :
of keys,
and two functions, an encryption function E :  ×
×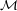 →
→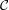 and a decryption function D :
and a decryption function D :  ×
×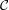 →
→ .
We often write Ek(m) = E(k,m) and Dk(c) = D(k,c). One may view a cryptosystem as consisting of a
family of encryption and decryption functions indexed by k, but this should not obscure the fact
that in order to be useful, it must be possible to compute the functions given an arbitrary key
k.
.
We often write Ek(m) = E(k,m) and Dk(c) = D(k,c). One may view a cryptosystem as consisting of a
family of encryption and decryption functions indexed by k, but this should not obscure the fact
that in order to be useful, it must be possible to compute the functions given an arbitrary key
k.
