37 Asymmetric Cryptosystems

A major advance in cryptography is the modern development of asymmetric (also called 2-key or public key) cryptosystems. The idea is simple. Instead of having a single key k that is used by both Alice and Bob, an asymmetric cryptosystem has a pair of related keys, an encryption key e and a decryption key d. Alice encrypts a message m by computing c = E_e(m). Bob decrypts by computing m = D_d(c).¹ As always, the decryption function inverts the encryption function, so the following is always satisfied:

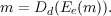
What makes asymmetric systems useful is the additional requirement that it be difficult to find d from e, and more generally, that it be difficult to find m given both e and c = E_e(m). Thus, the system remains secure even if the encryption key e is made public!

There are several reasons to make e public. One is that it is then possible for anybody to send a private message to Bob. Sandra need only obtain Bob’s public key e and send Bob E_e(m). Bob recovers m by applying D_d to the received ciphertext. This greatly simplifies the key management problem, for there is no longer the need for a secure channel between Alice and Bob for the initial key distribution (which I have carefully avoided talking about so far).

Of course, an active adversary Mallory can still do some nasty things. For example, he could send his own encryption key to Sandra when she attempts to obtain Bob’s key. Not knowing she has been duped, Sandra would then encrypt her private data in a way that Bob could not read but Mallory could! If Mallory wanted to carry out this charade for a longer time without being discovered, he could intercept each message from Sandra to Bob, decrypt the message using his own decryption key, then re-encrypt it using Bob’s public encryption key and send it on its way. Bob, receiving a validly encrypted message, will be none the wiser to Mallory’s shenanigans. This is another example of a man-in-the-middle attack.

The security requirements for an asymmetric cryptosystem are more stringent than for a symmetric cryptosystem. For example, the system must be secure against large-scale chosen plaintext attacks, for Eve can generate as many plaintext-ciphertext pairs as she wishes using the public encryption function E_e().

The public encryption function also gives Eve a way to check the validity of a potential decryption. Namely, if Eve guesses that D_d(c) = m₀ for some candidate message m₀, she can check her guess by testing if c = E_e(m₀). Thus, whether or not there is redundancy in the set of meaningful messages is of no consequence to her since she now has an independent way of determining a successful decryption.

Designing a good asymmetric cryptosystem is much harder than designing a good symmetric cryptosystem. All of the known asymmetric systems are orders of magnitude slower than corresponding symmetric systems. Therefore, they are often used in conjunction with a symmetric cipher to form a hybrid system. Here’s how this works. Suppose (E²,D²) is a 2-key cryptosystem and (E¹,D¹) is a 1-key cryptosystem. To send a secret message m to Bob, Alice first generates a random session key k for use with the 1-key system. which she then uses to encrypt m. She then encrypts the session key using Bob’s public key for the 2-key system and sends Bob both ciphertexts. In formulas, she sends Bob c₁ = E_k¹(m) and c₂ = E_e²(k). Bob decrypts c₂ using D_d²() to obtain k and then decrypts c₁ using D_k¹() to obtain m. This is much more efficient than simply sending D_e²(m) in the common case that m is much longer than k.

38 RSA

Probably the most commonly used asymmetric cryptosystem today is RSA, named from the initials of its three inventors, Rivest, Shamir, and Adelman. Unlike the symmetric systems we have been talking about so far, RSA is based not on substitution and transposition but on arithmetic involving very large integers, numbers that are hundreds or even thousands of bits long. To understand how RSA works requires knowing a bit of number theory, which we will be presenting in the next few lectures. However, the basic ideas can be presented quite simply, which I will do now.

RSA assumes the message space, ciphertext space, and key space are the set of integers between 0 and n- 1 for some large n. For now, think of n as a number so large that its binary representation is 1024 bits long. To use RSA in the usual case where we are interested in sending bit strings, Alice must first convert her message to an integer, and Bob must convert the integer he gets from decryption back to a bit string. Many such encodings are possible, but perhaps the simplest is to prepend a “1” to the bit string x and regard the result as a binary integer m. To decode m to a bit string, write out m in binary and then delete the initial “1” bit. To ensure that m < n as required, we will limit the length of our binary messages to 1022 bits.

Here’s how RSA works. Alice chooses two sufficiently large prime numbers p and q and computes n = pq. For security, p and q should be about the same length (when written in binary). She then computes two numbers e and d with a certain number-theoretic relationship. The public key is the pair (e,n) The private key is the pair (d,n). The primes p and q are no longer needed and should be discarded.

To encrypt, Alice computes c = m^e mod n. ² To decrypt, Bob computes m = c^d (mod n). Here, a mod n denotes the remainder when a is divided by n. That’s all there is to it, once the keys have been found. It turns out that most of the complexity in implementing RSA has to do with key generation, which fortunately is done only infrequently.

You should already be asking yourself the following questions:

• What are the desired properties that make RSA work? A priori, it seems pretty unlikely that D_d(E_e(m)) = (m^e mod n)^d mod n = m.
• How does one find p, q, e, d with the desired properties?
• Why is RSA believed to be secure?
• How can one implement RSA on a computer when most computers only support arithmetic on 32-bit or 64-bit integers, and how long does it take?
• How can one possibly compute m^e mod n for 1024 bit numbers. m^e, before taking the remainder, has size roughly

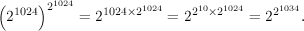
  This is a number that is roughly 2¹⁰³⁴ bits long! No computer has enough memory to store that number, and no computer is fast enough to compute it.

To answer these questions will require the study of clever algorithms for primality testing, fast exponentiation, and modular inverse computation. It will also require some theory of Z_n, the integers modulo n, and some properties of numbers n that are the product of two primes. In particular, the security of RSA is based on the premise that the factoring problem on large integers is infeasible, that is, given n that is known to be the the product of two primes p and q, to find p and q.

39 Computation with Big Integers

The security of RSA depends on n,p,q being sufficiently large. What is sufficiently large? That’s hard to say, but n is typically chosen to be at leasat 1024 bits long, or for better security, 2048 bits long. The primes p and q whose product is n are generally chosen be almost equally long, which means they will each be about half as long as n. Such big numbers present a major computational problem since the arithmetic built into typical computers can handle only 32-bit or 64-bit integers. This means that all arithmetic on large integers must be performed by software routines.

The straightforward algorithms for addition and multiplication that you learned in grade school have time complexities O(N) and O(N²), respectively, where N is the length (in bits) of the integers involved. Asymptotically faster multiplication algorithms are known, but they involve large constant factor overheads, so it’s not clear whether they are practical for numbers of the size we are talking about. What is clear is that a lot of cleverness is possible in the careful implementation of even the O(N²) multiplication algorithms, and a good implementation can be many times faster in practice than a poor one. They are also not particularly easy to get right since there are many special cases that must be handled correctly.

Most people choose to use big number libraries written by others rather than write their own code. Two such libraries that you can use in this course are gmp (Gnu Multiprecision Package), and the big number routines in the openssl crypto library. Gmp provides a large number of highly-optimized function calls for use with C and C++. It is preinstalled on all of the Zoo nodes and supported by the open source community. Type info gmp at a shell for documentation. Openssl is an open source implementation of the Secure Socket Layer protocol and is widely used. The protocol uses cryptography, and openssl uses its own big number routines which are contained in its crypo library. Type man crypto for general information about the library, and man bn for the specifics of the big number routines.

40 Exponentiation: Controlling Growth of Intermediate Results

We now turn to the basic operation of RSA, modular exponentiation of big numbers. This is the problem of computing m^e mod n for big numbers m, e, and n.

The obvious way to compute this would be to compute t = m^e and then compute t mod n. The first problem with this approach is that m^e is too big! m and e are both numbers about 1024 bits long, so their values are each about 2¹⁰²⁴. The value of t is then (2¹⁰²⁴)²¹⁰²⁴ . This number, when written in binary, is about 1024 * 2¹⁰²⁴ bits long, a number far larger than the number of atoms in the universe (which is estimated to be only around 10⁸⁰ ≈ 2²⁶⁶). The trick to get around this problem is to do all arithmetic modulo n, that is, reduce the result modulo n after each arithmetic operation. The product of two length ℓ numbers is only length 2ℓ before reduction mod n, so in this way, one never has to deal with numbers longer than about 2048 bits.