41 Exponentiation: Speeding up the Computation

In section 40 (lecture notes 8), we described how to control the growth in the lengths of numbers when computing m^e mod n, for numbers m, e, and n which are 1024 bits long. Nevertheless, there is still a problem with the naive exponentiation algorithm that simply multiplies m by itself a total of e - 1 times. Since the value of e is roughly 2¹⁰²⁴, that many iterations of the main loop would be required, and the computation would run longer than the current age of the universe (which is estimated to be 15 billion years). Assuming one loop iteration could be done in one microsecond (very optimistic seeing as each iteration requires computing a product and remainder of big numbers), only about 30 × 10¹² iterations could be performed per year, and only about 450 × 10²¹ iterations in the lifetime of the universe. But 450 × 10²¹ ≈ 2⁷⁹, far less than e - 1.

The trick here is to use a more efficient exponentiation algorithm based on repeated squaring. To compute m^e mod n where e = 2^k is a power of two requires only k squarings, i.e., one computes

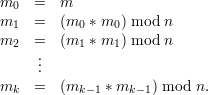
Clearly, each m_i = m²ⁱ mod n. m^e for values of e that are not powers of 2 can be obtained as the product modulo n of certain m_i’s. In particular, express e in binary as e = (b_sb_s-1…b₂b₁b₀)₂. Then m_i is included in the final product if and only if b_i = 1.

It is not necessary to perform this computation in two phases as described above. Rather, the two phases can be combined together, resulting in a slicker and simpler algorithm that does not require the explicit storage of the m_i’s. I will give two versions of the resulting algorithm, a recursive version and an iterative version. I’ll write both in C notation, but it should be understood that the C programs only work for numbers smaller than 2¹⁶. To handle larger numbers requires the use of big number functions.

This same idea can be expressed iteratively to achieve even greater efficiency.

The loop invariant is e > 0 ∧ (m₀^e₀ mod n = rm^e mod n), where m₀ and e₀ are the initial values of m and e, respectively. It is easily checked that this holds at the start of each iteration. If the loop exits, then e = 0, so r is the desired result. Termination is ensured since e gets reduced during each iteration.

Note that the last iteration of the loop computes a new value of m that is never used. A slight efficiency improvement results from restructuring the code to eliminate this unnecessary computation. Following is one way of doing so.

42 Modular Arithmetic

In this and following sections, we review some number theory that is needed for understanding RSA. These lecture notes only provide a high-level overview. Further details are contained in course handouts 5–7 and in Chapter 5 of the textbook (Stinson).

42.1 Division theorem: quotient and remainder

Let a,b be integers and assume b > 0. The division theorem asserts that there are unique integers q (the quotient) and r (the remainder) such that a = bq + r and 0 ≤ r < b. We denote the quotient by a÷b and the remainder by a mod b. It follows that

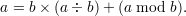
or equivalently,

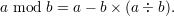
The latter actually defines mod in terms of ‘÷’. The ‘÷’ operator in turn can be defined as a÷b = ⌊a∕b⌋, where ‘∕’ is ordinary real division and ⌊x⌋, the floor of x, is the greatest integer less than or equal to x.

When either a or b is negative, there is no consensus on the definition of mod. According to our definition, a mod b is always in the range [0…b - 1], even when a is negative. For example,

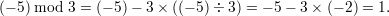
In the C programming language, the mod operator % is defined differently, so (a%b)≠(a mod b) when a is negative and b positive.¹

42.2 Divides

We say that b divides a (exactly) and write b∣a in case a mod b = 0. Fact If d∣(a + b), then either d divides both a and b, or d divides neither of them.

To see this, suppose d∣(a + b) and d∣a. Then by the division theorem, a + b = dq₁ and a = dq₂ for some integers q₁ and q₂. Substituting for a and solving for b, we get

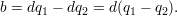
But this implies d∣b, again by the division theorem.

42.3 Modular Arithmetic

We just saw that mod is a binary operation on integers. Mod is also used to denote a relationship on integers:

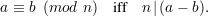
That is, a and b have the same remainder when divided by n. An immediate consequence of this definition is that

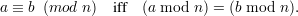
Thus, the two notions of mod aren’t so different after all!

For fixed n, the resulting two-place relationship ≡ is an equivalence relation. Its equivalence classes are called residue classes modulo n and are denoted using the square-bracket notation [b] = {a∣a ≡ b (mod n)}. For example, for n = 7, we have [10] = {… - 11,-4,3,10,17,…}. Clearly, [a] = [b] iff a ≡ b (mod n). Thus, [-11], [-4], [3], [10], [17] are all names for the same equivalence class. We choose the unique integer in the class that is in the range [0…(n - 1)] to be the canonical or preferred name for the class. Thus, the canonical name for the class containing 10 is [10 mod 7] = [3].

The relation ≡ (mod n) is a congruence relation with respect to addition, subtraction, and multiplication of integers. This means that for each of these arithmetic operations ⊙, if a ≡ a′ (mod n) and b ≡ b′ (mod n), then a ⊙ b ≡ a′⊙ b′ (mod n). This implies that the class containing the result of a + b, a - b, or a × b depends only on the classes to which a and b belong and not the particular representatives chosen. Hence, we can perform arithmetic on equivalence classes by operating on their names. The result class will not depend on the particular representatives chosen.

Let Z denote the set of all integers, positive and negative. Let Z_n ⊆ Z contain the non-negative integers less than n, that is,

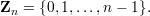
We now define addition, subtraction, and multiplication operations directly on Z_n:

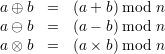(1)

We will sometimes write +,-,× in place of ⊕,⊖,⊗, respectively, when it is clear from context that they are to be regarded as operations over Z_n rather than over Z.

42.4 Greatest common divisor

The greatest common divisor of two integers a and b, written gcd(a,b), is the largest integer d such that d∣a and d∣b. The gcd is always defined since 1 is a divisor of every integer, and the divisor of a number cannot be larger (in absolute value) than the number itself.

The gcd of a and b is easily found if a and b are already given in factored form. Namely, let p_i be the i^th prime and write a = ∏ p_i^e_i and b = ∏p_i^f_i. Then gcd(a,b) = ∏p_i^min(e_i,f_i). However, factoring is believed to be a hard problem, and no polynomial-time factorization algorithm is currently known. Indeed, if it were, then Eve could use it to break RSA, and RSA would be of no interest as a cryptosystem. Fortunately, gcd(a,b) can be computed efficiently without the need to factor a and b using the famous Euclidean algorithm.

42.5 Euclidean algorithm

Euclid’s algorithm is remarkable, not only because it was discovered a very long time ago, but also because it works without knowing the factorization of a and b. It relies on several identities satisfied by the gcd function. In the following, assume a > 0 and a ≥ b ≥ 0:

These identities allow the problem of computing gcd(a,b) to be reduced to the problem of computing gcd(a - b,b), which is “smaller” problem as long as b > 0. Here we measure the size of the problem gcd(a,b) by the sum a + b of the two arguments. This leads to an easy recursive algorithm shown in Figure 42.1. Nevertheless, this algorithm is not very efficient, as you will quickly discover if you attempt to use it, say, to compute gcd(1000000,2).

Repeatedly applying (4) to the pair (a,b) until it can’t be applied any more produces the sequence of pairs (a,b),(a-b,b),(a- 2b,b),…,(a-qb,b). The sequence stops when a-qb < b. But the number of times you can subtract b from a while remaining non-negative is just the quotient ⌊a∕b⌋, and the amount a-qb that is left is just the remainder a mod b. Hence, one can go directly from the pair (a,b) to the pair (a mod b,b), giving the identity

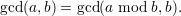(5)

Replacing a-b with a%b in line 5 of Algorithm 42.1 (using C notation) yields an exponentially faster algorithm, one that can be shown to require at most in O(n) stages, where n is the sum of the lengths of a and b when written in binary notation, and each stage involves at most one remainder computation. In addition, line 3 of Algorithm 42.1 can be eliminated if the arguments to the recursive call in line 5 are reversed. In this way, we have a ≥ b for all but the top-level call on gcd(a,b), eliminating the roughly half of the recursive calls whose only effect is to swap the order of arguments.

The full Euclidean algorithm is shown in Figure 42.2.