YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE

CPSC 467a: Cryptography and Computer Security Notes 10 (rev. 1)
Professor M. J. Fischer October 8, 2008

Lecture Notes 10

43 Modular Multiplication

Two integers a and b are relatively prime if they have no common prime factors, or equivalently, if gcd(a,b) = 1. Let Z* n ⊆ Zn contain those integers that are relatively prime to n, so

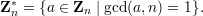
* Z n = {a ∈ Zn | gcd (a,n ) = 1}.

Define Euler’s totient function to be the cardinality of Z*n:

ϕ (n) = |Z*|. n

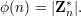
Properties of ϕ(n):

  1. If p is prime, then ϕ(p) = p - 1.
  2. More generally, if p is prime and k ≥ 1, then ϕ(pk) = pk - pk-1 = (p - 1)pk-1.
  3. If gcd(m,n) = 1, then ϕ(mn) = ϕ(m)ϕ(n).

These properties enable one to compute ϕ(n) for all n ≥ 1 provided one knows the factorization of n. For example,

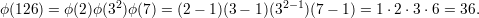
ϕ (126) = ϕ(2)ϕ(32)ϕ(7) = (2 - 1)(3- 1)(32-1)(7 - 1) = 1⋅2 ⋅3⋅6 = 36.

The 36 elements of Z*126 are: 1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41, 43, 47, 53, 55, 59, 61, 65, 67, 71, 73, 79, 83, 85, 89, 95, 97, 101, 103, 107, 109, 113, 115, 121, 125.

44 Modular Exponentiation and Euler’s Theorem

Recall the RSA encryption and decryption functions

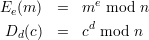
e Ee(m ) = m mod n Dd(c) = cd mod n
where n = pq is the product of two distinct large primes p and q. We see that both are based on modular exponentiation of large integers, an operation that we now explore in some depth.

In section 42.3, we defined the operation ⊗ on all of Zn. An important fact is that Z*n is closed under ⊗, that is, if a and b are both in Z*n, then a ⊗ b is also in Z*n. This follows from the observation that if neither a nor b share a prime factor with n, then neither does their product ab. It can be shown that Z*n is an Abelian group under the operation of ⊗. This means that it satisfies the following properties:

Associativity
⊗ is an associative binary operation on Z*n. In particular, Z*n is closed under ⊗.
Identity
1 is an identity element for ⊗ in Z*n, that is 1 ⋅ x = x ⋅ 1 = x for all x ∈ Z*n.
Inverses
For all x ∈ Z*n, there exists another element x-1 ∈ Z*n such that x⋅x-1 = x-1 ⋅x = 1.
Commutativity
⊗ is commutative. (This is only true for Abelian groups.)

Example: Let n = 26 = 2 ⋅ 13. Then

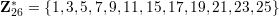
Z *26 = {1,3,5,7,9,11,15,17,19,21,23,25}

and

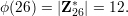
ϕ (26) = |Z* | = 12. 26

The inverses of the elements in Z*26 are given in Table 1.

Table 1: Table of inverses in Z*26.
| x |1 3 5 7 9 11 15 17 19 21 23 25 -----|------------------------------------------------- x-1 |1 9 21 15 3 19 7 23 11 5 17 25 = |1 9 - 5 - 11 3 - 7 7 - 3 11 5 - 9 - 1

The bottom row of the table gives equivalent integers in the range [-12,…,13]. This makes it apparent that (26 -x)-1 = -x-1. In other words, the last row reads back to front the same as it does from front to back except that all of the signs flip from + to - or - to +, so once the inverses for the first six numbers are known, the rest of the table is easily filled in.

It is not obvious from what I have said so far that inverses always exist for members of Z*n. The fact that they do will become apparent later when we show how to compute inverses.

Recall Euler’s ϕ function which was defined in section 43 to be |Z*n|, the cardinality of Z*n. From the properties given there, one can derive an explicit formula for ϕ(n).

Theorem 1 Write n in factored form, so n = p1e1⋅⋅⋅pkek. where p1,…,pk are distinct primes and e1,…,ek are positive integers.1 Then

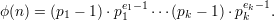
e- 1 e-1 ϕ(n ) = (p1 - 1 )⋅p11 ⋅⋅⋅(pk - 1)⋅p kk .

When p is prime, we have simply ϕ(p) = (p - 1), and for the product of two distinct primes, ϕ(pq) = (p - 1)(q - 1). Thus, ϕ(26) = (13 - 1)(2 - 1) = 12, as we have seen.

A general property of finite groups is that if any element x is repeatedly multiplied by itself, the result is eventually 1. That is, 1 appears in the sequence x,(x ⊗ x),(x ⊗ x ⊗ x),…, after which the sequence repeats. For example, for x = 5 in Z*26, we get the sequence 5,25,21,1,5,25,21,1,…. The result of multiplying x by itself k times can be written xk. The smallest integer k for which xk = 1 is called the order of x, sometimes written ord(x). It follows from general properties of groups that the order of any element of a group divides the order of the group. For Z*n, we therefore have ord(x)∣ϕ(n). From this fact, we immediately get

Theorem 2 (Euler’s theorem) xϕ(n) ≡ 1 (mod n) for all x ∈ Z*n.

As a special case, we have

Theorem 3 (Fermat’s theorem) x(p-1) ≡ 1 (mod p) for all x, 1 ≤ x ≤ p-1, where p is prime.

Corollary 4 Let r ≡ s (mod ϕ(n)). Then ar ≡ as (mod n) for all a ∈ Z*n.

Proof: If r ≡ s (mod ϕ(n)), then r = s + uϕ(n) for some integer u. Then using Euler’s theorem, we have
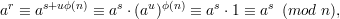
r s+u ϕ(n) s u ϕ(n) s s a ≡ a ≡ a ⋅(a ) ≡ a ⋅1 ≡ a (mod n),

as desired. __

The importance of this corollary to RSA is that it gives us a condition on e and d that ensures the resulting cryptosystem works. That is, if we require that

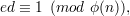ed ≡ 1 (mod ϕ (n )),
(1)

then it follows from Corollary 4 that Dd(Ee(m)) = med ≡ m (mod n) for all messages m ∈ Z*n, so Dd() really does decrypt messages in Z*n that are encrypted by Ee().

What about the case of messages m ∈ Zn - Z*n? There are several answers to this question.

  1. For such m, either p∣m or q∣m (but not both because m < pq). If Alice ever sends such a message and Eve is astute enough to compute gcd(m,n) (which she can easily do), then Eve will succeed in breaking the cryptosystem. So Alice doesn’t really want to send such messages if she can avoid it.
  2. If Alice sends random messages, her probability of choosing a message not in Z*n is only about 2∕√-- n. This is because the number of “bad” messages is only n - ϕ(n) = pq - (p - 1)(q - 1) = p + q - 1 out of a total of n = pq messages altogether. If p and q are both 512 bits long, then the probability of choosing a bad message is only about 2 ⋅ 2512∕21024 = 1∕2511. Such a small probability event will likely never occur during the lifetime of the universe.
  3. For the purists out there, RSA does in fact work for all m ∈ Zn, even though Euler’s theorem fails for m ⁄∈ Z*n. For example, if m = 0, it is clear that (0e)d ≡ 0 (mod n), yet Euler’s theorem fails since 0ϕ(n) ⁄≡ 1 (mod n). We omit the proof of this curiosity.