 Z*
n if e and d are chosen
so that
Z*
n if e and d are chosen
so that
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Notes 11 (rev. 1) | |
| Professor M. J. Fischer | October 13, 2008 | |
Lecture Notes 11
We showed in section 44 (lecture notes 10) that RSA decryption works for m  Z*
n if e and d are chosen
so that
Z*
n if e and d are chosen
so that
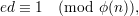 | (1) |
that is, d is e-1 (the inverse of e) in Z*ϕ(n).
We now turn to the question of how Alice chooses e and d to satisfy (1). One way she can do this is to
choose a random integer e  Z*ϕ(n) and then solve (1) for d. We will show how to solve for d in
Sections 46 and 47 below.
Z*ϕ(n) and then solve (1) for d. We will show how to solve for d in
Sections 46 and 47 below.
However, there is another issue, namely, how does Alice find random e  Z*ϕ(n)?
If Z*ϕ(n) is large enough, then she can just choose random elements from Zϕ(n) until
she encounters one that also lies in Z*ϕ(n). A candidate element e lies in Z*ϕ(n) if
gcd(e,ϕ(n)) = 1, which can be computed efficiently using Algorithm 42.2 (Euclidean
algorithm).1
Z*ϕ(n)?
If Z*ϕ(n) is large enough, then she can just choose random elements from Zϕ(n) until
she encounters one that also lies in Z*ϕ(n). A candidate element e lies in Z*ϕ(n) if
gcd(e,ϕ(n)) = 1, which can be computed efficiently using Algorithm 42.2 (Euclidean
algorithm).1
But how large is large enough? If ϕ(ϕ(n)) (the size of Z*ϕ(n)) is much smaller than ϕ(n) (the size of Zϕ(n)), Alice might have to search for a long time before finding a suitable candidate for e.
In general, Z*m can be considerably smaller than m. For example, if m = |Zm| = 210, then |Z*m| = 48. In this case, the probability that a randomly-chosen element of Zm falls in Z*m is only 48∕210 = 8∕35 = 0.228… .
The following theorem provides a crude lower bound on how small Z*m can be relative to the size of Zm that is nevertheless sufficient for our purposes.
Proof: Write m in factored form as m = ∏ i=1tpiei, where pi is the ith prime that divides m and ei ≥ 1. Then ϕ(m) = ∏ i=1t(pi - 1)piei-1, so
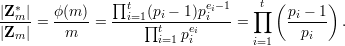 | (2) |
To estimate the size of ∏ i=1t(pi - 1)∕pi, note that (pi - 1)∕pi ≥ i∕(i + 1). This follows since (x- 1)∕x is monotonic increasing in x, and pi ≥ i + 1. Then
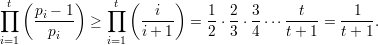 | (3) |
Clearly t ≤⌊log 2m⌋ since 2t ≤∏ i=1tpi ≤ m and t is an integer. Combining this fact with equations (2) and (3) gives the desired result. __
For n a 1024-bit integer, ϕ(n) < n < 21024. Hence, log 2(ϕ(n)) < 1024, so ⌊log 2(ϕ(n))⌋≤ 1023. By Theorem 1, the fraction of elements in Zϕ(n) that also lie in Z*ϕ(n) is at least 1/1024. Therefore, the expected number of random trials before Alice finds a number in Z*ϕ(n) is provably at most 1024 and is most likely much smaller.
Now that Alice knows how to choose e  Z*ϕ(n), how does she find d? That is, how does she solve (1)?
Note that d, if it exists, is a multiplicative inverse of e (mod n), that is, a number that, when multiplied by
e, gives 1 (mod n).
Z*ϕ(n), how does she find d? That is, how does she solve (1)?
Note that d, if it exists, is a multiplicative inverse of e (mod n), that is, a number that, when multiplied by
e, gives 1 (mod n).
Equation (1) is an instance of the general Diophantine equation
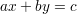 | (4) |
Here, a,b,c are given integers. A solution consists of integer values for the unknowns x and y. To put (1) into this form, we note that ed ≡ 1 (mod ϕ(n)) iff ed + uϕ(n) = 1 for some integer u. This is seen to be an equation in the form of (4) where the unknowns x and y are d and u, respectively, and the coefficients a,b,c are e,ϕ(n),1, respectively.
It turns out that (4) is closely related to the greatest common divisor, for it has a solution iff gcd(a,b)∣c. It can be solved by a process akin to the Euclidean algorithm, which we call the Extended Euclidean algorithm. Here’s how it works.
The algorithm generates a sequence of triples of numbers Ti = (ri,ui,vi), each satisfying the invariant
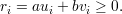 | (5) |
The first triple T1 is (a,1,0) if a ≥ 0 and (-a,-1,0) if a < 0. The second trip T2 is (b,0,1) if b ≥ 0 and (-b,0,-1) if b < 0.
The algorithm generates Ti+2 from Ti and Ti+1 much the same as the Euclidean algorithm generates (a mod b) from a and b. More precisely, let qi+1 = ⌊ri∕ri+1⌋. Then Ti+2 = Ti - qi+1Ti+1, that is,
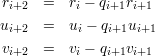
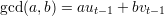 | (6) |
Returning to equation (4), if c = gcd(a,b), then x = ut-1 and y = vt-1 is a solution. If c is a multiple of gcd(a,b), then c = k gcd(a,b) for some k and x = kut-1 and y = kvt-1 is a solution. Otherwise, gcd(a,b) does not divide c, and one can show that (4) has no solution. See Handout 6 for further details, as well as for a discussion of how many solutions (4) has and how to find all solutions.
Here’s an example. Suppose one wants to solve the equation
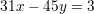 | (7) |
In this example, a = 31 and b = -45. We begin with the triples
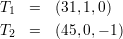
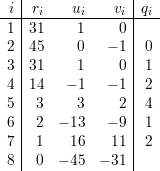
From T7 = (1,16,11) and (5), we obtain
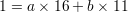
Plugging in values a = 31 and b = -45, we compute
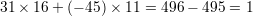
as desired. The solution to (7) is then x = 3 × 16 = 48 and y = 3 × 11 = 33.