YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Notes 12 (rev. 1) | |
| Professor M. J. Fischer | October 15, 2008 | |
Lecture Notes 12
We finally turn to the question of generating the RSA modulus, n = pq. Recall that the numbers p and q should be random distinct primes of about the same length. The method for finding p and q is similar to the “guess-and-check” method used in Section 45 to find random numbers in Z* n. Namely, keep generating random numbers p of the right length until a prime is found. Then keep generating random numbers q of the right length until one is found that is prime and different from p.
To generate a random prime of a given length, say k bits long, generate k - 1 random bits, put a “1” at the front, regard the result as binary number, and test if it is prime. We defer the question of how to test if the number is prime and look now at the expected number of trials before this procedure will terminate.
The above procedure samples uniformly from the set Bk = Z2k - Z2k-1 of binary numbers of length exactly k. Let pk be the fraction of elements in Bk that are prime. Then the expected number of trials to find a prime will be 1∕pk. While pk is difficult to determine exactly, the celebrated Prime Number Theorem allows us to get a good estimate on that number.
Let π(n) be the number of numbers ≤ n that are prime. For example, π(10) = 4 since there are four primes ≤ 10, namely, 2, 3, 5, 7. The prime number theorem asserts that π(n) is “approximately”1 n∕(lnn), where lnn is the natural logarithm log en.2 The chance that a randomly picked number in Zn is prime is then π(n-1)∕n ≈ ((n-1)∕ln(n-1))∕n ≈ 1∕(lnn).
Since Bk = Z2k - Z2k-1, we have
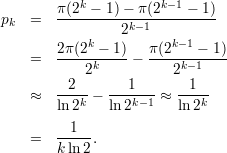
The remaining problem for generating an RSA key is how to test if a large number is prime. Until very recently, no deterministic polynomial time algorithm was known for testing primality, and even now it is not known whether any deterministic algorithm is feasible in practice. However, there do exist fast probabilistic algorithms for testing primality, which we now discuss.
A deterministic test for primality is a procedure that, given as input an integer n ≥ 2, correctly returns the answer ‘composite’ or ‘prime’. To arrive at a probabilistic algorithm, we extend the notion of a deterministic primality test in two ways: We give it an extra “helper” string a, and we allow it to answer ‘?’, meaning “I don’t know”. Given input n and helper string a, such an algorithm may correctly answer either ‘composite’ or ‘?’ when n is composite, and it may correctly answer either ‘prime’ or ‘?’ when n is prime. If the algorithm gives a non-”?” answer, we say that the helper string a is a witness to that answer.
We can use an extended primality test T(n,a) to build a strong probabilistic primality testing algorithm. On input n, do the following:
| Algorithm P1(n): |
| repeat forever { |
| Generate a random helper string a; |
| Let r = T(n,a); |
| if (r≠ ‘?’) return r; |
| }; |
This algorithm has the property that it might not terminate (in case there are no witnesses to the correct answer for n), but when it does terminate, the answer is correct.
We can trade off the possibility of non-termination for the possibility of failure to find a witness even when one exists. What we do is to add a parameter t which is the maximum number of trials that we are willing to perform. The algorithm then becomes:
| Algorithm P2(n,t): |
| repeat t times { |
| Generate a random helper string a; |
| Let r = T(n,a); |
| if (r≠ ‘?’) return r; |
| } |
| return ‘?’; |
Now the algorithm is allowed to give up and return ‘?’, but only after trying t times to find the correct answer. If there are lots of witnesses to the correct answer, then the probability will be high of finding one, so most of the time the algorithm will succeed.
Unfortunately, we do not know of any test that has lots of witnesses to the correct answer for every n ≥ 2. Fortunately, a weaker test can still be useful.
The tests that we will present are asymmetric. When n is composite, there are many witnesses to that effect, but when n is prime, there are none. Hence, the test either outputs ‘composite’ or ‘?’ but never ‘prime’. We call these weak tests of compositeness since an answer of ‘composite’ means that n is definitely composite, but these tests can never say for sure that n is prime.
When algorithm P2 uses a weak test of compositeness, an answer of ‘composite’ likewise means that n is definitely composite. Moreover, if there are many witnesses to n’s being composite and t is sufficiently large, then the probability that P2(n,t) outputs ‘composite’ will be high. However, if n is prime, then both the test and P2 will always output ‘?’. It is tempting to interpret P2’s output of ‘?’ to mean “n is probably prime”, but of course, it makes no sense to say that n is probably prime; n either is or is not prime. But what does make sense is to say that the probability is very small that P2 answers ‘?’ when n is composite.
In practice, we will indeed interpret the output ‘?’ to mean ‘prime’, but we understand that the algorithm has the possibility of giving the wrong answer when n is composite. Whereas before our algorithm would only report an answer when it was sure and would answer ‘?’ otherwise, now we are considering algorithms that are allowed to make mistakes with (hopefully) small probability.
We can interpret a Boolean function τ(n,a) as a weak test of compositeness by taking an output of true to mean ‘composite’ and an output of false to mean ‘?’. We may also write τa(n) to mean τ(n,a). With this notation, if τa(n) = true, we say that the test τa succeeds on n, and a is a witness to the compositeness of n. If τa(n) = false, then the test fails and gives no information about the compositeness of n. Clearly, if n is prime, then τa fails on n for all a, but if n is composite, then τa may succeed for some values of a and fail for others.
A test of compositeness τ is useful if there is a feasible algorithm that computes τ(n,a), and for every composite number n, a fraction c > 0 of the tests τa succeed on n. Suppose for simplicity that c = 1∕2 and one applies τa to n for 100 randomly-chosen values for a. If any of the τa succeeds, we have a proof a that n is composite. If all fail, we don’t know whether or not n is prime or composite. But we do know that if n is composite, the probability that all 100 tests fail is only 1∕2100.
In practice, we choose RSA primes p and q at random and apply some fixed number of randomly-chosen tests to each candidate,3 rejecting the candidate if it proves to be composite. We keep the candidate (and assume it to be prime) if all of the tests for compositeness fail. We never know whether or not our resulting numbers p and q really are prime, but we can adjust the parameters to reduce the probability to an acceptable level that we will end up a number p or q that is not prime (and hence that we have unwittingly generated a bad RSA key).
Here are two examples of weak tests for compositeness. While neither is useful, they illustrate some of the ideas behind the useful tests that we will present later.
 Z is a valid test of compositeness.
Unfortunately, it isn’t very useful in a probabilistic primality algorithm since the number of
tests that succeed when n is composite are too small. For example, if n = pq for p,q prime,
then the only tests that succeed are δp and δq.
Z is a valid test of compositeness.
Unfortunately, it isn’t very useful in a probabilistic primality algorithm since the number of
tests that succeed when n is composite are too small. For example, if n = pq for p,q prime,
then the only tests that succeed are δp and δq.
 Z is a valid test of compositeness. For this test
to be adequate for a probabilistic primality algorithm, we would need to know that for all
composite numbers n, a significant fraction of the tests ζa succeed on n. Unfortunately, there
are certain compositeness numbers n called pseudoprimes for which all of the tests ζa fail.
Such n are fairly rare, but they do exist. The ζa tests are unable to distinguish pseudoprimes
from true primes, so they are not adequate for testing primality.
Z is a valid test of compositeness. For this test
to be adequate for a probabilistic primality algorithm, we would need to know that for all
composite numbers n, a significant fraction of the tests ζa succeed on n. Unfortunately, there
are certain compositeness numbers n called pseudoprimes for which all of the tests ζa fail.
Such n are fairly rare, but they do exist. The ζa tests are unable to distinguish pseudoprimes
from true primes, so they are not adequate for testing primality.